随机优化(Stochastic Optimization)
在一个充满不确定性(噪声)或者极其复杂(非凸)的环境中,如何利用“随机性”来找到最佳方案。
从确定性优化到随机优化
问题的定义:从确定性世界出发
一切始于一个经典的优化难题。假设我们需要寻找一个系统的最优状态,用数学语言描述就是:
$$\min_{x \in Q} E(x) = m$$其中:
- $x$ 是我们要寻找的参数(比如模型的权重、分子的构型)。
- $E(x)$ 是我们的能量函数(在机器学习中称为损失函数 Loss Function)。我们的目标是让它越小越好。
- $m$ 是理论上的全局最小值。
在确定性优化(Deterministic Method)的世界里,我们通常像瞎子下山一样,沿着梯度的方向一步步挪动。这在简单的地形(凸函数)很有效,但在复杂的现实问题中,我们很容易被困在局部最优的“坑”里出不来。
欢迎来到随机世界 (Welcome to Stochastic World)
为了跳出局部最优的陷阱,我们使用一个关键的转换:我们将“寻找最小能量”的问题,转化为了“寻找最大概率”的问题。
这种转换基于物理学中的 波尔兹曼分布(Boltzmann Distribution)。我们定义一个新的概率密度函数(PDF):
$$f(x) = A e^{-E(x)}$$其中,
- $f(x)$:概率密度函数,必须大于零
- $A = \frac{1}{\int e^{-E(x)} \, dx}$是 归一化常数 (Normalization Constant)
- 在统计物理学中,$A$ 的倒数有一个大名鼎鼎的名字:配分函数 (Partition Function),通常用符号 $Z$ 表示。$$Z = \frac{1}{A} = \int e^{-E(x)} \, dx$$
这里有一个极其巧妙的对应关系:
- $E(x)$ 越小(能量越低,是我们想要的)。
- $e^{-E(x)}$ 就越大。
- 这意味着,$E(x)$ 的 最小值点,恰好对应了概率分布 $f(x)$ 的 峰值(最大值)。
因此,原问题等价转化为:
$$\min E(x) \iff \max f(x)$$为什么要做这个转换?
因为在随机世界里,我们不再执着于“每一步必须往低处走”,而是将解空间看作一个概率场。我们允许算法在一定概率下接受“坏结果”,正是这种机制让我们有机会跳出局部陷阱。
引入温度参数 $\lambda$
为了控制搜索的过程,我们引入一个至关重要的参数 $\lambda$。于是这个概率密度函数就变成了:
$$f(x, \lambda) = A_\lambda e^{-\lambda E(x)}$$其中,$\lambda$ 大于零并与温度 $T$ 成反比:
$$\lambda = \frac{1}{T} \ge 0$$故而,$A$就变成了$A = \frac{1}{\int e^{-\lambda E(x)} \, dx}$
这个 $\lambda$(或 $T$)就像是一个调节器,决定了地形的“分辨率”或“反差”。我们可以通过调节它,来改变概率分布 $f(x, \lambda)$ 的形状。
两个极限状态:探索与锁定
通过分析 $\lambda$ 的极限情况,我们能完美揭示随机优化的运作机制:
状态 A:高温模式 (High Temperature)
当 $\lambda \to 0$ 时(意味着 $T \to \infty$):
- 数学上:$-\lambda E(x) \to 0$,导致 $e^{-\lambda E(x)} \to 1$。
- 结果: $f(x, \lambda) \to \text{Constant}$。
- 物理图景: 此时概率分布在整个空间趋于均匀。无论 $E(x)$ 高低,所有点被采样的概率几乎相等。
- 意义: 这是全图探索 (Exploration) 阶段。算法像气体分子一样在空间中剧烈运动,能够轻松跨越任何高山和深谷,确保我们不会漏掉全局最优解所在的区域。
状态 B:低温模式 (Low Temperature)
当 $\lambda \to \infty$ 时(意味着 $T \to 0$):
- 数学上:差异被无限放大。只要 $E(x)$ 稍微大一点点,$e^{-\lambda E(x)}$ 就会衰减得极快。
- 结果: 概率分布变成了一个尖峰(类似于狄拉克 $\delta$ 函数),仅在能量最低点 $m$ 处有值。
- 物理图景: 系统“冻结”了。
- 意义: 这是精细开发 (Exploitation) 阶段。算法锁定了当前区域的最低点,不再乱跑,从而获得高精度的解。
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation, PillowWriter
# --- 1. 定义能量函数 (Energy Function) ---
# 我们设计一个不对称的双势阱:
# 一个深坑(全局最优),一个浅坑(局部最优)
def energy_function(x):
# (x^2 - 1)^2 是标准的W形双井
# + 0.3*x 用来倾斜它,使左边的坑比右边的深
return (x**2 - 1)**2 + 0.3 * x
# --- 2. 准备数据 ---
x = np.linspace(-2.5, 2.5, 500)
E = energy_function(x)
# 找到真正的全局最小值,用于绘图标记
min_idx = np.argmin(E)
global_min_x = x[min_idx]
global_min_y = E[min_idx]
# --- 3. 设置绘图布局 ---
fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(8, 10), constrained_layout=True)
# 上图:能量景观 E(x) - 永远不变
ax1.plot(x, E, 'k-', linewidth=3, label='Energy $E(x)$')
ax1.scatter(global_min_x, global_min_y, color='gold', s=150, zorder=5, edgecolors='k', label='Global Min')
ax1.set_title("The Problem: Energy Landscape $E(x)$", fontsize=14)
ax1.set_ylabel("Energy")
ax1.grid(True, alpha=0.3)
ax1.legend()
ax1.set_xlim(-2.5, 2.5)
# 下图:概率分布 f(x) - 随温度变化
line, = ax2.plot([], [], 'r-', linewidth=3, alpha=0.8)
fill_poly = ax2.fill_between(x, np.zeros_like(x), np.zeros_like(x), color='red', alpha=0.3)
ax2.set_xlim(-2.5, 2.5)
ax2.set_ylabel("Probability Density $f(x)$")
ax2.set_xlabel("x")
ax2.grid(True, alpha=0.3)
# 动态文本:显示当前的 Lambda 和 Temperature
text_info = ax2.text(0.05, 0.9, '', transform=ax2.transAxes, fontsize=12,
bbox=dict(facecolor='white', alpha=0.8))
# --- 4. 动画逻辑 ---
# Lambda 从 0.1 (高温) 变到 10.0 (低温)
# 我们用对数刻度,让高温阶段展示得慢一点,低温阶段快一点
lambdas = np.logspace(np.log10(0.1), np.log10(15.0), 100)
def init():
line.set_data([], [])
return line,
def update(frame_lambda):
global fill_poly
# === 核心物理计算 ===
# 1. 计算玻尔兹曼因子 (未归一化概率)
# e^(-lambda * E)
unnormalized_prob = np.exp(-frame_lambda * E)
# 2. 计算归一化常数 A (Partition Function Z)
# 利用梯形法则进行数值积分
integral_Z = np.trapezoid(unnormalized_prob, x)
A = 1.0 / integral_Z
# 3. 得到最终概率分布 f(x)
# f(x) = A * e^(-lambda * E)
pdf = A * unnormalized_prob
# =================
# 更新曲线
line.set_data(x, pdf)
# 更新填充区域 (需要移除旧的,画新的)
fill_poly.remove()
fill_poly = ax2.fill_between(x, 0, pdf, color='red', alpha=0.3)
# 动态调整Y轴高度 (因为尖峰会越来越高)
ax2.set_ylim(0, np.max(pdf) * 1.2)
# 更新标题和文字
T = 1 / frame_lambda
ax2.set_title(f"The Stochastic Solution: Probability Distribution", fontsize=14)
text_info.set_text(f"$\lambda$ = {frame_lambda:.2f} (Inverse Temp)\n$T$ = {T:.2f} (Temperature)")
return line, fill_poly, text_info
# --- 5. 生成并保存动画 ---
print("正在生成动画,请稍候...")
ani = FuncAnimation(fig, update, frames=lambdas, init_func=init, blit=False)
# 保存为 GIF (需要安装 imagemagick 或使用 pillow)
ani.save('simulated_annealing.gif', writer=PillowWriter(fps=15))
print("✅ 动画已保存为 'simulated_annealing.gif'")
# 如果在 Jupyter Notebook 中,可以直接解开下面这行注释来显示
#plt.show()
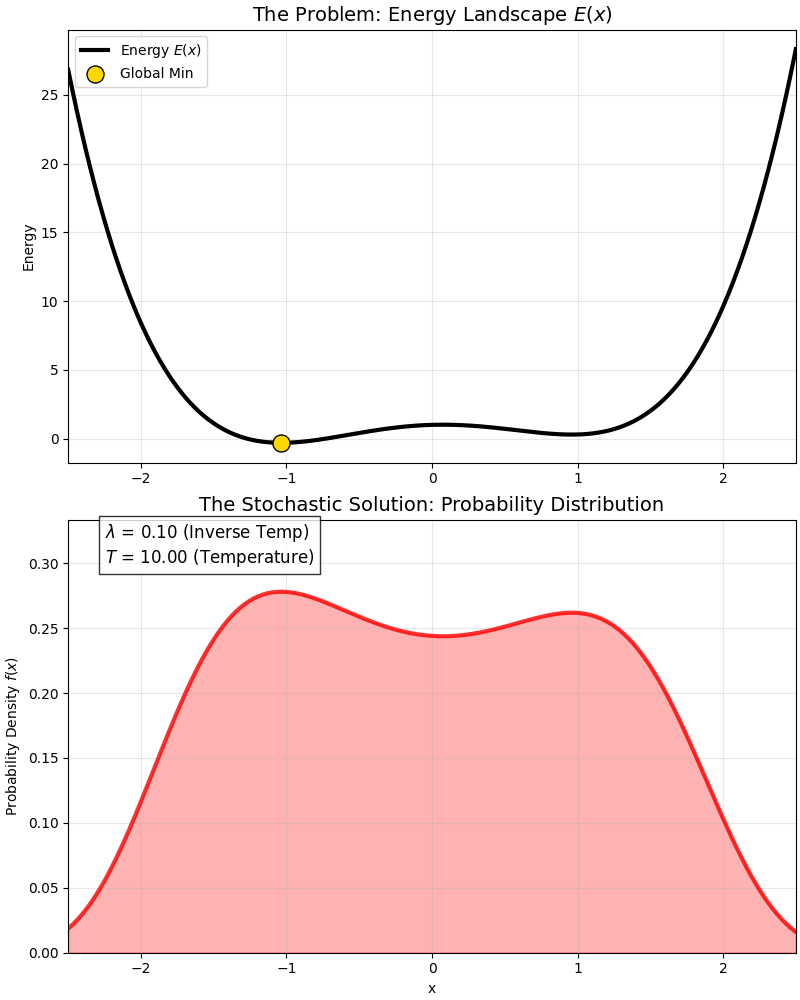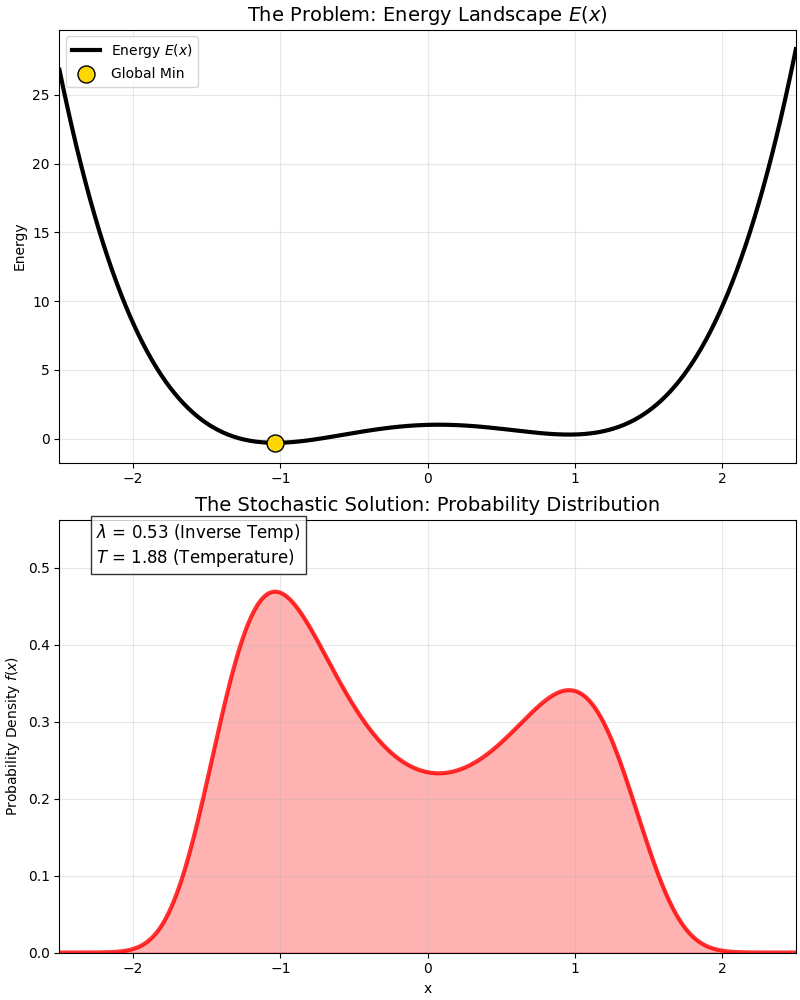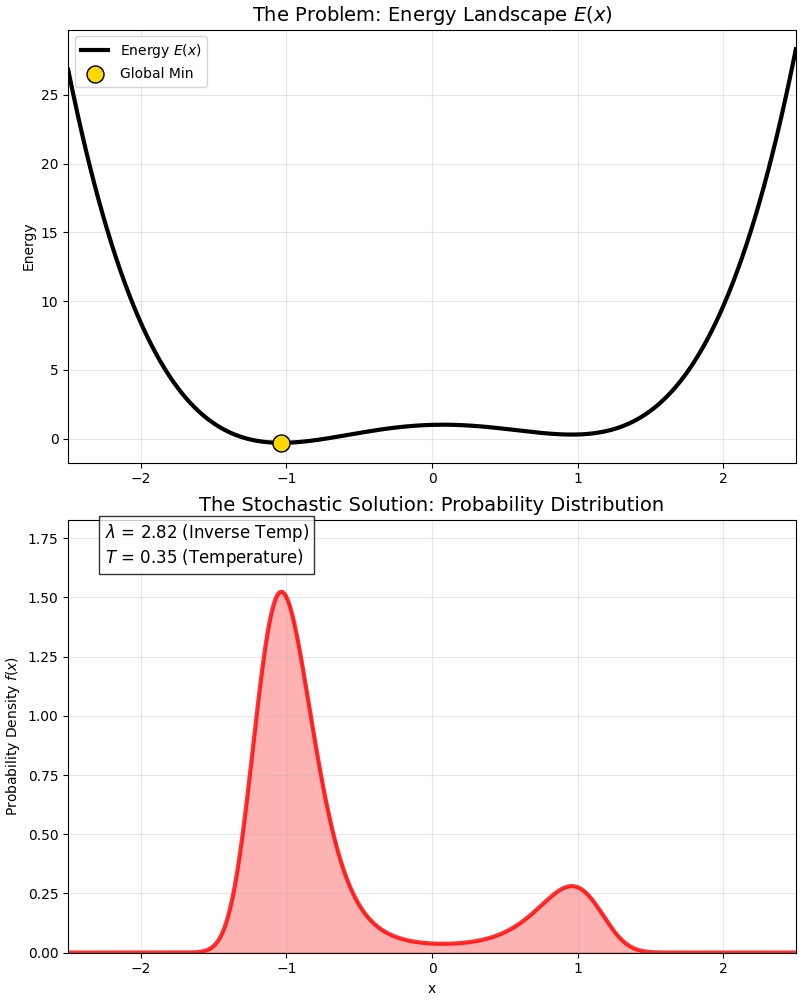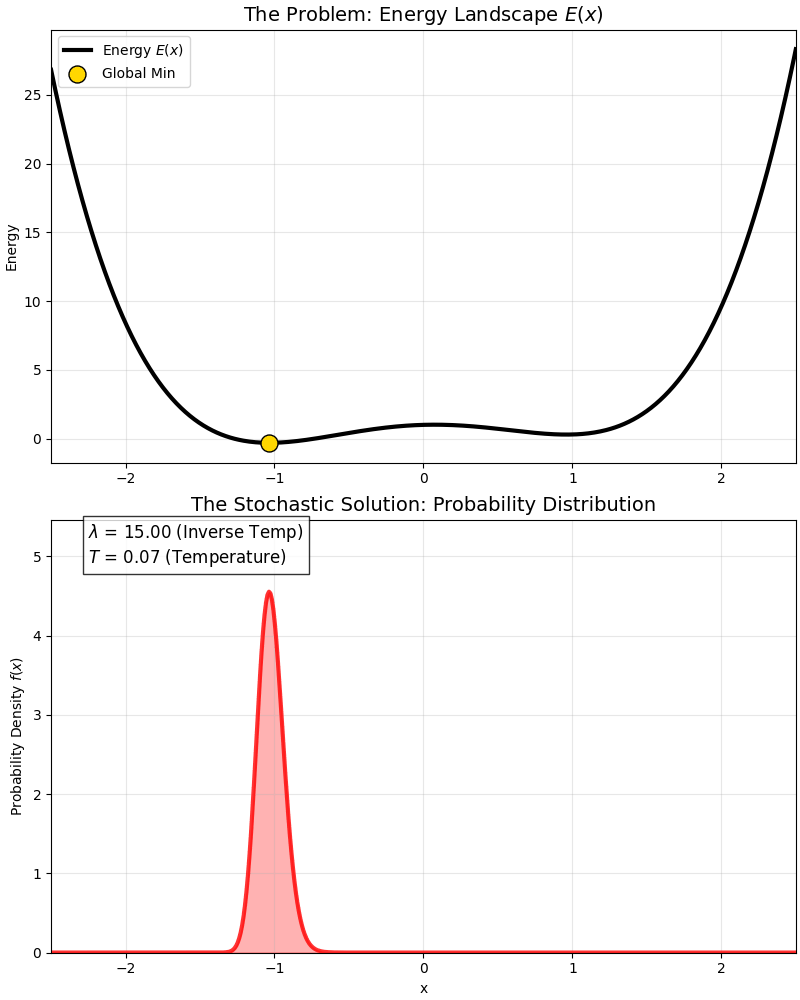
这是一个经典的 “双势阱”(Double Well) 能量函数:
- 它有一个全局最优解(深坑)。
- 还有一个局部最优解(浅坑)。
在高温时,概率分布同时覆盖两个坑(由 $A$ 统管);随着温度降低($\lambda$ 变大),概率分布是如何逐渐“抛弃”局部最优,全部挤到全局最优那个“尖峰”里的。
从 MCMC 到优化——退火的艺术 (The Bridge: Simulated Annealing)
模拟退火 (Simulated Annealing,SA) 是一种通用概率优化算法。
- 名字来源:来自于冶金学中的“退火”工艺。
- 物理退火:把金属加热到很高温(原子乱跑),然后慢慢冷却。这样原子有足够的时间找到能量最低的晶体结构,金属就会变得坚硬且无缺陷。
- 算法退火:把参数 $x$ 扔到很高温(随机乱跑),然后慢慢降低 $T$。这样 $x$ 有足够的时间跳出局部最优,最终落入全局最优。
- 核心特征:它是一种 “允许后悔” 的算法。也就是在搜索过程中,它不仅接受“好”的解,也会以一定概率接受“坏”的解(为了跳出坑)。
之前提到的的 Steepest Descent (梯度下降) 是个“势利眼”,只往低处走。如果地形是像 鸡蛋托盘 那样的(无数个小坑),梯度下降掉进第一个坑就死在那里了。
而 SA 的优势在于:
- 全局搜索能力:因为它在高温时接受“坏解”,所以它能爬坡翻越山岭,去探索未知的领域。
- 不依赖梯度:它不需要求导($f(x)$ 甚至可以是不连续的)。
- 万金油:不管函数长多丑,只要你能算出函数值,它就能跑。
- 无论$f(x)$是否凸,都能应用
算法流程
- 定义转换 (Transform): 我们不直接去解 $\min E(x)$,而是构建一个概率分布:$$f(x) \propto e^{-E(x)/T}$$
- 这里 $\lambda = 1/T$
- 直觉:把“地形高度”变成“概率密度”。坑越深($E$ 越小),概率越大;山越高($E$ 越大),概率越小。
- 高温探索 (Explore) (高温采样):
- 操作:设置一个很高的初始温度 $T_{max}$。
- 现象:
- 当 $T$ 很大时,$E(x)/T \approx 0$,所以 $e^0 \approx 1$。
- 整个概率分布是扁平的(Flat),接近均衡分布。
- 这时候你丢下去的“粒子”(采样点)会满地图乱跑(因为去到哪里的概率基本一致),可以轻易翻过高山,跳出局部陷阱。
- 降温过程 (Cooling / Annealing): 慢慢降低温度 $T$(增大 $\lambda$)。
- 操作:按照一个时间表逐渐降低 $T$。
- 例如:$T(t) \sim \frac{c}{\log(1+t)}$
- 这是一个非常著名的理论公式(Geman & Geman, 1984),保证能找到全局最优,但它降温极慢。
- 实际工程中,我们通常用更快的方法,比如 $T_{new} = T_{old} \times 0.99$。
- 例如:$T(t) \sim \frac{c}{\log(1+t)}$
- 现象:随着温度降低,分布图开始“变形”。原本平坦的地方变低,原本深坑的地方变得更深(概率峰值更尖)。
- 操作:按照一个时间表逐渐降低 $T$。
- 低温开发 (Exploit) :持续采样 (Loop till Low T)
- 操作:继续循环“采样 -> 降温 -> 采样”,直到温度 $T$ 非常低
- ⚠️ 但不能等于 0,否则除数无意义。
- 现象:此时概率分布已经变成了一根针(Dirac Delta)。粒子基本被“锁死”在那个最深的坑里,很难再跳出来了。
- 操作:继续循环“采样 -> 降温 -> 采样”,直到温度 $T$ 非常低
- 均值估算 (Sample & Average)
- 操作:在低温阶段采集一堆样本 $x_1, x_2, ..., x_n$,算出它们的平均值。
- 结论:这个平均值 $\bar{x}$ 就是我们估计的全局最小值位置 $x_{min}$。
注意:
- 刚开始 $T$ 很大,$\Delta E / T$ 很小,$P$ 接近 1。算法几乎接受所有坏解(疯狂乱跑)。
- 后来 $T$ 很小,$\Delta E / T$ 很大,$P$ 接近 0。算法几乎拒绝所有坏解(变成了梯度下降)。
示例
一维
这里使用一个有多处陷阱的函数来展示“温度控制”和“Metropolis采样”的结合:$E(x) = x^2 - \cos(\pi x)$。
import numpy as np
import matplotlib.pyplot as plt
# --- 1. 目标函数 (Energy Function) ---
def E(x):
return x**2 - np.cos(np.pi * x)
# --- 2. 采样核心: Metropolis 准则 ---
# 这是一个"抽样机",负责根据当前温度 T 生成样本
def sample_one_step(x_curr, T):
# a. 提议 (Propose): 随机往左或往右迈一步
x_next = x_curr + np.random.uniform(-0.5, 0.5)
# b. 能量差 (Delta E)
dE = E(x_next) - E(x_curr)
# c. 接受/拒绝 (Accept/Reject)
# 核心逻辑:如果新位置能量低,一定去;如果高,有一定概率去(取决于温度T)
if dE < 0 or np.random.rand() < np.exp(-dE / T):
return x_next # 接受移动
else:
return x_curr # 拒绝移动,待在原地
# --- 主流程: 对应你的笔记步骤 ---
def run_stochastic_optimization():
# 初始化
x = -2.5 # 起点 (故意选在一个较远的局部最优附近)
T = 10.0 # T_max (高温)
T_min = 0.01 # T_min (低温截止)
alpha = 0.99 # 降温系数 (实际常用的降温方式)
path = [] # 记录走过的路径
temps = [] # 记录温度变化
print(f"{'Step':<6} | {'Temp':<8} | {'Current x':<10} | {'Action'}")
print("-" * 45)
step = 0
# 流程 4: 直到温度非常低 (Till a very low T)
while T > T_min:
# 流程 2 & 3: 采样 并 降温
x = sample_one_step(x, T)
# 记录数据
path.append(x)
temps.append(T)
# 打印中间过程 (每隔200步)
if step % 200 == 0:
status = "Explore 🎲" if T > 1.0 else "Exploit 🎯"
print(f"{step:<6} | {T:<8.4f} | {x:<10.4f} | {status}")
# 降温 (Decrease T)
T = T * alpha
step += 1
# 流程 5: 统计均值 (Avg Samples)
# 取最后 100 个低温样本的均值
final_samples = path[-100:]
estimated_min = np.mean(final_samples)
print("-" * 45)
print(f"✅ 最终估算结果: x = {estimated_min:.4f}")
print(f"✅ 真实最小值: x = 0.0000 (大概率重合)")
return path, temps
# --- 运行并可视化 ---
path, temps = run_stochastic_optimization()
# 画图展示粒子是如何"从乱跑"到"归位"的
plt.figure(figsize=(10, 6))
plt.plot(path, alpha=0.6, label='Particle Path')
plt.xlabel('Iterations (Time)')
plt.ylabel('Position x')
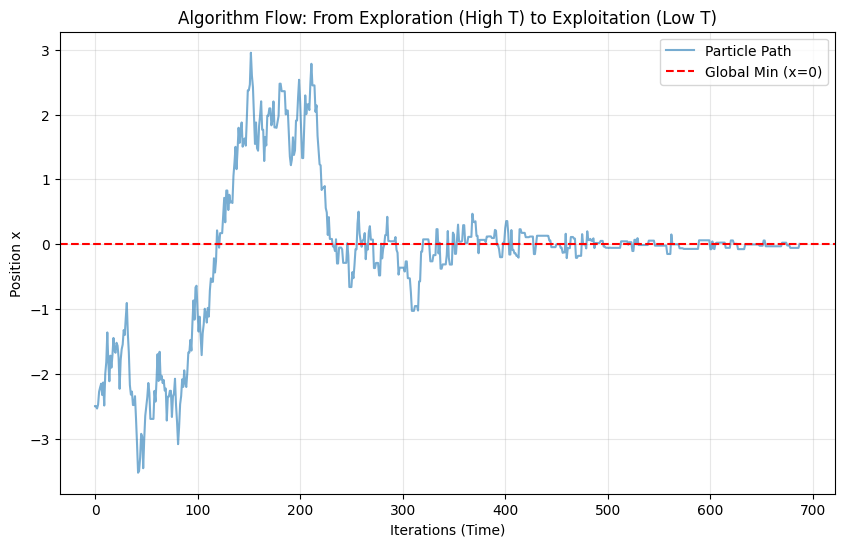
plt.title('Algorithm Flow: From Exploration (High T) to Exploitation (Low T)')
plt.axhline(0, color='r', linestyle='--', label='Global Min (x=0)')
plt.grid(True, alpha=0.3)
plt.legend()
plt.show()
Step | Temp | Current x | Action
---------------------------------------------
0 | 10.0000 | -2.5000 | Explore 🎲
200 | 1.3398 | 2.2058 | Explore 🎲
400 | 0.1795 | 0.2473 | Exploit 🎯
600 | 0.0241 | -0.0782 | Exploit 🎯
---------------------------------------------
✅ 最终估算结果: x = -0.0115
✅ 真实最小值: x = 0.0000 (大概率重合)
上面生成的图
- 前半段 (左边):曲线震荡非常剧烈。这就是高温探索,粒子根本不在乎那里是坑,它在整个区域乱跳。
- 后半段 (右边):曲线变成了一条直线。这就是低温锁定,粒子被困在了 $x=0$ 附近。
- 结果:最后我们把后半段那些“静止”的点取平均,就得到了精准的最小值。
N 维
为了演示 N 维的挑战性,我们选用著名的 Rastrigin 函数。这是一个“恶名昭彰”的测试函数:它就像一个布满鸡蛋托盘的大碗,宏观上看是个碗(有全局最优),但微观上到处都是坑(局部最优)。
N 维 Rastrigin 函数定义公式如下($A=10$):
$$f(\mathbf{x}) = 10n + \sum_{i=1}^n (x_i^2 - 10 \cos(2\pi x_i))$$它的全局最小值在原点 $\mathbf{x} = [0, 0, \dots, 0]$,函数值为 0。
import numpy as np
import matplotlib.pyplot as plt
# --- 1. 定义 N 维目标函数 (Rastrigin Function) ---
def rastrigin(x):
# x 是一个向量 (numpy array)
# A * n + sum(x^2 - A * cos(2*pi*x))
A = 10
n = len(x)
return A * n + np.sum(x**2 - A * np.cos(2 * np.pi * x))
# --- 2. N 维邻域生成 (Proposal) ---
def get_neighbor(x_curr, step_size=0.5):
# 关键点:我们在 N 维空间中随机游走
# size=len(x_curr) 保证了生成的扰动向量和 x 维度一致
perturbation = np.random.uniform(-step_size, step_size, size=len(x_curr))
return x_curr + perturbation
# --- 3. 模拟退火主程序 ---
def simulated_annealing_nd(n_dim=2, n_iter=2000):
# 初始化:在一个范围内随机生成起点 (-5.12 到 5.12 是 Rastrigin 的标准定义域)
current_x = np.random.uniform(-5.12, 5.12, size=n_dim)
current_E = rastrigin(current_x)
# 记录最佳解 (Best So Far),防止跑丢了
best_x = current_x.copy()
best_E = current_E
# 温度设置
T = 100.0
T_min = 1e-4
alpha = 0.99 # 降温系数
path = [current_x] # 记录路径用于画图
energy_history = [current_E]
print(f"开始 {n_dim} 维优化...")
print(f"起点: {np.round(current_x, 2)}, Energy: {current_E:.2f}")
iter_count = 0
while T > T_min and iter_count < n_iter:
# 1. 提议新位置 (向量加法)
new_x = get_neighbor(current_x)
# 防止跑出定义域 (Rastrigin 通常限制在 [-5.12, 5.12])
new_x = np.clip(new_x, -5.12, 5.12)
new_E = rastrigin(new_x)
# 2. 计算能量差
dE = new_E - current_E
# 3. Metropolis 准则 (和 1 维一模一样)
if dE < 0 or np.random.rand() < np.exp(-dE / T):
current_x = new_x
current_E = new_E
# 更新历史最佳
if current_E < best_E:
best_x = current_x.copy()
best_E = current_E
path.append(current_x)
energy_history.append(current_E)
T *= alpha
iter_count += 1
print(f"结束. 最终位置: {np.round(best_x, 4)}")
print(f"最终能量: {best_E:.6f} (理论最优是 0.0)")
return np.array(path), energy_history, best_x
# --- 运行: 这里我们设为 2 维以便画图,但算法支持 N 维 ---
DIMENSION = 2
path, energies, final_sol = simulated_annealing_nd(n_dim=DIMENSION, n_iter=3000)
# --- 4. 可视化 (仅适用于 2D) ---
if DIMENSION == 2:
plt.figure(figsize=(12, 5))
# 子图 1: 地形图和路径
plt.subplot(1, 2, 1)
x_grid = np.linspace(-5.12, 5.12, 100)
y_grid = np.linspace(-5.12, 5.12, 100)
X, Y = np.meshgrid(x_grid, y_grid)
# 计算网格上每个点的 Z 值
Z = np.zeros_like(X)
for i in range(X.shape[0]):
for j in range(X.shape[1]):
Z[i,j] = rastrigin(np.array([X[i,j], Y[i,j]]))
plt.contourf(X, Y, Z, levels=50, cmap='viridis', alpha=0.7)
plt.colorbar(label='Energy')
# 画路径:起点是白色,终点是红色
plt.plot(path[:, 0], path[:, 1], 'w-', linewidth=0.5, alpha=0.6)
plt.scatter(path[0, 0], path[0, 1], c='white', s=50, label='Start')
plt.scatter(final_sol[0], final_sol[1], c='red', marker='*', s=200, label='End')
plt.legend()
plt.title(f"2D Rastrigin Optimization Path\n(Escaping many local minima)")
# 子图 2: 能量下降曲线
plt.subplot(1, 2, 2)
plt.plot(energies)
plt.yscale('log') # 用对数坐标看,因为后期下降很微小
plt.xlabel('Iteration')
plt.ylabel('Energy (Log Scale)')
plt.title('Energy Minimization Process')
plt.grid(True, which="both", ls="--")
plt.tight_layout()
plt.show()
开始 2 维优化...
起点: [-0.04 4.85], Energy: 28.08
结束. 最终位置: [1.0266 2.0164]
最终能量: 5.312337 (理论最优是 0.0)
- 代码中的关键行:
perturbation = np.random.uniform(-step_size, step_size, size=len(x_curr))这就是 N 维扩展的核心。我们一次性生成了一个 N 维的随机向量。- 在数学上,这相当于在 N 维超球体(或超立方体)中随机选一个方向跳出去。
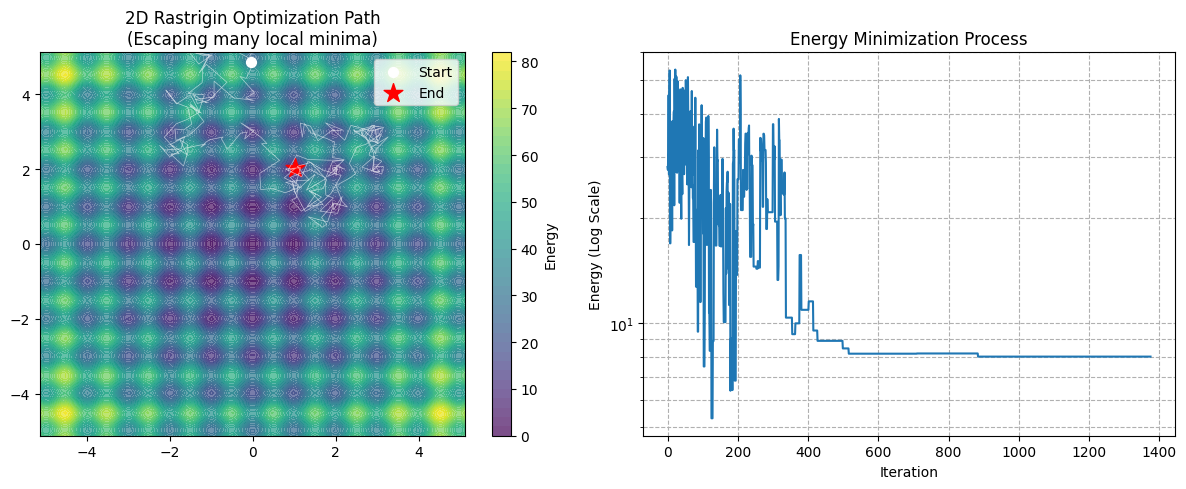
- Rastrigin 的地形 (左图):你会看到有很多深蓝色的圈圈,每一个都是一个局部陷阱。
- 如果是 梯度下降(Gradient Descent):它大概率会掉进离起点最近的那个蓝色圈圈里,然后死在那里。
- 模拟退火:你会看到白色的路径在图上乱窜(特别是前期)。它会跳进一个坑,跳出来,再跳进另一个坑,直到温度降低,被“吸”进最中间那个最深的坑(红色五角星)。
- Pincus Theorem 在 N 维的意义:即使是 N 维,Pincus Theorem 依然成立:$$\lim_{\lambda \to \infty} \frac{\int_{\mathbb{R}^N} \mathbf{x} e^{-\lambda E(\mathbf{x})} d\mathbf{x}}{\int_{\mathbb{R}^N} e^{-\lambda E(\mathbf{x})} d\mathbf{x}} = \mathbf{x}_{min}$$
- 这说明无论维度多高,只要我们能通过降温过程正确地从那个 N 维概率分布中采样,均值(或最后停留的位置)依然是全局最优。
证明退火算法的正确性:Pincus Theorem
Pincus Theorem 为模拟退火算法提供了收敛性的理论保证(Theoretical Guarantee)。 Pincus Theorem 证明了“如果温度降到 0,这一堆样本的平均值就是全局最优解”; 模拟退火算法则负责“如何安全、平稳地把温度降到 0,而不让样本卡在半路”。
Pincus Theorem (1968年由 Mark Pincus 提出)
Pincus Theorem 是一个数学桥梁,它证明了:当我们把温度降到极低($\lambda \to \infty$)时,一个函数的“加权平均值”(期望),就会收敛于这个函数的“全局最小值点”。
它把一个 “寻找极值的问题”(Optimization)变成了一个“计算积分的问题”(Integration)。
假设你有一个目标函数 $f(x)$,定义域为 $D$,你想要找到它的全局最小值点 $x^*$。Pincus Theorem 指出:
$$x^* = \lim_{\lambda \to \infty} \frac{\int_D x \cdot e^{-\lambda f(x)} \, dx}{\int_D e^{-\lambda f(x)} \, dx}$$或者写成统计学的期望形式:
$$x^* = \lim_{\lambda \to \infty} \mathbb{E}_{\lambda}[x]$$其中 $\lambda$ 是一个参数(对应物理中的 $1/T$)。
证明
我们的目标是求这个分式的极限:
$$\langle x \rangle_\lambda = \frac{\int x \cdot e^{-\lambda E(x)} \, dx}{\int e^{-\lambda E(x)} \, dx}$$我们要证明:当 $\lambda \to \infty$ 时,这个结果等于 $x^*$(即 $E(x)$ 的全局最小值点)。
关键技巧:既然 $\lambda$ 很大,为了看清谁在主导,我们把分子和分母同时提取出那个“最大的项”。
第一步:提取“最大公约数”
假设 $x^*$ 是唯一的全局最小值点。那么对于任何 $x \neq x^*$,都有 $E(x) > E(x^*)$。
我们在分子和分母中,同时提出 $e^{-\lambda E(x^*)}$ 这一项:
- 分母:$$\int e^{-\lambda E(x)} \, dx = \int e^{-\lambda [E(x^*) + (E(x) - E(x^*))]} \, dx = e^{-\lambda E(x^*)} \int e^{-\lambda (E(x) - E(x^*))} \, dx$$
- 分子:$$\int x e^{-\lambda E(x)} \, dx = e^{-\lambda E(x^*)} \int x \cdot e^{-\lambda (E(x) - E(x^*))} \, dx$$
把它代回原式,你会发现 $e^{-\lambda E(x^*)}$ 在分子分母中约分消掉了!
$$\langle x \rangle_\lambda = \frac{\int x \cdot e^{-\lambda (E(x) - E(x^*))} \, dx}{\int e^{-\lambda (E(x) - E(x^*))} \, dx}$$这一步非常关键。现在积分里的指数变成了 $-\lambda (E(x) - E(x^*))$。注意括号里的 $\Delta E = E(x) - E(x^*)$ 永远是大于等于 0 的。
第二步:切分积分区域 (邻域 vs. 远方)
现在我们把积分区域分成两部分:
- 极小值附近的小邻域 $U_\epsilon$: $|x - x^*| < \epsilon$(这里 $\epsilon$ 是个很小的数)。
- 其余区域 $R$:远离最小值的地方。
让我们看看当 $\lambda \to \infty$ 时,这两部分分别发生了什么。
- 分析“其余区域 R”(远离最小值的地方):在这些地方,$\Delta E = E(x) - E(x^*)$ 肯定有一个大于 0 的最小值,设为 $\delta > 0$。那么指数项 $e^{-\lambda \Delta E} \le e^{-\lambda \delta}$。当 $\lambda \to \infty$ 时,这一项会以指数级速度衰减到 0。这意味着:在极限情况下,所有远离 $x^*$ 的区域,对积分的贡献都可以忽略不计。
- 分析“邻域 $U_\epsilon$”(极小值附近):在这个微小的区域里,$\Delta E \approx 0$,所以 $e^{-\lambda \Delta E} \approx 1$(或者衰减得很慢)。整个积分的值,完全由这一小块区域主导。
第三步:局部泰勒展开 (Taylor Expansion)
为了更精确,我们在 $x^*$ 附近对 $E(x)$ 做泰勒展开:
$$E(x) \approx E(x^*) + E'(x^*)(x-x^*) + \frac{1}{2}E''(x^*)(x-x^*)^2$$因为 $x^*$ 是极值点,一阶导数 $E'(x^*) = 0$。且假设它是极小值,二阶导数 $E''(x^*) = k > 0$。所以:
$$E(x) - E(x^*) \approx \frac{1}{2} k (x-x^*)^2$$代入我们的积分式(只看邻域部分):
$$\text{分母} \approx \int_{x^*-\epsilon}^{x^*+\epsilon} e^{-\lambda \frac{1}{2} k (x-x^*)^2} \, dx$$看!这变成了一个标准的高斯积分 (Gaussian Integral)。如果你还记得高斯积分公式 $\int e^{-ax^2} dx = \sqrt{\frac{\pi}{a}}$,那这里 $a = \frac{\lambda k}{2}$。
所以分母大约是:
$$\text{分母} \approx \sqrt{\frac{2\pi}{\lambda k}}$$同理,分子由两部分组成:$x$ 和高斯分布。因为积分范围非常小(在 $x^*$ 附近),我们可以把 $x$ 近似看作常数 $x^*$ 提出来:
$$ \text{分子} \approx \int_{x^*-\epsilon}^{x^*+\epsilon} x \cdot e^{-\lambda \frac{1}{2} k (x-x^*)^2} \, dx \approx x^* \cdot \underbrace{\int e^{-\dots} dx}_{\text{分母的积分}} $$$$ \text{分子} \approx x^* \cdot \sqrt{\frac{2\pi}{\lambda k}} $$第四步:见证奇迹的约分
现在我们把分子分母重新放在一起:
$$\lim_{\lambda \to \infty} \langle x \rangle_\lambda \approx \frac{x^* \cdot \sqrt{\frac{2\pi}{\lambda k}}}{\sqrt{\frac{2\pi}{\lambda k}}}$$那堆复杂的根号、$\pi$、二阶导数 $k$、甚至 $\lambda$ 本身,全部在分子分母中抵消了!最后剩下的只有:
$$= x^*$$
Scan to Share
微信扫一扫分享