随机变量(Random Variables)
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
# 设置样式
sns.set_theme(style="whitegrid")
def plot_discrete_rv(values, pmf, cdf, samples, rv_name):
# 准备经验 CDF(ECDF)
n_samples = len(samples)
sorted_samples = np.sort(samples)
ecdf_x = np.unique(sorted_samples)
ecdf_y = [np.sum(sorted_samples <= x) / n_samples for x in ecdf_x]
plt.figure(figsize=(15, 8))
# 理论 PMF
plt.subplot(2, 2, 1)
plt.stem(values, pmf, basefmt=" ", linefmt='-.')
plt.title(f"Theoretical PMF: {rv_name}")
plt.xlabel("x")
plt.ylabel("f(X=x) = P(X = x)")
plt.ylim(0, 1.1)
# 理论 CDF
plt.subplot(2, 2, 2)
plt.step(values, cdf, where='post', color='green')
plt.title(f"Theoretical CDF: {rv_name}")
plt.xlabel("x")
plt.ylabel("F(x) = P(X ≤ x)")
plt.ylim(0, 1.1)
plt.grid(True)
# 采样直方图
plt.subplot(2, 2, 3)
sns.countplot(x=samples, hue=samples, legend=False, palette='pastel', stat='proportion', order=values)
plt.title(f"Empirical Distribution ({n_samples} samples)")
plt.xlabel("x")
plt.ylabel("Relative Frequency")
# 经验 CDF(ECDF)
plt.subplot(2, 2, 4)
plt.step(ecdf_x, ecdf_y, where='post', color='orange')
plt.title("Empirical CDF")
plt.xlabel("x")
plt.ylabel("ECDF")
plt.ylim(0, 1.1)
plt.grid(True)
plt.tight_layout()
plt.show()
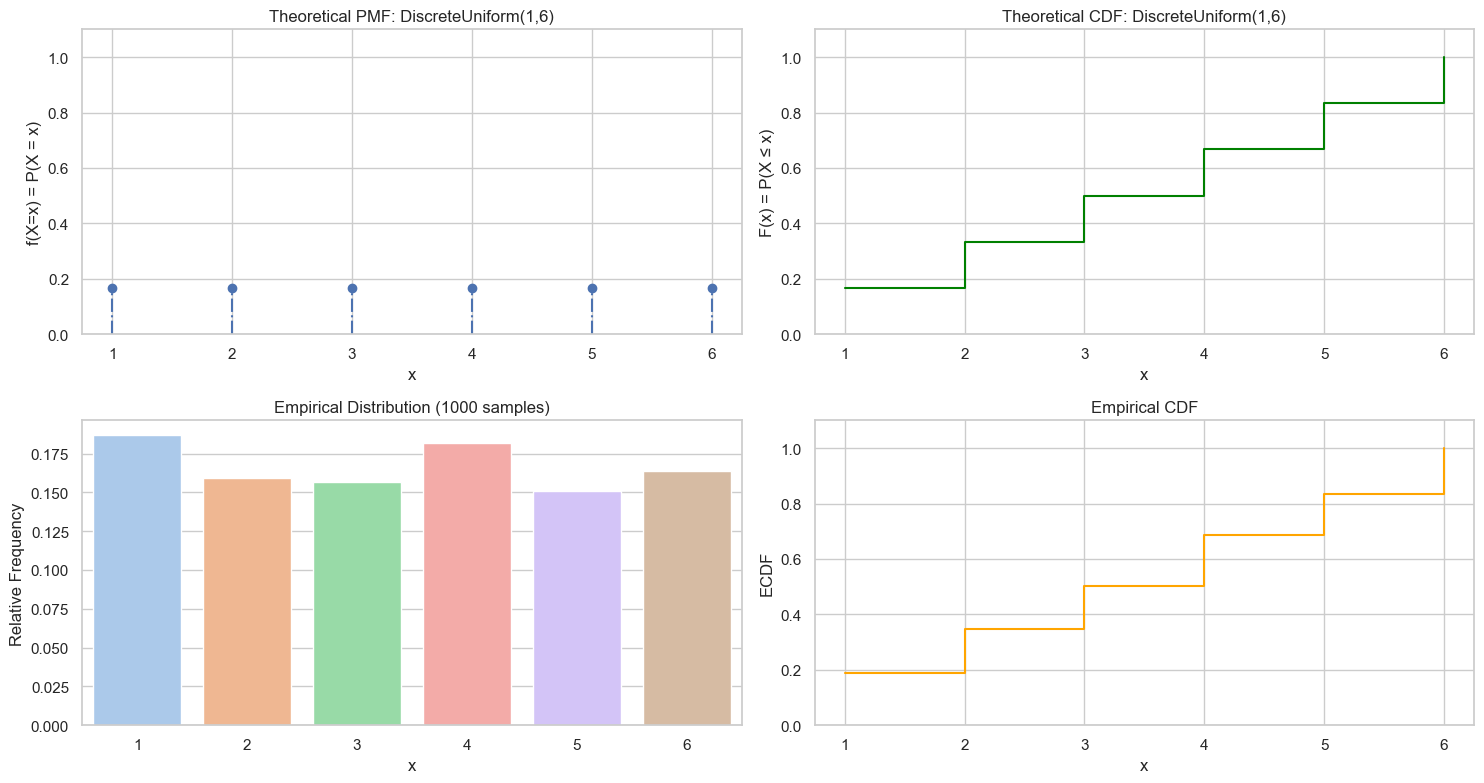
均匀分布(Uniform RV)
离散均匀分布(Discrete Uniform Random Variable)
如果一个随机变量 $X$ 在一组有限的离散数值集合中取值,且每个值出现的概率相同,那么它就是一个离散型均匀随机变量。
示例:
- 掷一个骰子: $X \in \{1, 2, 3, 4, 5, 6\}$,每个点的概率是 $\frac{1}{6}$
- 随机选择一张扑克牌(从 1 到 52)
数学定义
设 $X \sim \text{DiscreteUniform}(a, b)$,其中 $a$, $b \in \mathbb{Z}$,且 $a \leq b$。
支持集(取值范围,值域)是:
$$ k \in \{a, a+1, a+2, \dots, b\} $$每个值的概率是:
$$ P(X = k) = \frac{1}{b - a + 1}, \quad \text{for } k \in \{a, \dots, b\} $$概率质量函数(PMF):
$$ f(X=k) = P(X=k) = \left\{ \begin{aligned} \frac{1}{b-a+1}, \text{for } a \le k \le b\\ 0, \text{ otherwise} \end{aligned} \right. $$累积分布函数(CDF):
$$ F(X=k) = P(X\le k) = \left\{ \begin{aligned} 0, \text{for } k \lt a \\ \frac{k-a+1}{b-a+1}, \text{for } a \le k \le b\\ 1, \text{ for } k \gt b \end{aligned} \right. $$期望($\mu$):$\frac{a+b}{2}$
方差($\sigma^2$):$\frac{(b-a+1)^2-1}{12}$
import numpy as np
# 设置随机种子以保证结果可重复
np.random.seed(42)
# 1. 定义参数
a, b = 1, 6 # 均匀分布的范围
values = np.arange(a, b+1) # 离散取值:1~6
n = len(values)
pmf = np.ones(n) / n # 每个值的概率均等
cdf = np.cumsum(pmf) # 累积分布函数
# 2. 抽样
n_samples = 1000
samples = np.random.choice(values, size=n_samples, p=pmf)
# 3. 可视化:理论分布 + 采样频率对比
plot_discrete_rv(values, pmf, cdf, samples, f"DiscreteUniform({a},{b})")
采样
我们使用一个连续均匀分布 $U \sim \text{Uniform}(0, 1)$ 来生成离散均匀随机数。
步骤:
设区间为整数 $a$ 到 $b$(含端点),总共有 $N = b - a + 1$ 个数
生成一个随机数 $U \sim \text{Uniform}(0, 1)$
将 $U$ 映射到整数范围内:
$$ X = a + \left\lfloor U \cdot N \right\rfloor $$✅ 这样得到的整数就是 $\{a, a+1, ..., b\}$ 中的一个,且等概率
如果 $a=0, b=1$,则:
- $N = b - a + 1 = 1 - 0 + 1 = 2$
- $U \sim \text{Uniform}(0, 1)$
- $X = a + \left\lfloor U \cdot N \right\rfloor = 0 + \left\lfloor U \cdot 2 \right\rfloor = \left\lfloor U \cdot 2 \right\rfloor$
总结:
| 步骤 | 描述 |
|---|---|
| 目标 | 从 $\{a, a+1, ..., b\}$ 中等概率采样 |
| 方法 | 生成 $U \sim \text{Uniform}(0,1)$,然后 $X = a + \lfloor U \cdot (b - a + 1) \rfloor$ |
| 工具函数 | random.random() or random.randint(a, b) |
| 应用 | 模拟骰子、轮盘、抽签、均匀整数采样等 |
import random
def discrete_uniform_sample(a, b, n):
N = b - a + 1
# U ~ Uniform(0, 1)
U = [random.random() for _ in range(n)] # random.random() 返回区间 [0.0, 1.0) 的浮点数
# X ~ Discrete Uniform(a, b)
X = [a+int(u*N) for u in U] # When u = 0.999, u*N = 0.999 * N, which is close to N-1, so a + int(u*N) will be b.
return U, X
discrete_uniform_sample(0, 1, 10)
([0.4444854289944321,
0.951251619861675,
0.7646892516581814,
0.9854176841589392,
0.0983350059391166,
0.5245935455925463,
0.962496892423623,
0.7602027193895072,
0.3724452123714195,
0.8460390235179297],
[0, 1, 1, 1, 0, 1, 1, 1, 0, 1])
更简洁方式(内置函数)
当然,Python 也提供了直接采样的方法:random.randint(a, b) # 包含 a 和 b
它实现的就是上面的原理。
[random.randint(0, 1) for _ in range(10)] # 使用内置函数直接采样,验证结果是否正确
[0, 1, 1, 0, 0, 1, 0, 0, 0, 0]
验证采样结果
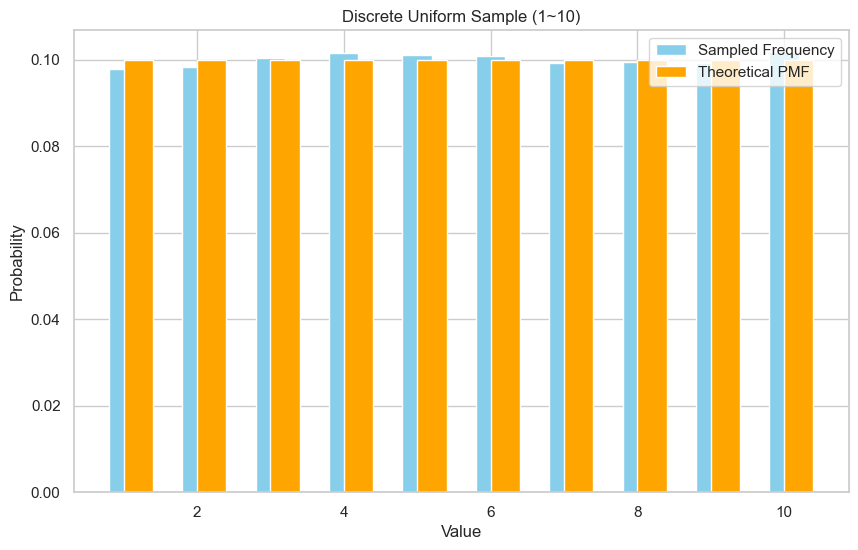
我们采样 10,000 次,看看分布是否均匀。
你会看到 1 到 6 之间的柱状图高度大致相等,这说明我们正确采样。
import random
import matplotlib.pyplot as plt
from math import comb
# 采样
a, b, N = 1, 10, 30000
origin_samples, samples = discrete_uniform_sample(a, b, N)
print(f"Empirical mean: {sum(samples)/len(samples):.3f}")
# 统计频率
counts = [samples.count(k) / N for k in range(a, b+1)]
# 计算理论概率(PMF)
theoretical = [1/(b-a+1) for _ in range(a, b+1)]
print(f"PMF = {theoretical}")
# Step 5: 可视化
plt.figure(figsize=(10, 6))
plt.bar(range(a, b+1), counts, width=0.4, label='Sampled Frequency', color='skyblue', align='center')
plt.bar(range(a, b+1), theoretical, width=0.4, label='Theoretical PMF', color='orange', align='edge')
plt.xlabel("Value")
plt.ylabel("Probability")
plt.title(f"Discrete Uniform Sample ({a}~{b})")
plt.legend()
plt.grid(True)
plt.show()
Empirical mean: 5.515
PMF = [0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1]
连续均匀分布(Continuous Uniform Random Variable)
什么是连续型均匀分布?
一个随机变量 $X \sim \text{Uniform}(a, b)$,如果它在区间 $[a, b]$ 上的每一个值都等可能地出现,那么我们称它服从连续均匀分布。
数学定义
支持集(取值范围):$X \in [a, b]$
概率密度函数(PDF):
$$ f_X(x) = \begin{cases} \frac{1}{b - a} & \text{if } x \in [a, b] \\ 0 & \text{otherwise} \end{cases} $$累积分布函数(CDF):
$$ F_X(x) = \begin{cases} 0 & \text{if } x < a \\ \frac{x - a}{b - a} & \text{if } a \leq x \leq b \\ 1 & \text{if } x > b \end{cases} $$期望($\mu$):$\frac{a+b}{2}$
方差($\sigma^2$):$\frac{(b-a)^2}{12}$
参考:
采样
采样原理(Inverse Transform Sampling)
最简单有效的方法是:
如果 $U \sim \text{Uniform}(0,1)$,那么
$$ > X = a + (b - a) \cdot U \sim \text{Uniform}(a, b) > $$
💡为什么成立?
因为:
- $U \in [0, 1]$,是标准均匀分布
- 缩放区间长度为 $(b - a)$,再加上 $a$ 相当于“线性映射”
- 变换后的随机变量 $X$ 在 $[a, b]$ 上也均匀分布
采样步骤:
Step 1:生成一个 U ~ Uniform(0, 1)
Step 2:通过线性变换 X = a + (b - a) * U
Step 3:X 就是你要的 sample from Uniform(a, b)
总结表格
| 项目 | 内容 |
|---|---|
| 分布名称 | 连续均匀分布 Uniform(a, b) |
| $f(x) = \frac{1}{b - a}$ | |
| 采样方法 | $X = a + (b - a) \cdot U$,其中 $U \sim \text{Uniform}(0,1)$ |
| Python函数 | random.random() 或 random.uniform(a, b) |
| 应用场景 | 蒙特卡洛方法、模拟实验、随机初始化等 |
import random
def sample_uniform(a, b):
U = random.random() # U ~ Uniform(0,1)
X = a + (b - a) * U # X ~ Uniform(a, b)
return X
def sample_uniform_list(a, b, n):
return [sample_uniform(a, b) for _ in range(n)]
sample_uniform_list(0, 1, 10)
[0.6400024988096578,
0.05979675338996093,
0.5161926269415474,
0.4823864030690008,
0.31338893853775884,
0.4885049387562129,
0.7751242044584421,
0.03653104468277457,
0.1006986841203773,
0.05647975387925808]
直接用内置函数 uniform(a, b)
这是标准库封装好的形式,内部实现其实也是 a + (b - a) * random.random()。
random.uniform(0, 1)
0.8338807889744516
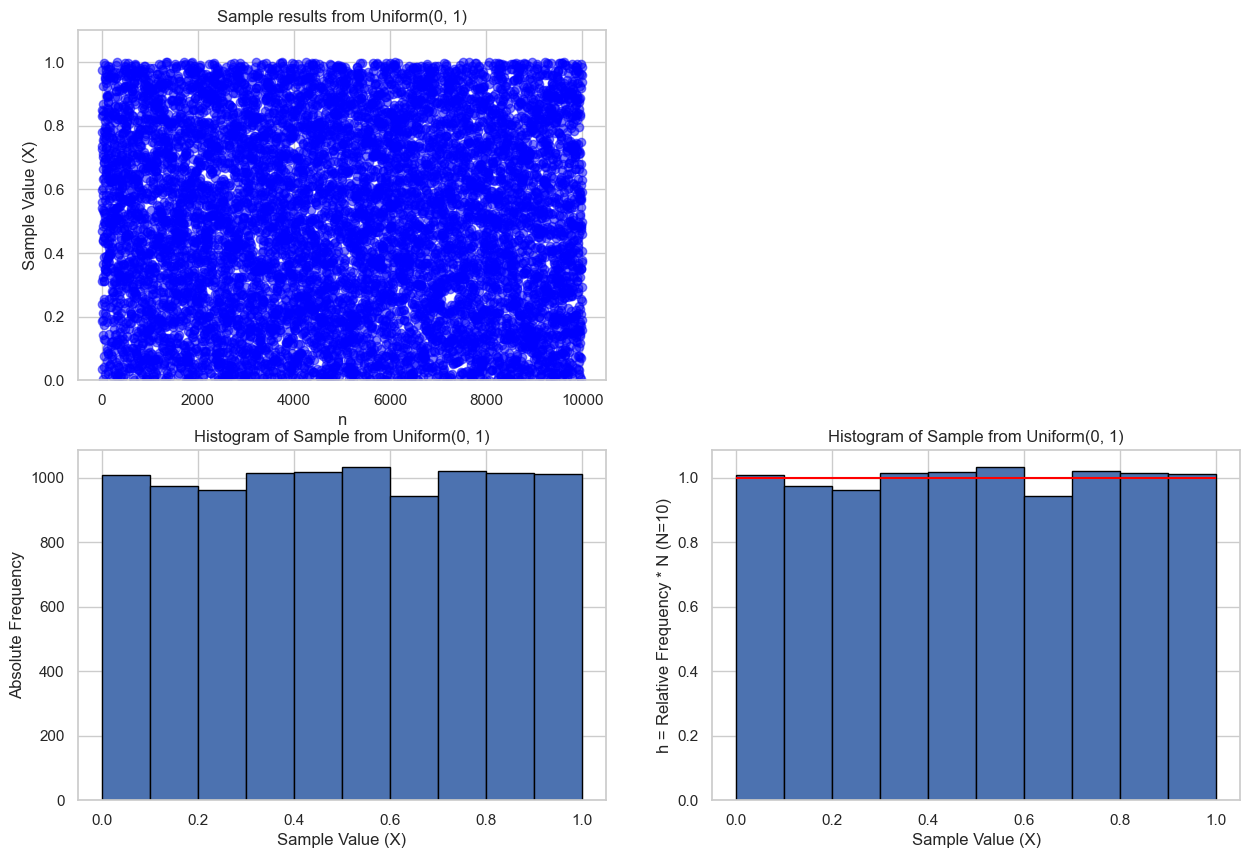
验证采样效果
原理:我们可以通过计算采样结果的直方图,来验证采样数据是否与模型一致。
我们采样 10,000 个 $X \sim \text{Uniform}(2, 5)$,画出直方图看看分布是否均匀:
✅ 如果看到直方图非常接近平的,说明分布是均匀的。
import matplotlib.pyplot as plt
a, b, n = 0, 1, 10000
pdf = 1 / (b - a) # 均匀分布的概率密度函数
samples = sample_uniform_list(a, b, n)
plt.figure(figsize=(15, 10))
# 采样结果
plt.subplot(2, 2, 1)
plt.scatter(range(n), samples, alpha=0.5, color='blue')
plt.title(f"Sample results from Uniform({a}, {b})")
plt.xlabel("n")
plt.ylabel("Sample Value (X)")
plt.ylim(0, 1.1)
# 采样直方图(频率)
N = 10
plt.subplot(2, 2, 3)
plt.hist(samples, bins=N, density=False, edgecolor='black')
plt.title(f"Histogram of Sample from Uniform({a}, {b})")
plt.xlabel("Sample Value (X)")
plt.ylabel("Absolute Frequency")
# 采样直方图(相对频率)
plt.subplot(2, 2, 4)
plt.hist(samples, bins=N, density=True, edgecolor='black')
plt.hlines(pdf, a, b, colors='red', linestyles='solid', label='PDF')
plt.title(f"Histogram of Sample from Uniform({a}, {b})")
plt.xlabel("Sample Value (X)")
plt.ylabel(f"h = Relative Frequency * N (N={N})")
plt.show()
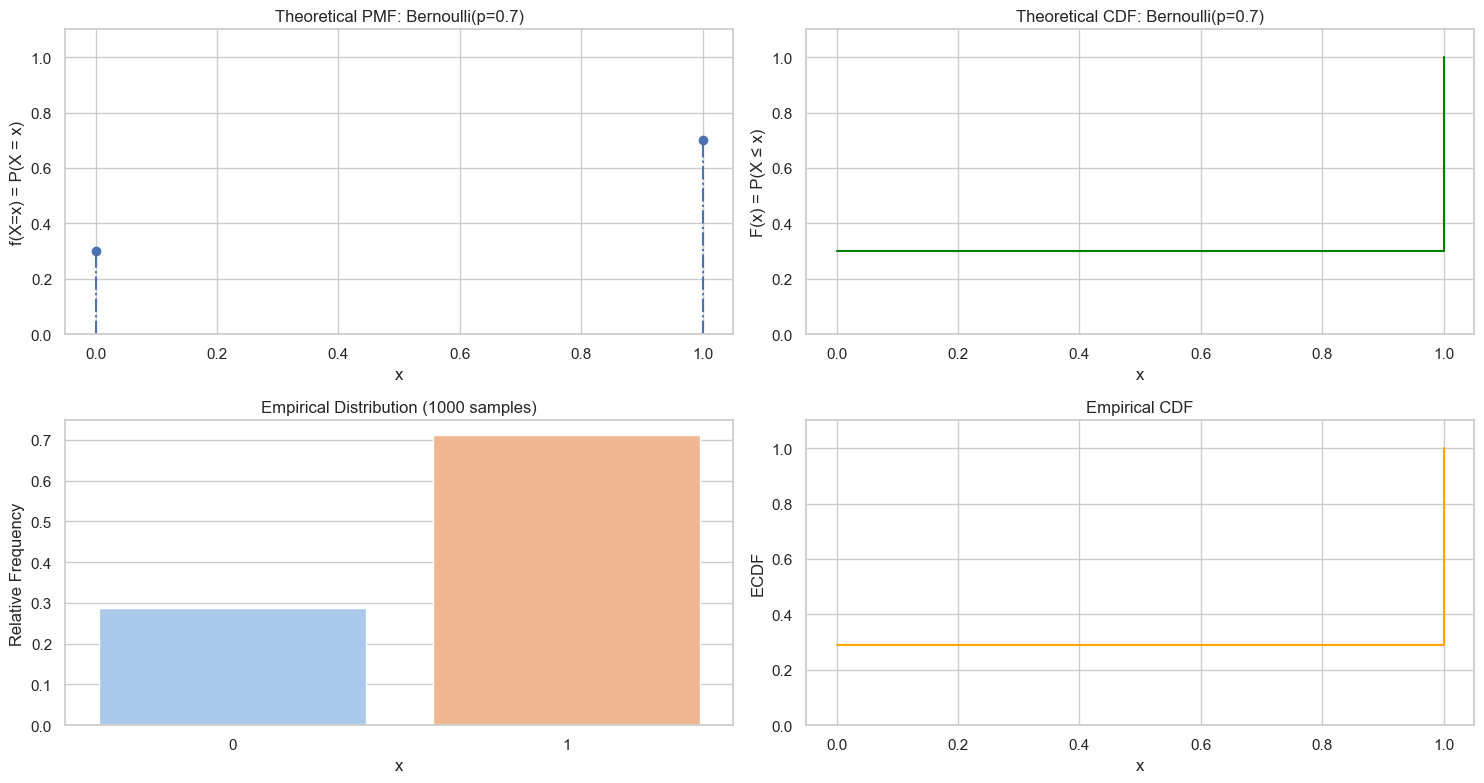
伯努利随机变量(Bernouli RV)
又称两点分布或者0-1分布。离散型随机变量。
数学定义
设 $X \sim \text{Bernouli}(p)$,其中 $0 \le p \le 1$。
支持集(取值范围,值域)是:
$$ k \in \{0, 1\} $$每个值的概率是:
$$ P(X = 1) = p \\ P(X = 0) = 1 - p $$概率质量函数(PMF):
$$ f(X=k) = P(X=k) = \left\{ \begin{aligned} p, \text{if } k=1\\ 1-p, \text{if } k=0 \end{aligned} \right. $$累积分布函数(CDF):
$$ F(X=k) = P(X\le k) = \left\{ \begin{aligned} 0, \text{if } k \lt 0 \\ 1-p, \text{if } 0 \le k \lt 1\\ 1, \text{ for } k \ge 1 \end{aligned} \right. $$期望($\mu$):$p$
方差($\sigma^2$):$p(1-p)$
参考:
import numpy as np
# 设置随机种子以保证结果可重复
np.random.seed(42)
# 1. 定义参数
p = 0.7
values = np.array([0, 1]) # 离散取值:1~6
n = len(values)
pmf = np.array([1-p, p])
cdf = np.cumsum(pmf) # 累积分布函数
# 2. 抽样
n_samples = 1000
samples = np.array([np.random.binomial(n=1, p=p) for _ in range(n_samples)])
# 3. 可视化:理论分布 + 采样频率对比
plot_discrete_rv(values, pmf, cdf, samples, f"Bernoulli(p={p})")
伯努利定理(Bernouli Theorm)
伯努利定理: 描述了概率与频率之间的关系,当重复次数增加时,事件的相对频率会趋近于其概率。
设 $X_1, X_2, ..., X_n$ 是 $n$ 次独立同分布的伯努利随机变量(即 $X_i \sim \text{Bernoulli}(p)$),令
$$ \bar{X}_n = \frac{1}{n} \sum_{i=1}^n X_i $$即成功的相对频率。
那么,伯努利定理告诉我们:
$$ \lim_{n \to \infty} \mathbb{P}\left( \left| \bar{X}_n - p \right| > \epsilon \right) = 0 \quad \text{对任意 } \epsilon > 0 $$因此,我们可以利用伯努利定理来验证模拟采样的正确性:
- 计算每个事件的的实际频率 $f_{a_i}$
- 计算每个事件的相对频率 $f_i = \frac{f_{a_i}}{N}$
- 将每个事件的相对频率 $f_i$ 与概率 $p$ 进行对比。根据伯努利定理,当 $N$ 变大时,$f_i$ 会逼近 $p$
参考:
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
from IPython.display import HTML
# -----------------------------
# 参数设置
# -----------------------------
p = 0.3 # 成功概率
n_trials = 10000 # 总实验次数
interval = 50 # 动画间隔时间(ms)
# -----------------------------
# 生成伯努利实验数据
# -----------------------------
np.random.seed(0)
samples = np.random.binomial(n=1, p=p, size=n_trials)
cumulative_freq = np.cumsum(samples) / np.arange(1, n_trials + 1)
# -----------------------------
# 创建图形
# -----------------------------
fig, ax = plt.subplots(figsize=(8, 4))
ax.set_ylim(0, 1)
ax.set_xlim(1, n_trials)
ax.axhline(y=p, color='red', linestyle='--', label=f'True Probability p = {p}')
line, = ax.plot([], [], lw=2, label='Empirical Frequency')
text = ax.text(0.05, 0.9, '', transform=ax.transAxes)
ax.set_xlabel('Number of Trials')
ax.set_ylabel('Success Frequency')
ax.set_title('Bernoulli Theorem Animation')
ax.legend()
# -----------------------------
# 动画更新函数
# -----------------------------
def update(frame):
x = np.arange(1, frame + 1)
y = cumulative_freq[:frame]
line.set_data(x, y)
text.set_text(f'n = {frame}, freq = {y[-1]:.3f}')
return line, text
# -----------------------------
# 创建动画
# -----------------------------
ani = FuncAnimation(fig, update, frames=np.arange(1, n_trials + 1, 10),
interval=interval, blit=True)
# Save as GIF
from matplotlib.animation import PillowWriter
ani.save("bernoulli_theorem_animation.gif", writer=PillowWriter(fps=10))
plt.close(fig)
from IPython.display import Image
Image(filename="bernoulli_theorem_animation.gif")
#plt.close()
# 在 notebook 中显示动画
#HTML(ani.to_jshtml())
采样
基于均匀分布 Uniform(0, 1)
🌱 原理
利用一个均匀分布 $U \sim \text{Uniform}(0,1)$ 来实现:
- 如果 $U < p$,输出 1(成功)
- 否则输出 0(失败)
这是因为 Uniform(0,1) 在区间内是均匀的,所以概率小于 $p$ 的那一段恰好就是 “成功”的概率。
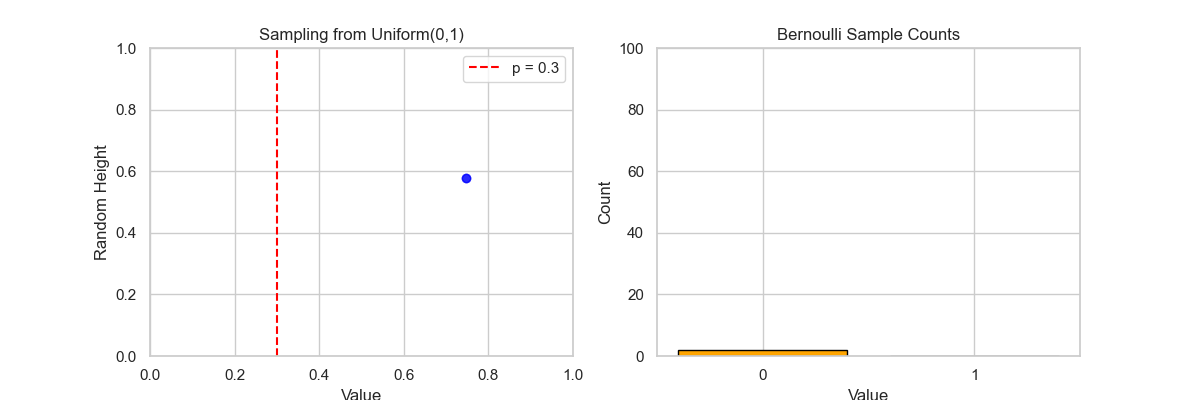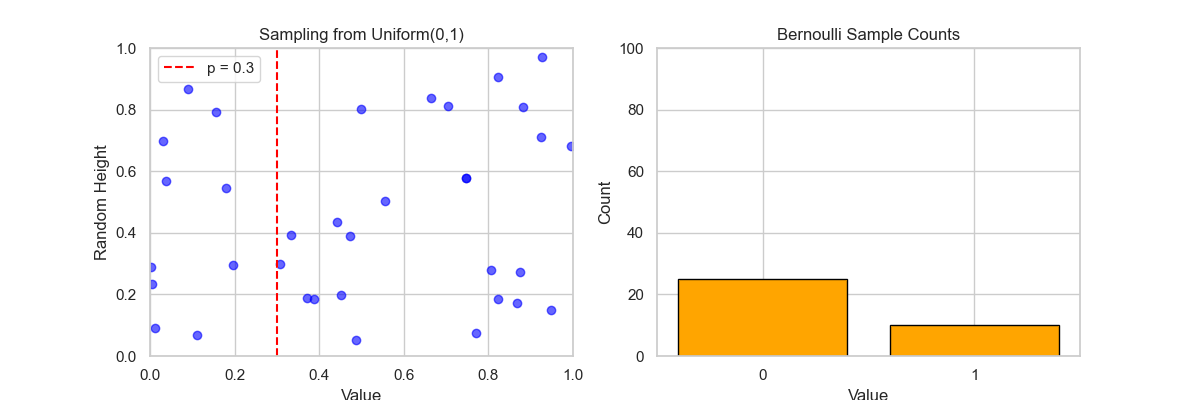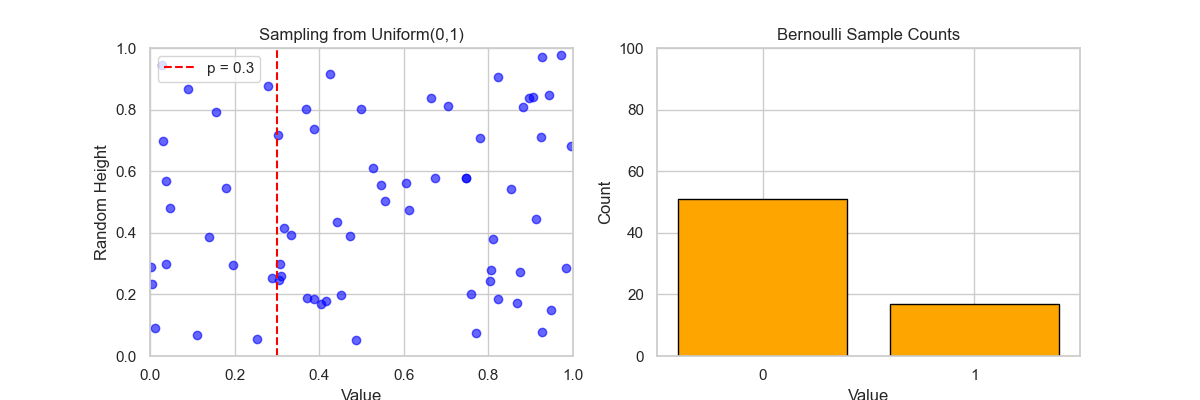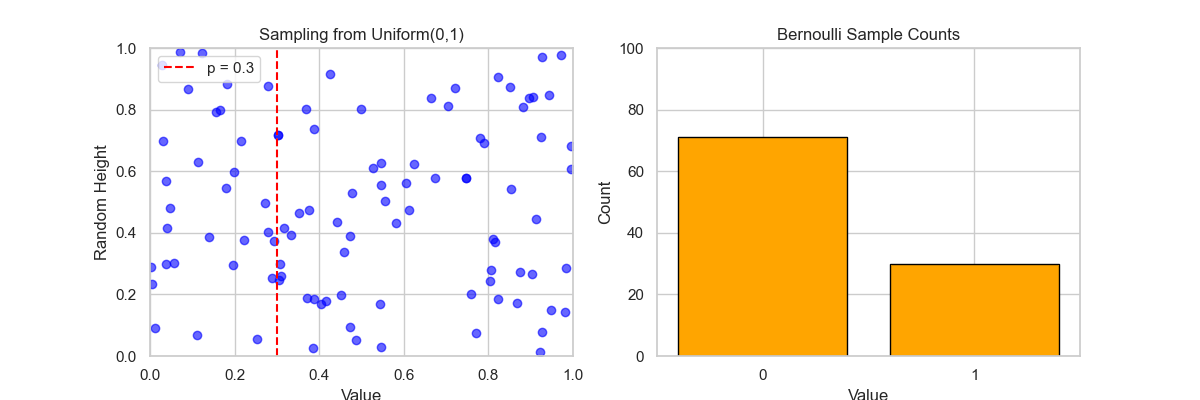
🎬 动画说明: 左图:Sampling from Uniform(0,1)
- 每一帧,生成一个 $U∼Uniform(0,1)$ 的样本;
- 蓝色点按随机高度显示采样值;
- 红色虚线表示阈值 $p=0.3$,即:
- $U
- $U≥p$ ⇒ 伯努利值为 0。
- $U
右图:Bernoulli Sample Counts
- 实时更新 0 和 1 的出现次数柱状图;
- 最终,1 的数量约为 30%,符合概率 $p=0.3$;
- 0 的数量约为 70%。
import matplotlib.pyplot as plt
import matplotlib.animation as animation
import numpy as np
from IPython.display import HTML
# Parameters
p = 0.3
n_frames = 100
# Pre-generate uniform samples
uniform_samples = np.random.uniform(0, 1, n_frames)
bernoulli_samples = (uniform_samples < p).astype(int)
# Set up the figure and axes
fig, axs = plt.subplots(1, 2, figsize=(12, 4))
uniform_ax = axs[0]
bernoulli_ax = axs[1]
# Initialize plots
uniform_scatter = uniform_ax.scatter([], [], c='blue', alpha=0.6)
bernoulli_bar = bernoulli_ax.bar([0, 1], [0, 0], color='orange', edgecolor='black')
# Configure uniform axis
uniform_ax.axvline(p, color='red', linestyle='--', label=f'p = {p}')
uniform_ax.set_xlim(0, 1)
uniform_ax.set_ylim(0, 1)
uniform_ax.set_title('Sampling from Uniform(0,1)')
uniform_ax.set_xlabel('Value')
uniform_ax.set_ylabel('Random Height')
uniform_ax.legend()
uniform_ax.grid(True)
# Configure Bernoulli axis
bernoulli_ax.set_xlim(-0.5, 1.5)
bernoulli_ax.set_ylim(0, n_frames)
bernoulli_ax.set_title('Bernoulli Sample Counts')
bernoulli_ax.set_xlabel('Value')
bernoulli_ax.set_ylabel('Count')
bernoulli_ax.set_xticks([0, 1])
bernoulli_ax.grid(True)
# Store sample counts
count_0 = 0
count_1 = 0
x_vals = []
y_vals = []
# Animation update function
def update(frame):
global count_0, count_1, x_vals, y_vals
u = uniform_samples[frame]
x_vals.append(u)
y_vals.append(np.random.rand()) # random y position for scatter
bern_sample = bernoulli_samples[frame]
if bern_sample == 0:
count_0 += 1
else:
count_1 += 1
# Update scatter
uniform_scatter.set_offsets(np.column_stack((x_vals, y_vals)))
# Update bar chart
bernoulli_bar[0].set_height(count_0)
bernoulli_bar[1].set_height(count_1)
return uniform_scatter, bernoulli_bar
# Create animation
ani = animation.FuncAnimation(fig, update, frames=n_frames, interval=100, blit=False)
# 保存为 GIF
from matplotlib.animation import PillowWriter
ani.save("sample_uniform_to_bernoulli.gif", writer=PillowWriter(fps=10))
plt.close(fig)
from IPython.display import Image
Image(filename="sample_uniform_to_bernoulli.gif")
#plt.close()
# 在 notebook 中显示动画
#HTML(ani.to_jshtml())
import random
def sample_bernoulli(p):
U = random.random() # U ~ Uniform(0, 1)
return 1 if U < p else 0
sample_bernoulli(0.7)
1
验证
p, N = 0.7, 10000
samples = [sample_bernoulli(p) for _ in range(N)]
print(f"Empirical mean: {sum(samples)/len(samples):.3f}") # 应该接近 0.7
Empirical mean: 0.703
使用 numpy
import numpy as np
np.random.binomial(n=1, p=0.7)
1
验证
p, N = 0.7, 10000
samples = [np.random.binomial(n=1, p=p) for _ in range(N)]
print(f"Empirical mean: {sum(samples)/len(samples):.3f}") # 应该接近 0.7
Empirical mean: 0.702
二项随机变量(Binomial Random Variable)
一个随机变量 $X∼Binomial(n,p)$,表示在重复进行 $n$ 次独立的伯努利试验(每次成功概率为 $p$)中,成功(记为1)发生的总次数。$X$ 是离散随机变量。
数学定义
设 $X \sim \text{Binomial}(n, p)$(或者是 $X \sim B(n,p)$),其中 $n \gt 0, 0 \le p \le 1$。
支持集(取值范围,值域)是:
$$ k \in \{0, \dots, n\} $$- 表示成功的次数
每个值的概率是:
$$ P(X = 0) = (1-p)^n\\ \dots \\ P(X = k) = \begin{pmatrix} n \\ k \end{pmatrix}p^k(1-p)^{(n-k)} \\ \dots \\ P(X = n) = p^n $$
概率质量函数(PMF):
$$ f(X=k) = P(X=k) = \begin{pmatrix} n \\ k \end{pmatrix}p^k(1-p)^{(n-k)} \\ 其中,\begin{pmatrix} n \\ k \end{pmatrix} = \frac{n!}{k!(n-k)!} $$累积分布函数(CDF):
$$ F(X=k) = P(X\le k) = \sum _{i=0}^{\lfloor k\rfloor }{n \choose i}p^{i}(1-p)^{n-i} $$- where $\lfloor k\rfloor$ is the “floor” under k, i.e. the greatest integer less than or equal to k.
期望($\mu$):$np$
- If $X_{1},\ldots ,X_{n}$ are identical (and independent) Bernoulli random variables with parameter $p$, then $X = X_1 + \dots + X_n$ and $\operatorname {E} [X]=\operatorname {E} [X_{1}+\cdots +X_{n}]=\operatorname {E} [X_{1}]+\cdots +\operatorname {E} [X_{n}]=p+\cdots +p=np.$
方差($\sigma^2$):$np(1-p)$
- the variance of a sum of independent random variables = the sum of the variances
参考:
from scipy.stats import binom
import numpy as np
# 设置随机种子以保证结果可重复
np.random.seed(42)
# 1. 定义参数
n, p = 5, 0.3 # X ~ Binomial(n, p)
values = range(n + 1) # 离散取值:0, 1, ..., n
pmf = binom.pmf(values, n, p)
cdf = np.cumsum(pmf) # 累积分布函数
# 2. 抽样
n_samples = 1000
samples = np.random.binomial(n=n, p=p, size=n_samples)
# 3. 可视化:理论分布 + 采样频率对比
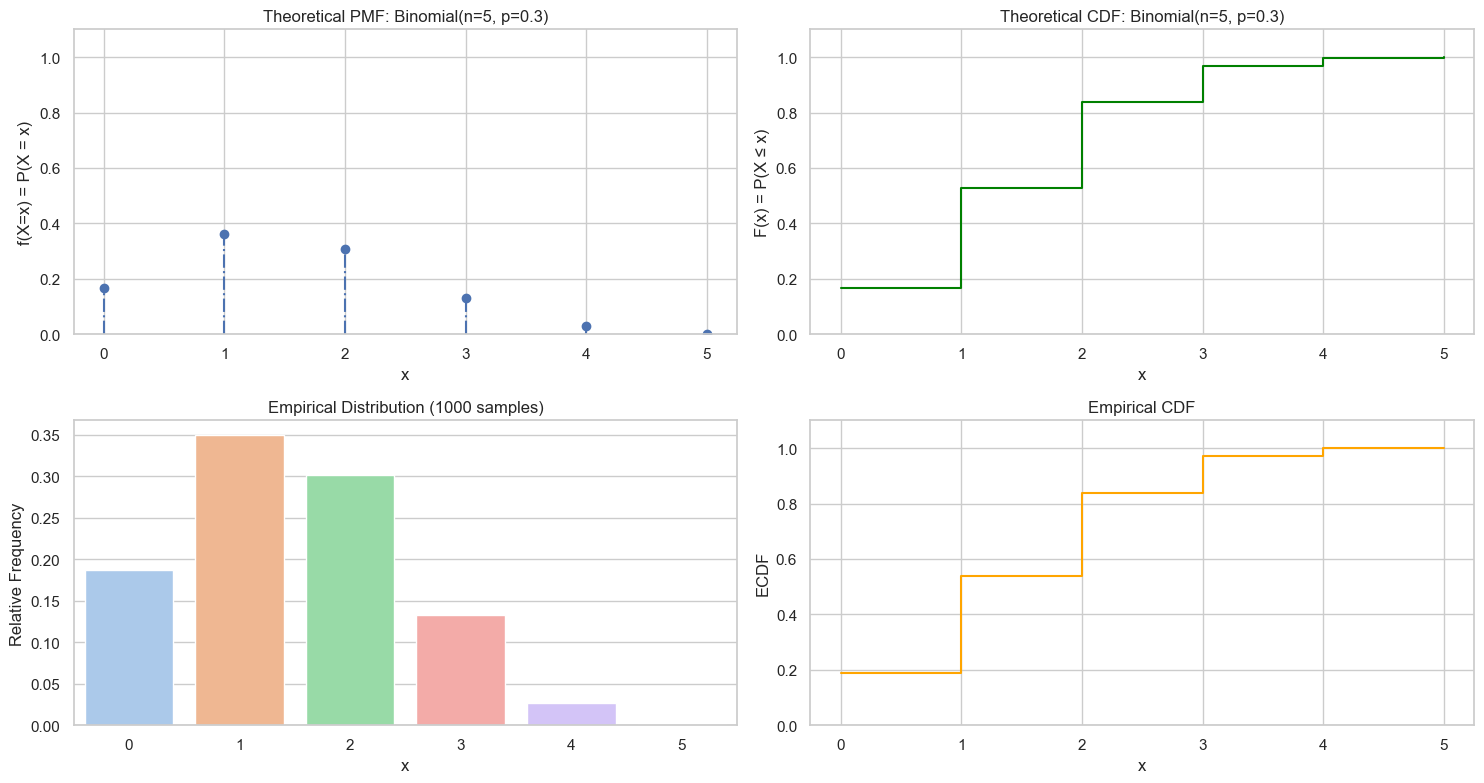
plot_discrete_rv(values, pmf, cdf, samples, f'Binomial(n={n}, p={p})')
采样
采样 Binomial 随机变量 $X \sim \text{Binomial}(n, p)$(表示从 $n$ 次独立伯努利试验中成功次数)的方法很多,适用于不同参数范围。下面是目前已知的所有经典和实用方法,按类型归类整理,并指出适用情况。
| 方法 | 主要思想 | 适用范围 | 是否精确 | 是否容易实现 |
|---|---|---|---|---|
| 1. Bernoulli 重复法 | 对 $n$ 次伯努利采样并求和 | 任意 $n, p$,尤其是小 $n$ | ✅ 精确 | ✅ 简单 |
| 2. 反函数采样法(Inverse Transform) | 用 CDF 找第一个使 $F(k) ≥ u$ 的 $k$ | 小 $n$ 时可行 | ✅ 精确 | ⚠️ 易慢 |
| 3. 表查找法(CDF 查表) | 预计算所有 $F(k)$,再查 | 小 $n$(<100) | ✅ 精确 | ✅ 快速(预计算) |
| 4. Rejection Sampling | 构造易采样的 proposal 分布再拒绝 | 中等 $n$,或用于模拟 | ✅ 精确 | ⚠️ 难度高 |
| 5. 正态近似法(Normal Approximation) | 用 $\mathcal{N}(np, np(1-p))$ 近似 | 大 $n$,$np(1-p) \ge 10$ | ❌ 近似 | ✅ 非常快 |
| 6. Poisson 近似法 | 当 $n$ 大、$p$ 小,$\lambda = np$ | $p \le 0.05$,$np \le 10$ | ❌ 近似 | ✅ 快速 |
| 7. BTPE 算法(Fast Binomial by Kachitvichyanukul and Schmeiser) | 分段拒绝采样(经典高效) | 任意 $n, p$,特别适合大 $n$ | ✅ 精确 | ⚠️ 实现复杂 |
| 8. 比特操作法(Bit Trick) | 用位操作模拟多次伯努利 | $n$ 不大(如蒙特卡洛) | ✅ 精确 | ⚠️ 特殊优化 |
| 9. Alias 方法(非主流) | 离散变量的高效采样 | 很小 $n$ 且大量重复采样 | ✅ 精确 | ⚠️ 初始化复杂 |
🔧 推荐使用
| 使用场景 | 推荐方法 |
|---|---|
| 学习理解原理 | 伯努利重复采样 / 反函数采样 |
| 小样本、单次采样 | 任意(都快) |
| 大样本、速度优先 | 正态近似或 BTPE(使用 numpy.random.binomial) |
| 小 $p$、稀疏事件 | Poisson 近似 |
| 多次重复采样 | 使用查表 / BTPE 算法 |
✅ 总结图示(概念流程)
Binomial(n, p)
│
├── 小 n: 直接伯努利重复
├── 小 p: 用 Poisson(np)
├── 大 n, np(1-p)>10: 用正态(np, np(1-p))
├── 任意 n,p: 反函数 or 查表
└── 高效工业级: BTPE 算法(NumPy)
import matplotlib.pyplot as plt
from math import comb
def verify_binomial_sample(n, p, samples):
"""
验证二项分布采样的正确性
:param n: 二项分布的试验次数
:param p: 成功概率
:param samples: 采样结果列表
:return: None
"""
N = len(samples)
empirical_mean = sum(samples) / N
theoretical_mean = n * p
print(f"Empirical mean: {empirical_mean:.3f}, Theoretical mean: {theoretical_mean:.3f}")
empirical_variance = sum((x - empirical_mean) ** 2 for x in samples) / len(samples)
theoretical_variance = n * p * (1 - p)
print(f"Empirical variance: {empirical_variance:.3f}, Theoretical variance: {theoretical_variance:.3f}")
# 统计频率
counts = [samples.count(k) / N for k in range(n + 1)]
# 计算理论概率(PMF)
theoretical = [comb(n, k) * (p ** k) * ((1 - p) ** (n - k)) for k in range(n + 1)]
# 可视化
plt.figure(figsize=(10, 6))
plt.bar(range(n + 1), counts, width=0.4, label='Sampled Frequency', color='skyblue', align='edge')
plt.bar([k - 0.4 for k in range(n + 1)], theoretical, width=0.4, label='Theoretical PMF', color='orange', align='edge')
plt.xlabel("Number of Successes")
plt.ylabel("Probability")
plt.title(f"Binomial Distribution: n={n}, p={p}")
plt.legend()
plt.grid(True)
plt.show()
方法一:伯努利重复法(基于伯努利随机变量)
如果你能从伯努利分布中采样,那就可以通过对 $n$ 次伯努利采样求和,得到一个二项式样本。
✅ 步骤概览:
- 初始化计数器为 0
- 重复 n 次以下操作:
- 从 [0, 1] 中采样一个伯努利值(成功的概率是 $p$)
- 如果采样为 1(表示成功),则计数器加一
- 最终的计数器数值就是一次二项分布的采样值
使用 NumPy 向量化采样:
import numpy as np
np.random.binomial(n=10, p=0.5, size=1000)
import random
def sample_binomial_mimic(n, p):
count = 0
for _ in range(n): # repeat N times Bernouli sampling
u = random.random() # 从 [0,1) 中采样一个均匀变量
if 1-p <= u < 1:
count += 1 # 成功就加一
return count
def sample_binomial_mimic_list(n, p, num_samples):
return [sample_binomial_mimic(n, p) for _ in range(num_samples)]
n, p, num_samples = 10, 0.5, 10
sample_binomial_mimic_list(n, p, num_samples)
[2, 5, 6, 4, 4, 4, 7, 4, 8, 5]
Visualize
import matplotlib.pyplot as plt
n, p, num_samples = 10, 0.3, 1000
samples = sample_binomial_mimic_list(n, p, num_samples)
plt.hist(samples, bins=range(12), align='left', rwidth=0.8, color='skyblue')
plt.xlabel("Number of Successes")
plt.ylabel("Frequency")
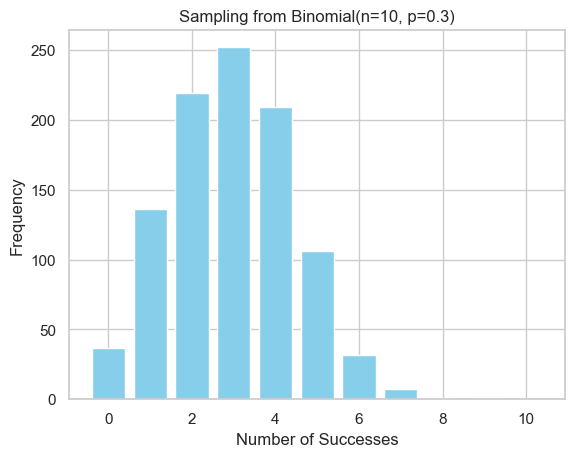
plt.title("Sampling from Binomial(n=10, p=0.3)")
plt.show()
验证
验证的思路是:采很多样本,然后画出直方图,再与理论的二项式概率质量函数(PMF)对比。
# 采样
n = 10
p = 0.3
N = 10000 # 采样次数
samples = sample_binomial_mimic_list(n, p, N)
#print(f"Empirical mean: {sum(samples)/len(samples):.3f}") # 应该接近 np = 10x0.4 = 4.0
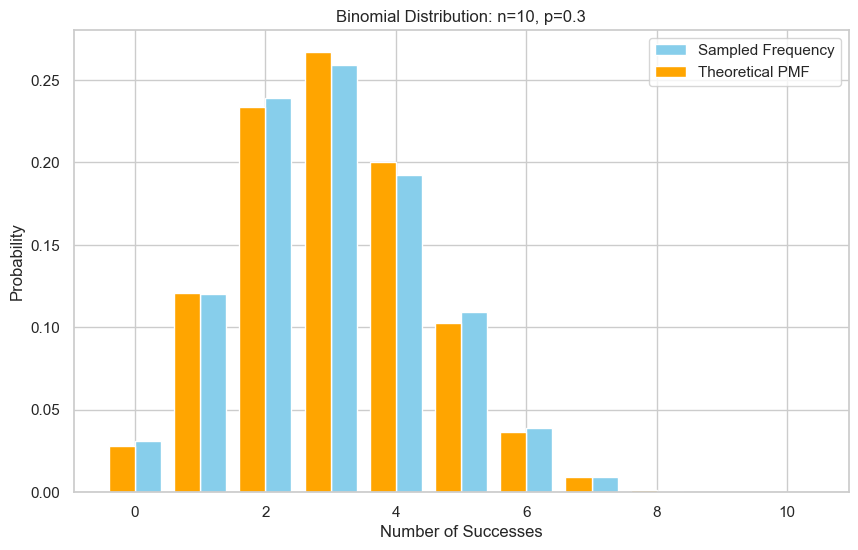
verify_binomial_sample(n, p, samples)
Empirical mean: 2.997, Theoretical mean: 3.000
Empirical variance: 2.153, Theoretical variance: 2.100
方法二:反函数采样法(Inverse Transform)
它是一种非常经典的、不依赖于重复模拟伯努利分布的采样方法。不过它不太适合高 n 的 Binomial,因为它涉及累积概率的查找和搜索,但在理论上,它是完全可行的,而且 没有用到伯努利随机变量!
原理步骤如下:
生成一个均匀随机数 $u \sim \text{Uniform}(0, 1)$
依次累加二项式分布的概率质量函数(PMF):
$$ F(k) = \sum_{i=0}^{k} P(X=i) $$找到第一个 $k$,使得 $F(k) \ge u$
返回这个 $k$,作为采样结果
这就完成了一次采样。
优缺点分析
| 优点 | 缺点 |
|---|---|
| 理论通用性强 | 对高维、高 n 的二项分布效率较低(要计算很多项) |
| 不需要模拟伯努利 | 每次采样都要重新从 k=0 开始扫描 |
| 可用于精确的采样 | 无法向量化,不能直接并行加速 |
适合用在:
- $n$ 较小的情况(如 $n \leq 20$)
- 教学和理论验证目的
📌 总结
| 方法 | 是否用伯努利 | 速度 | 适用情况 |
|---|---|---|---|
| 累加伯努利 | ✅ | 快(简单) | 通用、小 n |
| 逆变换采样 | ❌ | 中等 | 理论验证、非向量化场景 |
| 正态/泊松近似 | ❌ | 快 | n 大、p 小/中 |
| 表查法 + 二分查找 | ❌ | 非常快 | 固定 n,多次采样 |
辅助示意图理解
如果你画出 Binomial(n=5, p=0.5) 的 PMF:
| k | P(X=k) | 累积和 F(k) |
|---|---|---|
| 0 | 0.03125 | 0.03125 |
| 1 | 0.15625 | 0.1875 |
| 2 | 0.3125 | 0.5 |
| 3 | 0.3125 | 0.8125 |
| 4 | 0.15625 | 0.96875 |
| 5 | 0.03125 | 1.0 |
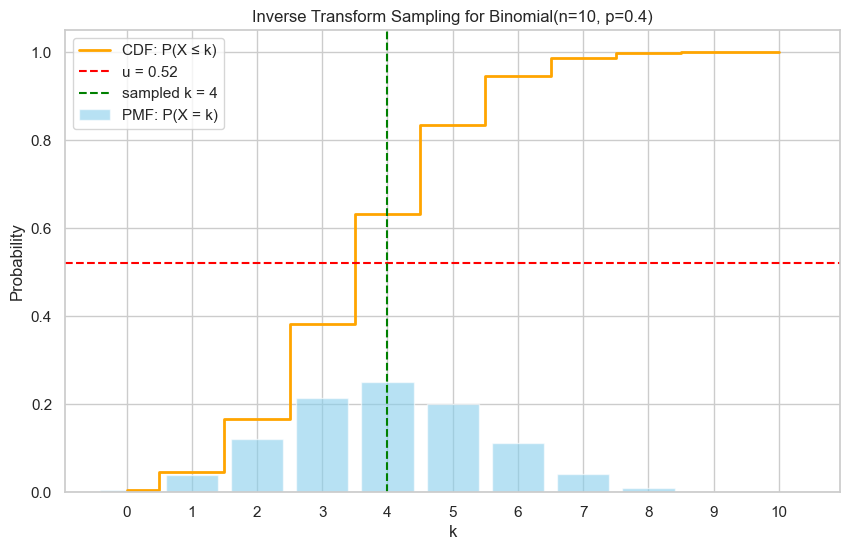
如果你生成一个 $u = 0.4$,你会发现 $F(2) = 0.5 \ge 0.4$,那么就采样出 $k = 2$。
import matplotlib.pyplot as plt
from math import comb
import numpy as np
import random
# 参数
n = 10
p = 0.4
# 计算 PMF 和 CDF
k_vals = list(range(n + 1))
pmf = [comb(n, k) * p**k * (1 - p)**(n - k) for k in k_vals]
cdf = np.cumsum(pmf)
####### 采样 #######
# 生成一个随机数 u
u = 0.52 # 也可以改成 random.random()
# 找到第一个 cdf[k] >= u
k_selected = None
for k, value in enumerate(cdf):
if u <= value:
k_selected = k
break
####### 绘制验证 #######
# 绘图
plt.figure(figsize=(10, 6))
# PMF 图(柱状图)
plt.bar(k_vals, pmf, alpha=0.6, label='PMF: P(X = k)', color='skyblue')
# CDF 图(阶梯线)
plt.step(k_vals, cdf, where='mid', color='orange', label='CDF: P(X ≤ k)', linewidth=2)
# 画出 u 和对应的 k_selected
plt.axhline(y=u, color='red', linestyle='--', label=f'u = {u:.2f}')
plt.axvline(x=k_selected, color='green', linestyle='--', label=f'sampled k = {k_selected}')
# 标注
plt.title(f"Inverse Transform Sampling for Binomial(n={n}, p={p})")
plt.xlabel("k")
plt.ylabel("Probability")
plt.legend()
plt.grid(True)
plt.xticks(k_vals)
plt.ylim(0, 1.05)
plt.show()
代码实现
import random
from math import comb
def sample_binomial_inverse(n, p):
# Step 1: generate a uniform random number
u = random.random()
# Step 2: initialize cumulative probability
cumulative = 0.0
for k in range(n + 1):
prob = comb(n, k) * (p ** k) * ((1 - p) ** (n - k))
cumulative += prob
if u <= cumulative:
return k
return n # fallback
def sample_binomial_inverse_list(n, p, num_samples):
return [sample_binomial_inverse(n, p) for _ in range(num_samples)]
n, p, num_samples = 10, 0.5, 10
sample_binomial_inverse_list(n, p, num_samples)
[3, 4, 2, 3, 5, 5, 7, 2, 4, 8]
可视化
import matplotlib.pyplot as plt
n, p, num_samples = 10, 0.3, 1000
samples = sample_binomial_inverse_list(n, p, num_samples)
plt.hist(samples, bins=range(12), align='left', rwidth=0.8, color='skyblue')
plt.xlabel("Number of Successes")
plt.ylabel("Frequency")
plt.title("Sampling from Binomial(n=10, p=0.3)")
plt.show()
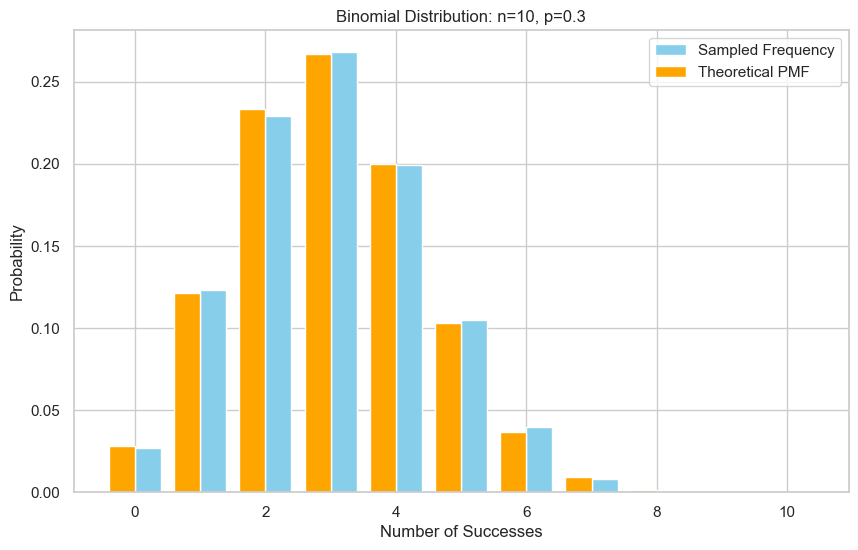
验证
# 采样
n = 10
p = 0.3
N = 10000 # 采样次数
samples = sample_binomial_inverse_list(n, p, N)
#print(f"Empirical mean: {sum(samples)/len(samples):.3f}") # 应该接近 np = 10x0.4 = 4.0
verify_binomial_sample(n, p, samples)
Empirical mean: 3.011, Theoretical mean: 3.000
Empirical variance: 2.097, Theoretical variance: 2.100
方法三:表查找法(CDF 查表)
import random
from math import comb
binomial_table, binomial_table_n, binomial_table_p = None, None, None
def generate_binomial_table(n, p):
"""
生成二项分布的 CDF 查找表
:param n: 二项分布的试验次数
:param p: 成功概率
:return: None
"""
global binomial_table
binomial_table = {}
cumulative = 0.0
for k in range(n + 1):
prob = comb(n, k) * (p ** k) * ((1 - p) ** (n - k))
cumulative += prob
binomial_table[k] = cumulative
def sample_binomial_table(n, p):
# Step 1: generate a uniform random number
u = random.random()
# Step 2: look up in the CDF table
if binomial_table is None or binomial_table_n != n or binomial_table_p != p:
generate_binomial_table(n, p)
# Step 3: find the first k such that CDF[k] >= u
for k in range(n + 1):
if u <= binomial_table[k]:
return k
# If no k found, return n
return n # fallback
def sample_binomial_table_list(n, p, num_samples):
return [sample_binomial_table(n, p) for _ in range(num_samples)]
验证
# 采样
n = 10
p = 0.3
N = 10000 # 采样次数
samples = sample_binomial_table_list(n, p, N)
#print(f"Empirical mean: {sum(samples)/len(samples):.3f}") # 应该接近 np = 10x0.4 = 4.0
verify_binomial_sample(n, p, samples)
Empirical mean: 3.002, Theoretical mean: 3.000
Empirical variance: 2.100, Theoretical variance: 2.100
方法四:拒绝-采样法(Rejection Sampling)
使用 Rejection Sampling(接受-拒绝采样)来采样一个二项式随机变量,其实并不是最常见的方法(更常用的是直接采样或用泊松/正态近似),但它在理论上是可行的,尤其在难以直接采样或需要从截断/罕见参数的二项式分布中采样时。
✅ proposal 分布的理想选择:均匀分布 $g(k) = \frac{1}{n+1}$
- 简单易实现;
- 但若目标分布是偏斜的(如 $p=0.05$),那么大多数 sample 会被拒绝(效率差);
- 仍然是教学中最常用示例。
⚠️ 注意事项:
- 效率取决于 M:如果 $p$ 很小或很大,$f(k)$ 会非常偏,导致很低的接受率;
- 若想更高效,可使用离散高斯分布、泊松分布、正态近似等作为更“贴近”目标的 proposal 分布;
- Rejection Sampling 的通用性强,但不是采样 Binomial 的首选方法(首选是直接算法、或正态/泊松近似)。
✅ 总结
| 步骤 | 内容 |
|---|---|
| 🎯 目标 | 从 Binomial(n, p) 中采样 |
| 🧰 方法 | 构造 proposal $g(k)$,满足 $f(k) \leq M g(k)$ |
| 📐 采样机制 | 采样 $k \sim g(k)$,以概率 $\alpha = \frac{f(k)}{M g(k)}$ 接受 |
| 📉 缺点 | 效率受 $p$ 和 $M$ 影响较大,采样较慢 |
| 🧠 优势 | 思路简单、分布通用性强 |
import numpy as np
from scipy.stats import binom
import matplotlib.pyplot as plt
def rejection_sample_binomial(n, p, N_samples=1000):
samples = []
# 目标分布:Bin(n, p)
bin_pmf = [binom.pmf(k, n, p) for k in range(n+1)]
# Proposal 分布:Uniform(0, n)
g = 1.0 / (n + 1)
# 找最大值用于计算 M
M = max(bin_pmf) / g
while len(samples) < N_samples:
k = np.random.randint(0, n+1)
u = np.random.uniform(0, 1)
accept_prob = bin_pmf[k] / (M * g)
if u < accept_prob:
samples.append(k)
return samples
# 验证
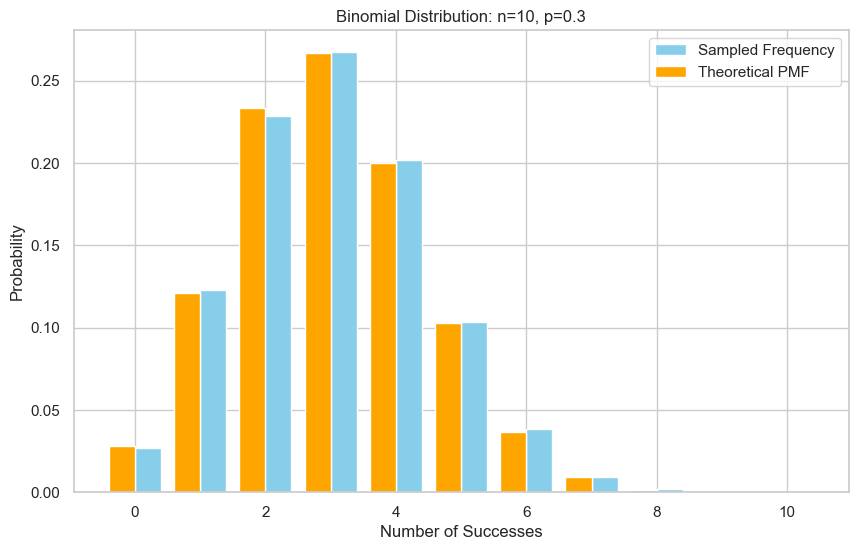
# 采样
n = 10
p = 0.3
N = 10000 # 采样次数
samples = rejection_sample_binomial(n, p, N)
#print(f"Empirical mean: {sum(samples)/len(samples):.3f}") # 应该接近 np = 10x0.4 = 4.0
verify_binomial_sample(n, p, samples)
Empirical mean: 3.014, Theoretical mean: 3.000
Empirical variance: 2.120, Theoretical variance: 2.100
方法五:正态近似法(Normal Approximation)
原理:De Moivre–Laplace 中心极限定理
当 $n$ 足够大时,二项式分布 $X \sim \text{Bin}(n, p)$ 可由正态分布近似:
$$ X \approx Y \sim \mathcal{N}(\mu, \sigma^2) $$其中:
- 均值:$\mu = np$
- 方差:$\sigma^2 = np(1-p)$
这意味着我们可以从该正态分布中采样一个值作为近似。
适用条件:
- $n$ 要足够大
- $p$ 不要太接近 0 或 1
通常经验法则是:
$$ np \geq 10 \quad \text{且} \quad n(1-p) \geq 10 $$采样方法
- 从标准正态分布 $Z \sim \mathcal{N}(0, 1)$ 采样;
- 构造 $Y = np + \sqrt{np(1-p)} \cdot Z$
- 将 $Y$ 四舍五入得到整数 $k$,并裁剪到合法范围 $[0, n]$
误差分析
| 项目 | 描述 |
|---|---|
| 误差来源 | 连续 → 离散、近似 tail 偏差 |
| 效果最好 | $p \approx 0.5$ 且 $n$ 足够大 |
| 偏态情况 | 当 $p \ll 0.5$ 或 $p \gg 0.5$ 时尾部误差大 |
| 改进方法 | 加 continuity correction(见下) |
🔧 Continuity Correction(连续性修正)
由于正态分布是连续的,而二项式是离散的,连续性修正可略微提升精度:
- 将离散值 $k$ 映射到 $[k - 0.5, k + 0.5]$ 的区间上;
- 采样时加 0.5 或 -0.5 抵消误差:
代码中可尝试 samples = np.floor(samples + 0.5).astype(int)。
import numpy as np
from scipy.stats import binom
import matplotlib.pyplot as plt
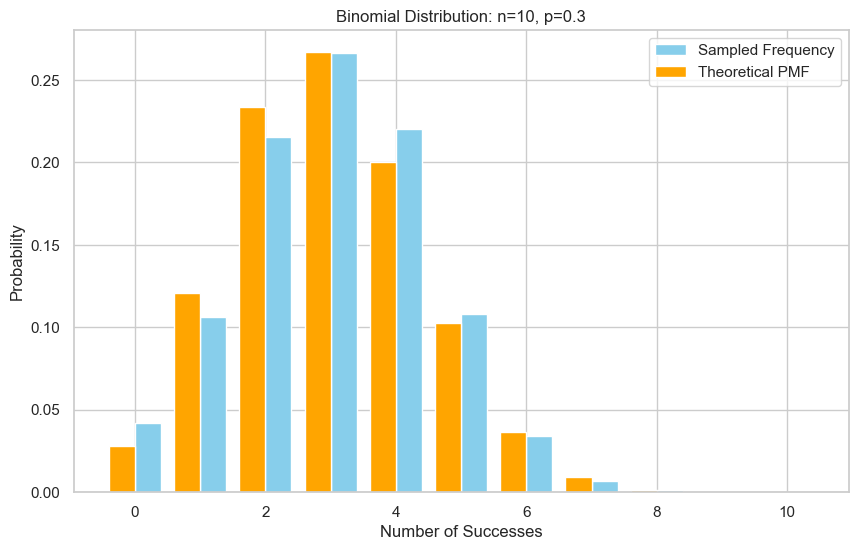
def normal_approx_binomial(n, p, N_samples=10000):
mu = n * p
sigma = np.sqrt(n * p * (1 - p))
# 采样
samples = np.random.normal(loc=mu, scale=sigma, size=N_samples)
# 四舍五入并裁剪
samples = np.round(samples).astype(int)
samples = np.clip(samples, 0, n)
return samples.tolist()
# 验证
# 采样
n = 10
p = 0.3
N = 10000 # 采样次数
samples = normal_approx_binomial(n, p, N)
#print(f"Empirical mean: {sum(samples)/len(samples):.3f}") # 应该接近 np = 10x0.4 = 4.0
verify_binomial_sample(n, p, samples)
Empirical mean: 3.019, Theoretical mean: 3.000
Empirical variance: 2.116, Theoretical variance: 2.100
指数随机变量(Exponential Random Variables)
连续型随机变量。指数分布可以用来建模平均发生率恒定、连续、独立的事件发生的间隔。
数学定义
对于一个参数为 $\lambda > 0$ 的指数分布 $X \sim \text{Exp}(\lambda)$:
支持集(取值范围,值域)是:$X \in [0, \infty]$
概率密度函数(PDF):
$$ f_X(x) = \begin{cases} \lambda e^{-\lambda x}, & x \geq 0 \\ 0, & x < 0 \end{cases} $$累积分布函数(CDF):
$$ F_X(x) = \begin{cases} 1 - e^{-\lambda x}, & x \geq 0 \\ 0, & x < 0 \end{cases} $$期望($\mu$):$\frac{1}{\lambda}$
方差($\sigma^2$):$\frac{1}{\lambda^2}$
参考:
- Wiki: Exponential distribution
- ProofWiki: Expectation of Exponential Distribution
- ProofWiki: Variance of Exponential Distribution
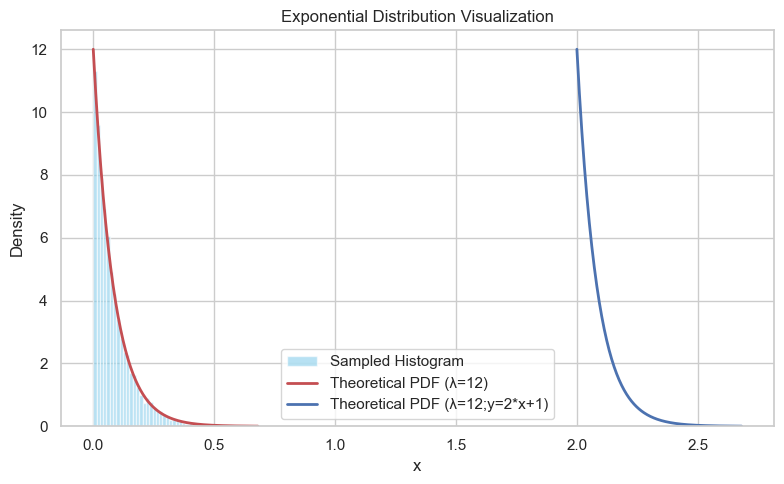
import numpy as np
import matplotlib.pyplot as plt
# 设置随机种子以保证可重复性
np.random.seed(42)
# 指数分布参数 λ(速率参数)
lambda_val = 12
# 采样数量
n_samples = 10000
# 使用 numpy 采样
samples = np.random.exponential(scale=1/lambda_val, size=n_samples)
# 创建图形
plt.figure(figsize=(8, 5))
# 绘制采样的直方图(归一化为密度)
plt.hist(samples, bins=50, density=True, alpha=0.6, color='skyblue', label='Sampled Histogram')
# 生成理论曲线
x_vals = np.linspace(0, np.max(samples), 200)
pdf = lambda_val * np.exp(-lambda_val * x_vals)
plt.plot(x_vals, pdf, 'r-', lw=2, label=f'Theoretical PDF (λ={lambda_val})')
a, b = 2, 1
y_vals = a+b*x_vals
ypdf = a*pdf+b
plt.plot(y_vals, pdf, 'b-', lw=2, label=f'Theoretical PDF (λ={lambda_val};y={a}*x+{b})')
# 图形设置
plt.title('Exponential Distribution Visualization')
plt.xlabel('x')
plt.ylabel('Density')
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()
采样
使用反函数法(Inverse Transform Sampling)
假设我们有一个均匀分布 $U∼Uniform(0,1)$,可以用反函数法来采样指数随机变量:
$ X = -\frac{ln(1-U)}{\lambda}$
推导 $$ F(x) = 1 - e^{-\lambda x} = u\ 1 - u = e^{-\lambda x} \ ln(1-u) = -\lambda x \ x = -\frac{ln(1-u)}{\lambda}
$$
👉 这个公式非常常见,也是在模拟指数分布时的基本方法。
也可以用
numpy.random.exponential(scale=1/lambda_val, size=n_samples)
import random
import math
def sample_exponential_inverse(lambda_val):
"""
采样指数分布
:param lambda_val: 指数分布的速率参数 λ
:param n_samples: 采样数量
:return: 采样结果
"""
u = random.random() # 从 [0, 1) 中采样一个均匀变量
return -math.log(1-u) / lambda_val # 使用逆变换采样公式 X = -ln(1-U)/λ
def sample_exponential_inverse_list(lambda_val, n_samples):
return [sample_exponential_inverse(lambda_val) for _ in range(n_samples)]
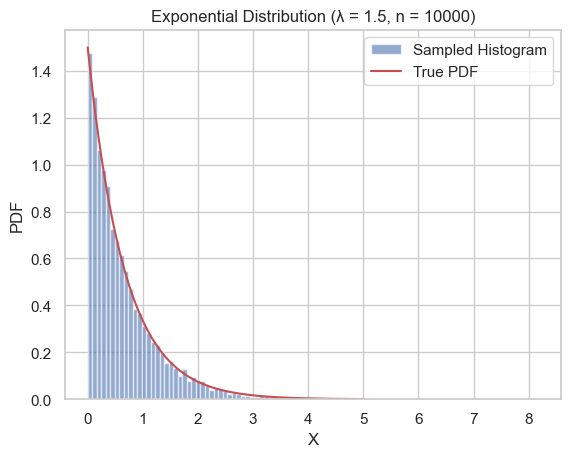
import numpy as np
import matplotlib.pyplot as plt
# 参数设置
lambda_val = 1.5
n = 10000
# 使用反函数法采样
X = sample_exponential_inverse_list(lambda_val, n)
# 验证:绘图
plt.hist(X, bins=100, density=True, alpha=0.6, label='Sampled Histogram')
x_vals = np.linspace(0, 5, 200)
plt.plot(x_vals, lambda_val * np.exp(-lambda_val * x_vals), 'r-', label='True PDF')
plt.xlabel('X')
plt.ylabel('PDF')
plt.title('Exponential Distribution (λ = {:.1f}, n = {})'.format(lambda_val, n))
plt.legend()
plt.show()
几何随机变量(Geometric Random Variables)
概述
它是离散型随机变量中非常经典的一个,出现在很多试验直到第一次成功的情景中。
一个几何随机变量 $X \sim \text{Geometric}(p)$,表示:
在独立重复伯努利试验中,第一次成功出现的试验编号。
- 每次试验都是独立的,成功概率是 $p \in (0,1)$
- $X \in \{1, 2, 3, \dots\}$
📌 概率质量函数(PMF)
几何分布的概率质量函数为:
$$ P(X = k) = (1 - p)^{k - 1} \cdot p, \quad \text{for } k = 1, 2, 3, \dots $$这表示:
- 第 $k-1$ 次都失败(概率为 $(1-p)^{k-1}$);
- 第 $k$ 次成功(概率为 $p$)。
📊 举个例子
比如你在抛一个不公平的硬币,正面(成功)的概率是 $p = 0.3$,你在等第一次出现正面:
- $P(X = 1) = 0.3$ (第一次就正面)
- $P(X = 2) = 0.7 \cdot 0.3 = 0.21$(第一次反面,第二次正面)
- $P(X = 3) = 0.7^2 \cdot 0.3 = 0.147$
📐 累积分布函数(CDF)
$$ P(X \leq k) = 1 - (1 - p)^k, k=1,2, \dots $$推导过程:
$$ F(k) = P(X \leq k) \\ = \sum^k_{i=1}P(X=i) \\ = \sum^k_{i=1}(1 - p)^{i - 1} \cdot p \\ = p\cdot\sum^k_{i=1}(1 - p)^{i - 1} $$令 $j=i-1$,则:
$$ F(k) = p\cdot\sum^k_{i=1}(1 - p)^{i - 1} \\ = p\cdot\sum^{k-1}_{j=0}(1 - p)^j \\ = p\cdot\frac{(1-p)^{k-1}-1}{(1-p)-p} \\ = 1-(1-p)^{k-1} $$🧠 解释直觉: 这个表达式表示,在前 $k$ 次试验中至少成功一次的概率。反过来说,所有前 $k$ 次都失败的概率是 $(1−p)^k$,所以 CDF 是:
$$ P(至少一次成功) = 1 - P(全部失败) = 1−(1−p)^k $$📈 期望
期望值(Mean):
$$ \mathbb{E}[X] = \frac{1}{p} $$🎯 推导期望 $\mathbb{E}[X]$
我们要计算:
$$ \mathbb{E}[X] = \sum_{k=1}^{\infty} k \cdot (1 - p)^{k-1} \cdot p $$令 $q = 1 - p$,则变为:
$$ \mathbb{E}[X] = p \sum_{k=1}^{\infty} k q^{k-1} $$这是一个经典级数:
$$ \sum_{k=1}^{\infty} k q^{k-1} = \frac{1}{(1 - q)^2} \quad \text{(当 } |q| < 1 \text{)} $$代入:
$$ \mathbb{E}[X] = p \cdot \frac{1}{(1 - q)^2} = p \cdot \frac{1}{p^2} = \frac{1}{p} $$📈 方差
方差(Variance):
$$ \text{Var}(X) = \frac{1 - p}{p^2} $$📊 推导方差 $\mathrm{Var}(X)$
我们使用公式:
$$ \mathrm{Var}(X) = \mathbb{E}[X^2] - \left(\mathbb{E}[X]\right)^2 $$1️⃣ 推导 $\mathbb{E}[X^2]$
我们要算:
$$ \mathbb{E}[X^2] = \sum_{k=1}^{\infty} k^2 \cdot q^{k-1} \cdot p = p \cdot \sum_{k=1}^{\infty} k^2 q^{k-1} $$这是一个已知级数(你可以从公式手册中找到):
$$ \sum_{k=1}^{\infty} k^2 q^{k-1} = \frac{1 + q}{(1 - q)^3} $$代入得:
$$ \mathbb{E}[X^2] = p \cdot \frac{1 + q}{(1 - q)^3} = p \cdot \frac{1 + (1 - p)}{p^3} = p \cdot \frac{2 - p}{p^3} = \frac{2 - p}{p^2} $$2️⃣ 代入方差公式
$$ \mathrm{Var}(X) = \mathbb{E}[X^2] - (\mathbb{E}[X])^2 = \frac{2 - p}{p^2} - \left( \frac{1}{p} \right)^2 = \frac{2 - p - 1}{p^2} = \frac{1 - p}{p^2} $$💡 应用场景举例
- 抛硬币直到第一次正面
- 某机器第一次成功响应的次数
- 网络中等待第一个成功包到达
- 马尔科夫链中的第一次跳转时间
🧠 小结
| 属性 | 几何随机变量 |
|---|---|
| 类型 | 离散型 |
| 取值 | 正整数 $\{1,2,3,\dots\}$ |
| 核心思想 | 第一次成功的试验编号 |
| PMF | $P(X = k) = (1 - p)^{k - 1} \cdot p$ |
| CDF | $1 - (1 - p)^k$ |
| 期望 | $\frac{1}{p}$ |
| 方差 | $\frac{1-p}{p^2}$ |
| 采样 | 模拟伯努利序列,或用反函数采样法 |
参考:
- Wiki: Geometric distribution
- ProofWiki: Geometric Distribution Gives Rise to Probability Mass Function
- Stackexchange: Solving for the CDF of the Geometric Probability Distribution
- ProofWiki: Expectation of Geometric Distribution
- ProofWiki: Variance of Geometric Distribution
import matplotlib.pyplot as plt
import numpy as np
import scipy.stats as stats
# 设置随机种子以保证结果可重复
np.random.seed(42)
# 1. 定义参数
p = 0.3
values = np.arange(1, 15)
n = len(values)
pmf = stats.geom(p).pmf(values)
cdf = np.cumsum(pmf) # 累积分布函数
# 2. 抽样
n_samples = 1000
samples = np.random.geometric(p=p, size=n_samples)
# 3. 可视化:理论分布 + 采样频率对比
plot_discrete_rv(values, pmf, cdf, samples, f"Geometric(p={p})")
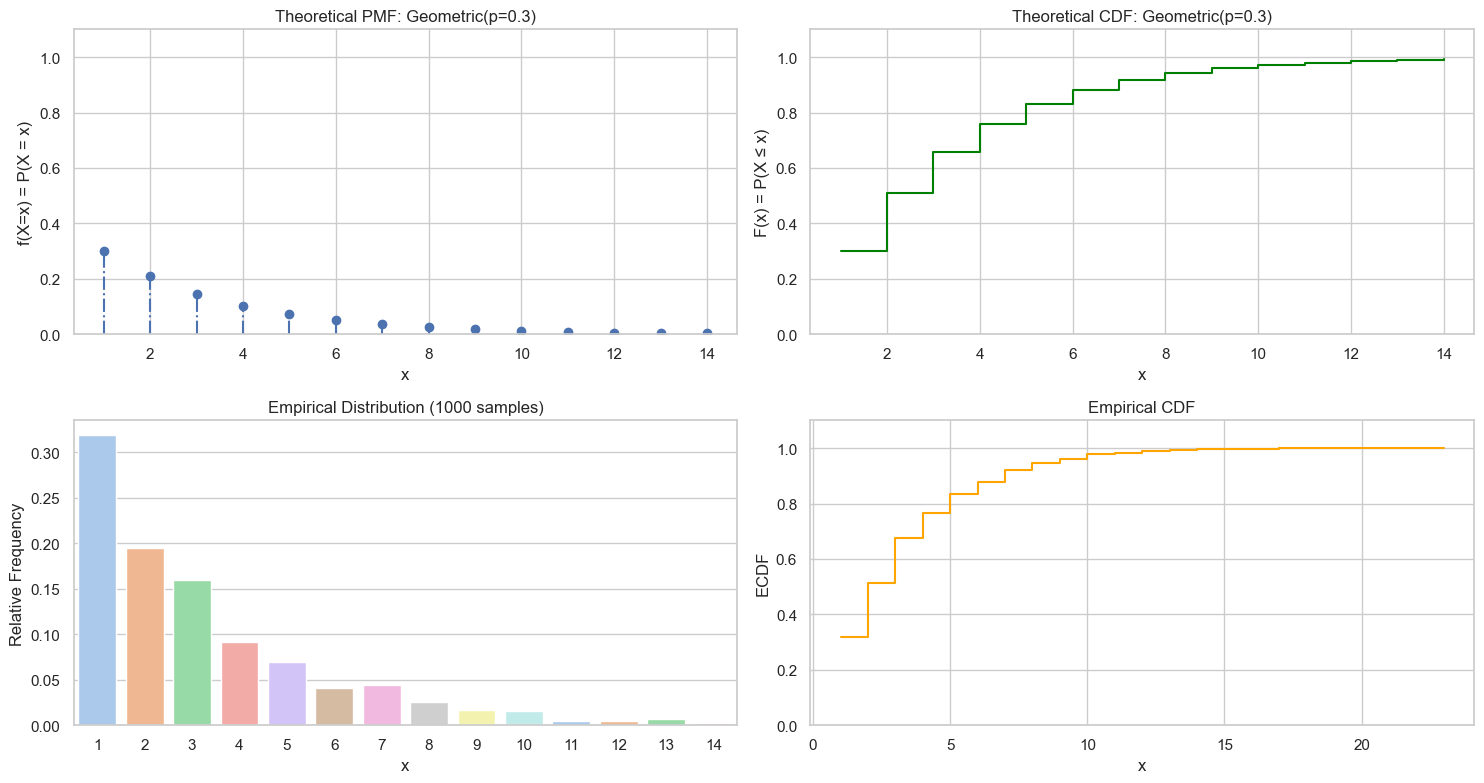
采样
采样方法对比
| 方法 | 原理 | 效率 | 优缺点 |
|---|---|---|---|
| 伯努利模拟 | 模拟每次试验 | 低 | 直观但慢,适合教学 |
| 反函数采样 | CDF 反函数 | 高 | 适合数学背景好者 |
| 查表法 | CDF + 查找 | 高 | 重复采样快,需预处理 |
| NumPy 内建 | 高效算法 | 高 | 工程实用,但略黑箱 |
import matplotlib.pyplot as plt
from scipy import stats
def verify_geometric_sample(p, samples):
"""
验证几何分布采样的正确性
:param p: 成功概率
:param samples: 采样结果列表(值域应为 1, 2, 3, ...)
:return: None
"""
N = len(samples)
# 均值与方差验证
empirical_mean = sum(samples) / N
theoretical_mean = 1 / p
print(f"Empirical mean: {empirical_mean:.3f}, Theoretical mean: {theoretical_mean:.3f}")
empirical_variance = sum((x - empirical_mean) ** 2 for x in samples) / N
theoretical_variance = (1 - p) / (p ** 2)
print(f"Empirical variance: {empirical_variance:.3f}, Theoretical variance: {theoretical_variance:.3f}")
# 统计最大值作为绘图范围
k_max = max(samples)
ks = list(range(1, k_max + 1))
# 统计频率(经验 PMF)
from collections import Counter
counter = Counter(samples)
counts = [counter.get(k, 0) / N for k in ks]
# 理论 PMF
theoretical = stats.geom(p).pmf(ks)
# 可视化
plt.figure(figsize=(10, 6))
plt.bar([k - 0.2 for k in ks], counts, width=0.4, label='Sampled Frequency', color='skyblue', align='center')
plt.bar([k + 0.2 for k in ks], theoretical, width=0.4, label='Theoretical PMF', color='orange', align='center')
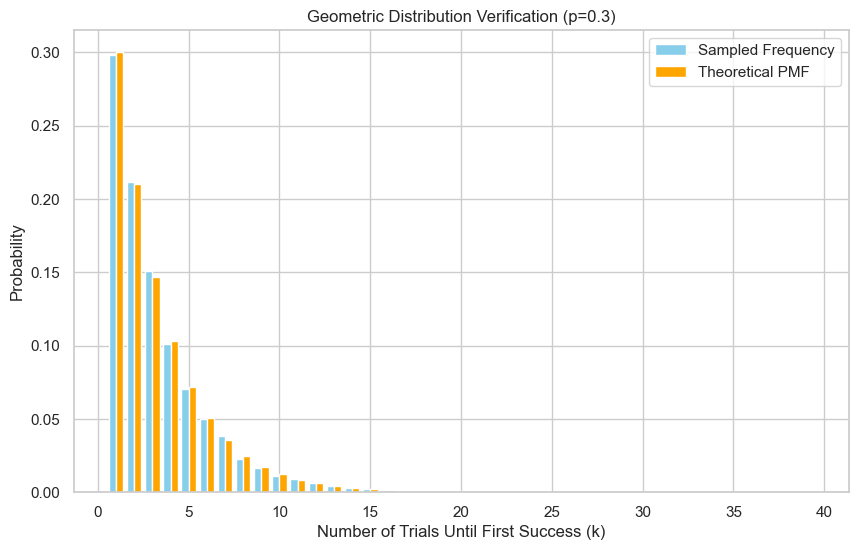
plt.xlabel("Number of Trials Until First Success (k)")
plt.ylabel("Probability")
plt.title(f"Geometric Distribution Verification (p={p})")
plt.legend()
plt.grid(True)
plt.show()
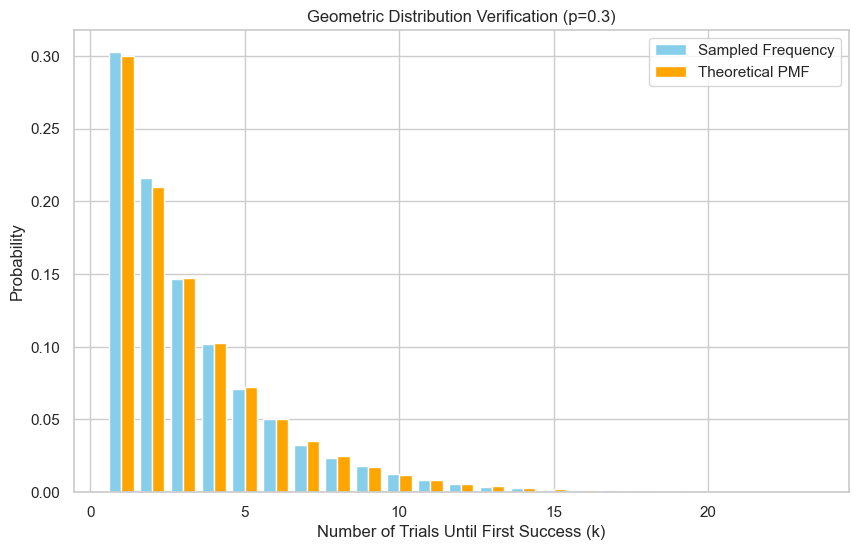
方法 1:利用 NumPy 内置函数
NumPy 已内置 Geometric 分布采样
- ✅ 优点:高性能、简洁
- ❌ 缺点:适合工程使用,学习原理时不推荐直接使用
import numpy as np
p = 0.3
n = 10000 # 采样次数
samples = np.random.geometric(p=p, size=n).tolist()
verify_geometric_sample(p, samples)
Empirical mean: 3.276, Theoretical mean: 3.333
Empirical variance: 7.363, Theoretical variance: 7.778
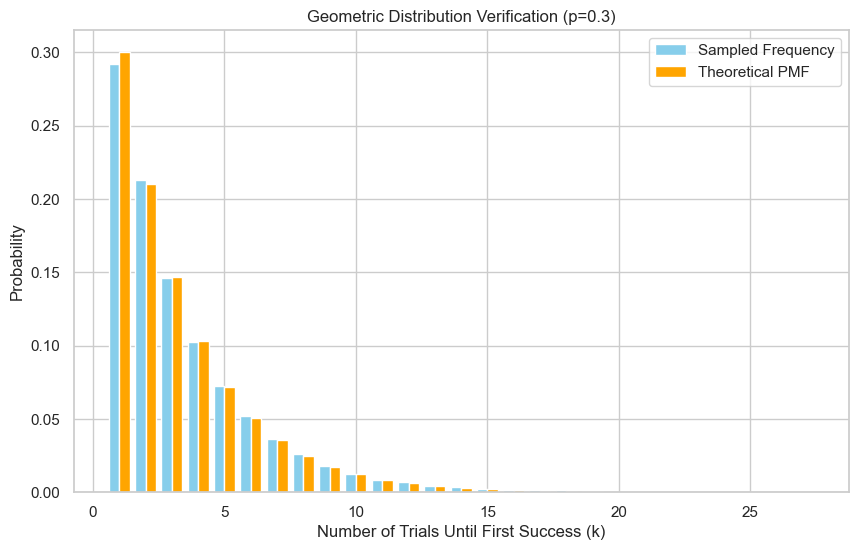
方法 2:反函数采样法
几何分布有一个封闭形式(close-form)的 CDF,因此可以使用反函数采样法(inverse transform sampling):
$$ X = \left\lceil \frac{\log(1 - U)}{\log(1 - p)} \right\rceil \quad \text{其中 } U \sim \text{Uniform}(0, 1) $$原理:
利用 Geometric 分布的 CDF($F(x) \sim \text{Uniform}(0,1)$):
$$ F(k) = 1 - (1 - p)^k $$如果我们从 $U \sim \text{Uniform}(0,1)$ 中得到一个值 $u$,那么有 $1-(1-p)^{i-1} \lt u \le 1-(1-p)^{i} $,其中,$i$ 就是我们要的采样值。我们可以推导出一个封闭形式:
$$ 1-(1-p)^{i-1} \lt u \le 1-(1-p)^{i} \\ -1+(1-p)^{i-1} \gt -u \ge -1+(1-p)^{i} \\ (1-p)^{i-1} \gt 1-u \ge (1-p)^{i} \\ ln((1-p)^{i-1}) \gt ln(1-u) \ge ln((1-p)^{i}) \\ (i-1)\cdot ln(1-p) \gt ln(1-u) \ge i\cdot ln(1-p) \\ i-1 \lt \frac{ln(1-u)}{ln(1-p)} \le i $$因此,$i = int(\frac{ln(1-u)}{ln(1-p)}) + 1$,其中,$int$ 表示实数部分的整数部分
即:
$$ k = \left\lceil \frac{\log(1 - U)}{\log(1 - p)} \right\rceil $$其中 $U \sim \text{Uniform}(0,1)$
$$ k = \left\lceil \frac{\log(U)}{\log(1 - p)} \right\rceil $$实际中,因为 $1 - U$ 与 $U$ 在分布上一致,所以常写为:
优劣:
- ✅ 优点:效率高,单次采样常数时间
- ✅ 适合低 $p$ 值时使用
- ❌ 缺点:需要计算对数函数,可能略慢于查表法
def sample_geometric_inverse(p):
"""
使用逆变换法采样几何分布
:param p: 成功概率
:return: 采样结果
"""
u = np.random.uniform(0, 1) # 从 [0, 1) 中采样一个均匀变量
return int(np.ceil(np.log(1 - u) / np.log(1 - p))) # 使用逆变换公式
def sample_geometric_inverse_list(p, n_samples):
"""
生成几何分布的采样列表
:param p: 成功概率
:param n_samples: 采样数量
:return: 采样结果列表
"""
return [sample_geometric_inverse(p) for _ in range(n_samples)]
p = 0.3
n = 10000 # 采样次数
samples = sample_geometric_inverse_list(p, n)
verify_geometric_sample(p, samples)
Empirical mean: 3.396, Theoretical mean: 3.333
Empirical variance: 8.143, Theoretical variance: 7.778
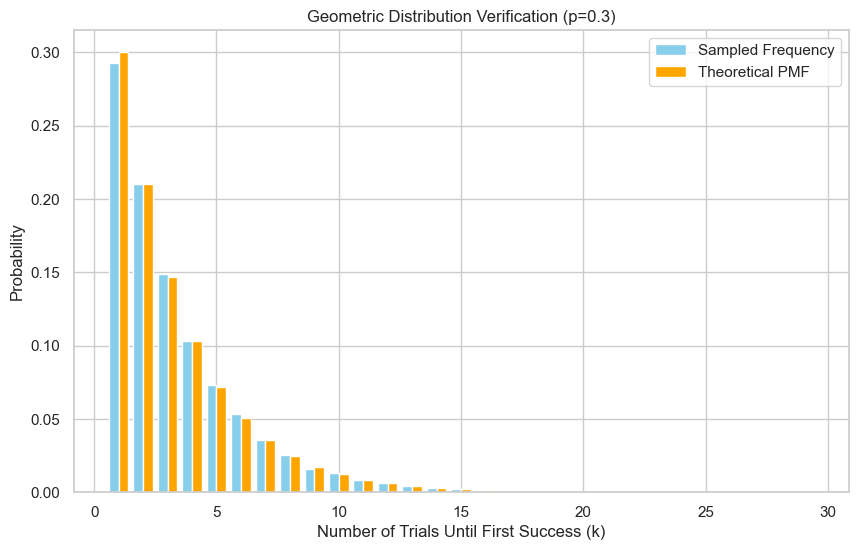
方法 3:查表法(CDF Table Lookup)
原理: 提前构建 CDF 表(PMF 累加),再用 Uniform 变量查找对应区间。
步骤:
- 给定 $p$,计算前 $N$ 个概率和 $\text{CDF}(k)$
- 生成 $U \sim \text{Uniform}(0, 1)$
- 找到最小的 $k$,使得 $\text{CDF}(k) \geq U$
优劣:
- ✅ 优点:采样快速(O(N) 或更快如二分查找)
- ✅ 适合重复采样场景
- ❌ 缺点:需要预存 CDF 表(内存占用)
import random
def build_cdf_table(p, max_k=100):
cdf = []
total = 0.0
for k in range(1, max_k + 1):
prob = (1 - p) ** (k - 1) * p
total += prob
cdf.append(total)
return cdf
def sample_geometric_lookup(cdf_table):
u = random.random()
for i, value in enumerate(cdf_table):
if u <= value:
return i + 1
return len(cdf_table) # fallback
def sample_geometric_lookup_list(p, n_samples, max_k=100):
cdf_table = build_cdf_table(p, max_k)
return [sample_geometric_lookup(cdf_table) for _ in range(n_samples)]
p = 0.3
n = 10000 # 采样次数
samples = sample_geometric_lookup_list(p, n)
verify_geometric_sample(p, samples)
Empirical mean: 3.371, Theoretical mean: 3.333
Empirical variance: 7.935, Theoretical variance: 7.778
方法 4:伯努利试验模拟法(Bernoulli Trial Simulation)
原理:从 $X \sim \text{Geometric}(p)$ 的定义出发:它表示第一个成功出现的位置。因此,只要重复投掷伯努利(p)分布的硬币,直到第一次出现“成功”(即为 1)。
步骤:
- 初始化计数器 $k = 1$
- 重复生成 $U \sim \text{Uniform}(0, 1)$
- 如果 $1-p \le U \le 1$,表示成功,返回 $k$
- 否则 $k \leftarrow k + 1$,重复
优劣:
- ✅ 优点:原理直观,适合教学演示
- ❌ 缺点:当 $p$ 很小时,可能需要很多次迭代,效率低
import random
def sample_geometric_mimic(p):
"""
模拟几何分布采样
:param p: 成功概率
:return: 采样结果
"""
k = 1
while True:
u = random.random() # 从 [0, 1) 中采样一个均匀变量
if 1-p <=u <=1: # 成功
return k
k += 1 # 失败,增加计数
def sample_geometric_mimic_list(p, n_samples):
"""
生成几何分布的采样列表
:param p: 成功概率
:param n_samples: 采样数量
:return: 采样结果列表
"""
return [sample_geometric_mimic(p) for _ in range(n_samples)]
# 采样
p = 0.3
N = 10000 # 采样次数
samples = sample_geometric_mimic_list(p, N)
verify_geometric_sample(p, samples)
Empirical mean: 3.339, Theoretical mean: 3.333
Empirical variance: 7.983, Theoretical variance: 7.778
正态随机变量(Normal Random Variables)
基础知识
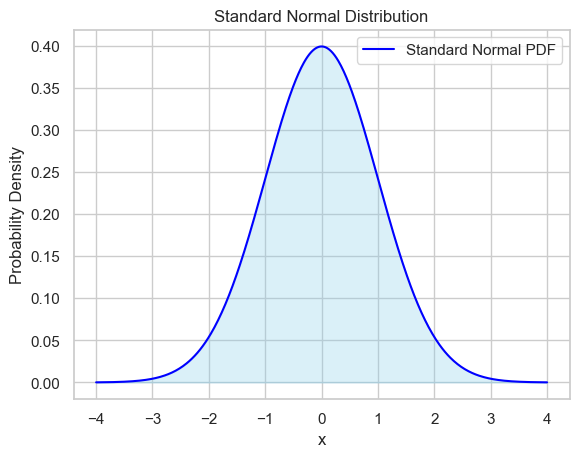
正态分布(Normal Distribution),也叫高斯分布,是一种连续型概率分布,在统计学中非常重要,是中心极限定理的核心分布。它的曲线呈钟形对称,在自然界与工程领域中频繁出现。
📐 概率密度函数(PDF)
正态分布的概率密度函数如下:
$$ f(x; \mu, \sigma) = \frac{1}{\sqrt{2\pi \sigma^2}} \exp\left(-\frac{(x - \mu)^2}{2\sigma^2}\right) $$- $\mu$:均值(位置参数,决定峰值中心)
- $\sigma^2$:方差(尺度参数,决定曲线宽度)
- $\sigma$:标准差
特殊情况:标准正态分布
当 $\mu = 0, \sigma = 1$ 时:
$$ f(x) = \frac{1}{\sqrt{2\pi}} \exp\left(-\frac{x^2}{2}\right) $$📈 形状与特性
对称性:关于 $\mu$ 对称
单峰性:均值处最高点
左右尾巴无限延伸,但总面积为 1
68-95-99.7 规则(经验法则):
- 约 68% 的概率集中在 $\mu \pm \sigma$
- 约 95% 的概率集中在 $\mu \pm 2\sigma$
- 约 99.7% 的概率集中在 $\mu \pm 3\sigma$
🧮 期望与方差的推导(标准正态)
- 期望:
- 方差:
这些推导需要用到对称性和高斯积分技巧(如换元法或配方法)。
🧪 正态分布的来源与直觉理解:中心极限定理(CLT)
多个独立随机变量的平均值在 n 趋于无穷大时趋于正态分布,无论原始分布是什么。
令 $\{X_{1},\ldots ,X_{n}\}$ 是一个独立同分布(i.i.d)的随机变量序列,它们满足的分布的期望值为$\mu$,方差为 $\sigma ^{2}$。
那么,其样本均值为:${\bar {X}}_{n}\equiv {\frac {X_{1}+\cdots +X_{n}}{n}}$。根据大数定理,
这也是为什么正态分布在自然现象中如此普遍:温度、身高误差、测量误差、考试成绩等。
🧠 应用场景
- 测量误差建模
- 机器学习中的高斯假设
- 贝叶斯推理中的先验 / 似然
- 股票收益建模(粗略)
- 数据生成 / 模拟 / MC 方法基础分布
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
x = np.linspace(-4, 4, 500)
pdf = norm.pdf(x, loc=0, scale=1)
plt.plot(x, pdf, label='Standard Normal PDF', color='blue')
plt.fill_between(x, pdf, alpha=0.3, color='skyblue')
plt.title("Standard Normal Distribution")
plt.xlabel("x")
plt.ylabel("Probability Density")
plt.grid(True)
plt.legend()
plt.show()
从标准正态随机变量(Standard Normal RV)中采样
标准正态分布是均值 $\mu = 0$,标准差 $\sigma = 1$ 的正态分布:
$$ f_Z(z) = \frac{1}{\sqrt{2\pi}} \exp\left(-\frac{z^2}{2}\right) $$| 方法 | 原理 | 是否推荐 | 是否快速 | 备注 |
|---|---|---|---|---|
np.random.normal | 内置库 | ✅ | ✅ | 最方便 |
| Box-Muller | 极坐标变换 | ✅ | ✅ | 原理直观,适合教学 |
| Inverse CDF | 反函数采样 | ❌ | ❌ | 无解析解,需近似或查表 |
| 中心极限定理 | 简单直观,教学友好,但精度有限,不适用于高精度模拟 | |||
| Rejection Sampling | 接受拒绝机制 | ⚠️ | ❌ | 通用性强,效率低 |
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
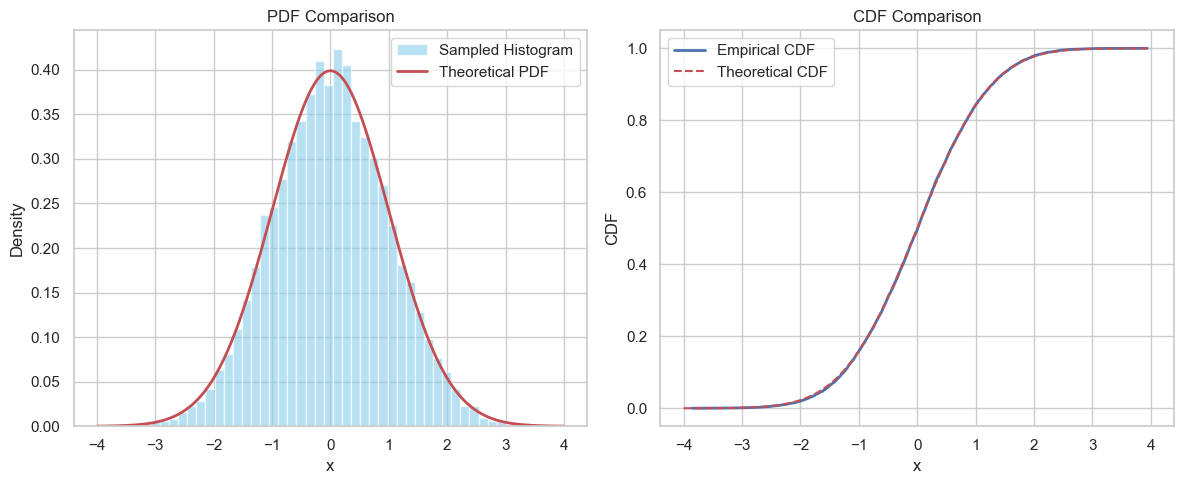
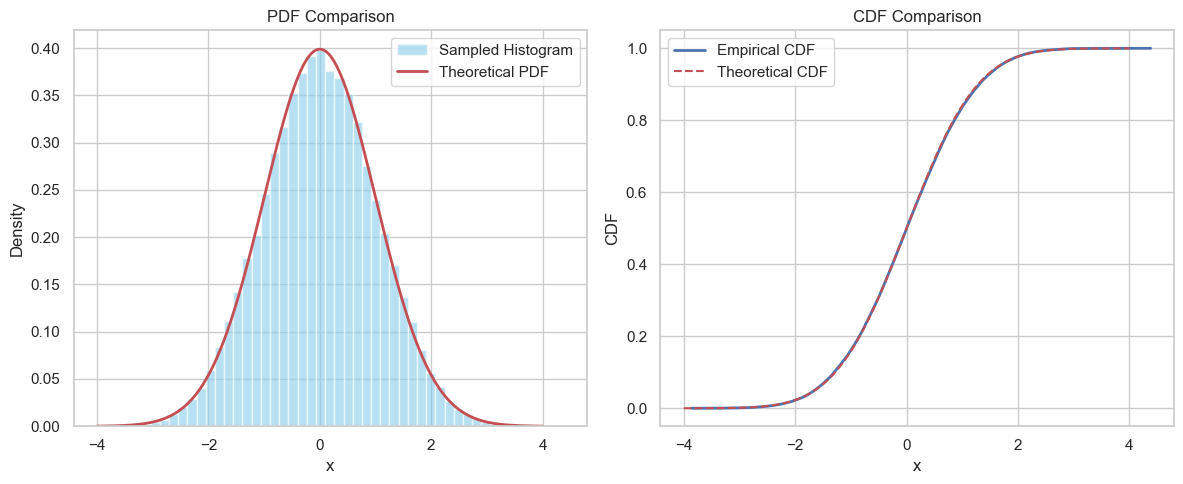
def verify_standard_normal_sample(samples):
"""
验证标准正态分布采样的正确性
:param samples: 从 N(0,1) 中采样的结果 (list or array)
"""
N = len(samples)
# 经验统计量
empirical_mean = np.mean(samples)
empirical_var = np.var(samples)
# 理论统计量
theoretical_mean = 0
theoretical_var = 1
print(f"Empirical mean: {empirical_mean:.4f} | Theoretical mean: {theoretical_mean}")
print(f"Empirical var: {empirical_var:.4f} | Theoretical var: {theoretical_var}")
# 直方图 + 理论 PDF
plt.figure(figsize=(12, 5))
plt.subplot(1, 2, 1)
x = np.linspace(-4, 4, 500)
plt.hist(samples, bins=50, density=True, alpha=0.6, color='skyblue', label='Sampled Histogram')
plt.plot(x, norm.pdf(x, loc=theoretical_mean, scale=np.sqrt(theoretical_var)), 'r-', lw=2, label='Theoretical PDF')
plt.title('PDF Comparison')
plt.xlabel('x')
plt.ylabel('Density')
plt.legend()
plt.grid(True)
# 经验 CDF vs 理论 CDF
plt.subplot(1, 2, 2)
sorted_samples = np.sort(samples)
empirical_cdf = np.arange(1, N+1) / N
plt.plot(sorted_samples, empirical_cdf, label='Empirical CDF', lw=2)
plt.plot(x, norm.cdf(x, loc=theoretical_mean, scale=np.sqrt(theoretical_var)), 'r--', label='Theoretical CDF')
plt.title('CDF Comparison')
plt.xlabel('x')
plt.ylabel('CDF')
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()
✅ 方法一:用 NumPy 直接采样(最方便)
import numpy as np
samples = np.random.normal(loc=0, scale=1, size=10000)
# verify the sampling results
verify_standard_normal_sample(samples)
Empirical mean: 0.0045 | Theoretical mean: 0
Empirical var: 0.9778 | Theoretical var: 1
✅ 方法二:Box-Muller 变换(经典方法)
Box-Muller 变换(Box-Muller transform)是一种从均匀分布采样两个变量,生成两个独立标准正态随机变量的方法。这个方法是构造性的、非近似的(不像中心极限定理那样是逼近)。
🧠 背后思想:
我们希望从两个独立的标准正态分布 $\mathcal{N}(0, 1)$ 中采样出变量 $Z_1$ 和 $Z_2$。
我们已知无法直接从正态分布中采样,但我们可以很容易地从均匀分布中采样两个变量 $U_1, U_2 \sim \text{Uniform}(0, 1)$,然后通过变量变换得到 $Z_1, Z_2$。
🧮 数学推导核心步骤
Step 1:将正态分布转为极坐标
2维独立标准正态分布的联合概率密度函数为:
$$ f_{XY}(x, y) = f_X(x)f_Y(y) = \frac{1}{\sqrt{2\pi}} e^{-\frac{x^2}{2}} \cdot \frac{1}{\sqrt{2\pi}} e^{-\frac{y^2}{2}} = \frac{1}{2\pi} e^{-\frac{x^2 + y^2}{2}} $$如果我们用极坐标表示 $x = r\cos\theta, y = r\sin\theta$,则:
$$ f(r, \theta) = f(x,y) \cdot |J| = \frac{1}{2\pi} e^{-\frac{r^2}{2}} \cdot r $$其中 $|J| = r$ 是雅可比行列式(面积拉伸),也就是说:
$$ f_{R,\Theta}(r, \theta) = \underbrace{r e^{-r^2/2}}_{\text{与 } r \text{ 有关}} \cdot \underbrace{\frac{1}{2\pi}}_{\text{与 } \theta \text{ 有关}} $$这表示 $R$ 和 $\Theta$ 是相互独立的随机变量!
所以联合 pdf 变成:
$$ f(r, \theta) = \frac{r}{2\pi} e^{-\frac{r^2}{2}} \quad \text{for } r \in [0, \infty), \theta \in [0, 2\pi) $$Step 2:构造采样变量
所以我们只需要想办法分别从以下两个分布中采样:
- $\Theta \sim \text{Uniform}(0, 2\pi)$
- $R \sim \text{PDF } f_R(r) = r e^{-r^2/2},\quad r \geq 0$
我们看 $R$ 的分布:
$$ f_R(r) = r e^{-r^2/2} $$对比:设 $U_1 \sim \text{Uniform}(0,1)$,我们令:
$$ R = \sqrt{-2 \ln U_1} $$我们可以反向验证:这个 R 的分布的概率密度函数正是:
$$ f_R(r) = \frac{d}{dr} \mathbb{P}(R \leq r) = \frac{d}{dr} \mathbb{P}(U_1 \geq e^{-r^2/2}) = \frac{d}{dr} \left( 1 - e^{-r^2/2} \right) = r e^{-r^2/2} $$所以这个变量变换是正确的。
另一方面,在二维正态联合分布下,角度方向是均匀的:
$$ f_\Theta(\theta) = \frac{1}{2\pi},\quad \theta \in [0, 2\pi) $$所以只需要一个均匀分布 $U_2 \sim \text{Uniform}(0,1)$,通过线性缩放即可:
$$ \Theta = 2\pi U_2 $$✅ 最终变换
将 $R = \sqrt{-2 \ln U_1}$,$\Theta = 2\pi U_2$ 带入:
$$ Z_1 = R \cos\Theta = \sqrt{-2 \ln U_1} \cdot \cos(2\pi U_2) \\ Z_2 = R \sin\Theta = \sqrt{-2 \ln U_1} \cdot \sin(2\pi U_2) $$这两个变量就是我们希望得到的独立标准正态变量。
📌 Box-Muller 的优点和缺点
| 优点 | 缺点 |
|---|---|
| 数学严谨,生成值精确服从正态分布 | 需要使用对数和三角函数,较慢 |
| 每次采样两个正态样本 | 不适合嵌入式设备、GPU 等需性能优化场合 |
| 适用于理解极坐标变换与正态分布的关系 | 不能高效矢量化为 SIMD 代码 |
🚀 小结
Box-Muller 是一个 理论完美 的标准正态分布采样方法,具有如下特点:
- 利用两个独立的 $U(0,1)$ 样本
- 构造两个 $\mathcal{N}(0,1)$ 独立样本
- 变换方式基于二维极坐标系统和雅可比推导
- 是一种标准的“从简单分布变换为复杂分布”的经典案例
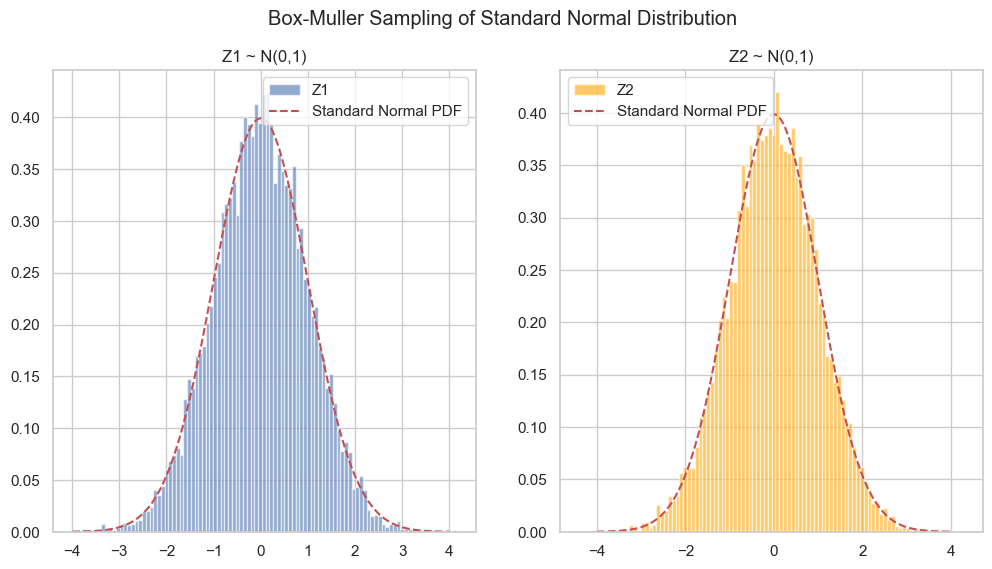
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
def box_muller_sample(n_samples=10000, visualize=True):
# Step 1: 生成两个均匀分布变量
U1 = np.random.uniform(0, 1, n_samples)
U2 = np.random.uniform(0, 1, n_samples)
# Step 2: Box-Muller变换
R = np.sqrt(-2 * np.log(U1))
theta = 2 * np.pi * U2
Z1 = R * np.cos(theta)
Z2 = R * np.sin(theta)
if visualize:
num_bins = 100
plt.figure(figsize=(12, 6))
plt.subplot(1, 2, 1)
plt.hist(Z1, bins=num_bins, density=True, alpha=0.6, label='Z1')
x = np.linspace(-4, 4, 500)
plt.plot(x, norm.pdf(x), 'r--', label='Standard Normal PDF')
plt.title("Z1 ~ N(0,1)")
plt.legend()
plt.subplot(1, 2, 2)
plt.hist(Z2, bins=num_bins, density=True, alpha=0.6, label='Z2', color='orange')
plt.plot(x, norm.pdf(x), 'r--', label='Standard Normal PDF')
plt.title("Z2 ~ N(0,1)")
plt.legend()
plt.suptitle("Box-Muller Sampling of Standard Normal Distribution")
plt.grid(True)
plt.show()
return Z1, Z2
box_muller_sample(n_samples=10000, visualize=True)
(array([ 1.48779139, 0.98464068, -0.80586692, ..., -0.52369914,
-0.56467099, -2.07728924], shape=(10000,)),
array([ 1.22339848, -0.80627553, 0.55483184, ..., -1.4385899 ,
2.53391275, -0.82037306], shape=(10000,)))
✅ 方法三:反函数采样法(理论可行,实际但不可行)
用反函数采样法:设 $U \sim \text{Uniform}(0,1)$,则令:
$$ Z = F^{-1}(U) $$其中 $F$ 是正态分布的 CDF,$F^{-1}$ 是它的反函数(即分位数函数 / probit 函数)。
问题:标准正态分布的 CDF 没有解析反函数,所以不能用基本函数表达,但可以通过查表或近似(如 Beasley-Springer 算法)。
✅ 方法四:利用中心极限定理(Central Limit Theorem, CLT) 进行采样
使用 中心极限定理(Central Limit Theorem, CLT) 进行采样,是一种经典且直观的方式来生成近似 标准正态分布 的样本。这种方法常用于教学演示,原理简单,但在实际高精度模拟中不常用。
🧠 Step-by-step:为什么 CLT 可以用来采样标准正态分布
我们以如下问题为目标:
能否通过一组简单的独立随机变量(例如均匀分布)来构造一个近似服从标准正态分布 $\mathcal{N}(0, 1)$ 的变量?
答案是:可以! 这就是中心极限定理的威力。
🎯 Step 1: 中心极限定理的核心内容
$$ Z_n = \frac{\sum_{i=1}^n X_i - n\mu}{\sqrt{n\sigma^2}} \xrightarrow{d} \mathcal{N}(0,1) $$中心极限定理(CLT): 假设你有一组独立同分布(i.i.d)的随机变量 $X_1, X_2, \dots, X_n$,每个变量的期望值为 $\mu$,方差为 $\sigma^2$。那么:
当 $n \to \infty$,这个标准化的和(或者平均值)在分布上趋近于标准正态分布。
📌 Step 2: 用均匀分布来举例说明
我们选一个简单的分布,例如 Uniform(0, 1) 分布:
- 它的期望 $\mu = 0.5$
- 它的方差 $\sigma^2 = \frac{1}{12}$
我们采样 $n$ 个这样的变量 $U_1, \dots, U_n$,然后构造如下变量:
$$ Z = \frac{\sum_{i=1}^n U_i - n\mu}{\sqrt{n\sigma^2}} = \frac{\sum_{i=1}^n (U_i - 0.5)}{\sqrt{n \cdot \frac{1}{12}}} $$也就是说:
$$ Z = \sum_{i=1}^n (U_i - 0.5) \cdot \sqrt{12 / n} $$这个变量 $Z$ 会越来越接近标准正态分布。
$n$的取值取决于所选择的分布。对于均匀分布,$n$的值可以很小就可以快速收敛。
🧪 Step 3: 实验演示构造过程
设 $n = 12$,那么:
$$ Z = \sum_{i=1}^{12} (U_i - 0.5) $$为什么乘 $\sqrt{12}$?
因为:
- 每个 $U_i - 0.5$ 是均值为 0、方差为 $1/12$ 的变量;
- 相加之后的和方差为 $n \cdot \frac{1}{12}$,
- 为了标准化(变成方差为 1 的变量),要乘以 $\frac{1}{\sqrt{n \cdot \frac{1}{12}}} = \sqrt{12 / n}$。
✨ 对于标准正态采样:
我们可以使用如下构造方式:
$$ Z = \frac{1}{\sqrt{n}} \sum_{i=1}^n (U_i - \mu) $$- $U_i \sim \text{Uniform}(a,b)$(或其他分布)
- $\mu$ 是 $U_i$ 的期望,例如对 $U(0,1)$ 是 $0.5$
- 当 $n$ 越大时,$Z \approx N(0,1)$
import numpy as np
def sample_normal_via_clt(a=0, b=1, n=12, num_samples=10000):
"""
利用中心极限定理从 Uniform(a, b) 采样生成近似标准正态分布的样本
:param a: Uniform 分布下界
:param b: Uniform 分布上界
:param n: 每次采样的 Uniform 个数
:param num_samples: 总共生成多少个样本
:return: 一个近似标准正态的样本数组
"""
# 计算均值和标准差
mu = (a + b) / 2
sigma = (b - a) / np.sqrt(12) # 均匀分布的标准差
# Step 1: 从 Uniform(a, b) 中生成 n 个样本,重复 num_samples 次
uniform_samples = np.random.uniform(a, b, size=(num_samples, n))
#print(uniform_samples.shape) #(num_samples, n)
# Step 2: 对每一组样本求和并标准化
sample_sums = np.sum(uniform_samples, axis=1) # (num_samples,)
z_samples = (sample_sums - n * mu) / (np.sqrt(n) * sigma)
return z_samples
samples = sample_normal_via_clt(a=0, b=1, n=10, num_samples=100000)
verify_standard_normal_sample(samples)
Empirical mean: 0.0034 | Theoretical mean: 0
Empirical var: 1.0084 | Theoretical var: 1
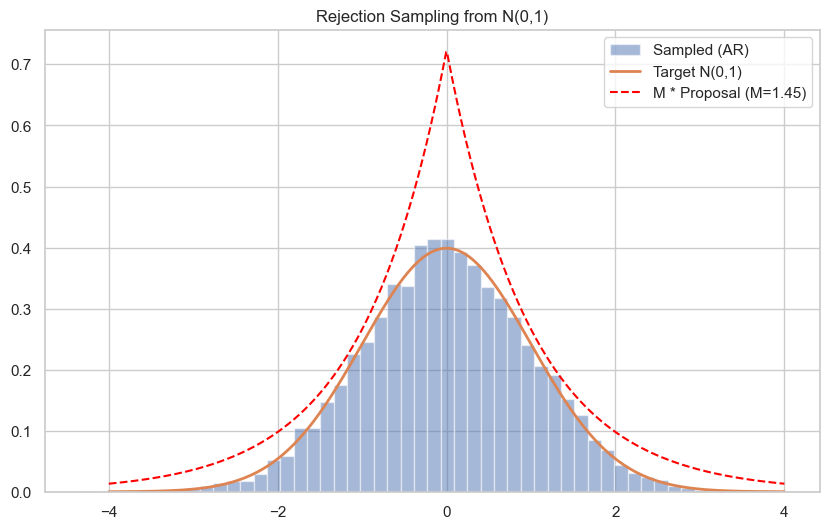
✅ 方法五:拒绝采样(Rejection Sampling)
- 使用易采样的 proposal 分布(如 Cauchy、Laplace 等),通过接受率控制生成标准正态。
- 不推荐新手一开始就用,但适合了解各种采样框架。
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm, laplace
# 目标分布: 标准正态
target_pdf = lambda x: norm.pdf(x)
# proposal: Laplace 分布
proposal_pdf = lambda x: laplace.pdf(x)
proposal_sampler = lambda size: laplace.rvs(size=size)
# M 是 f(x)/q(x) 的上界,估计为最大值(略大于实际最大)
x_vals = np.linspace(-10, 10, 1000)
M = np.max(target_pdf(x_vals) / proposal_pdf(x_vals)) * 1.1
# 采样函数
def rejection_sample(n):
samples = []
while len(samples) < n:
x = proposal_sampler(1)[0]
u = np.random.uniform()
if u < target_pdf(x) / (M * proposal_pdf(x)):
samples.append(x)
return np.array(samples)
# 生成样本
samples = rejection_sample(10000)
# 可视化
x = np.linspace(-4, 4, 1000)
plt.figure(figsize=(10,6))
plt.hist(samples, bins=50, density=True, alpha=0.5, label="Sampled (AR)")
plt.plot(x, norm.pdf(x), label="Target N(0,1)", lw=2)
plt.plot(x, M * proposal_pdf(x), '--', label=f"M * Proposal (M={M:.2f})", color="red")
plt.title("Rejection Sampling from N(0,1)")
plt.legend()
plt.grid(True)
plt.show()
随机变量的计算
随机变量变换(Random Variable Transformation)
线性变换
🎯 问题描述
设:
- $X$ 是一个连续型随机变量,已知其概率密度函数(pdf)为 $f_X(x)$,
- $a \neq 0$, $b \in \mathbb{R}$ 是常数,
- 定义 $Y = aX + b$,
- 求 $Y$ 的概率密度函数 $f_Y(y)$。
🧠 基本原理
这是单调变换下的密度函数变换规则:
$$ f_Y(y) = f_X\left( \frac{y - b}{a} \right) \cdot \left| \frac{1}{a} \right| $$⚠️ 注意绝对值符号是因为 $a$ 有可能是负数。
📌 推导过程
我们来系统推导一下这个公式。
第一步:从CDF出发
先求出 $Y$ 的 CDF(累积分布函数):
- 如果 $a > 0$:
然后对 $y$ 求导:
$$ f_Y(y) = \frac{d}{dy} F_X\left( \frac{y - b}{a} \right) = f_X\left( \frac{y - b}{a} \right) \cdot \frac{1}{a} $$- 如果 $a < 0$:
然后:
$$ f_Y(y) = \frac{d}{dy} \left[ 1 - F_X\left( \frac{y - b}{a} \right) \right] = -f_X\left( \frac{y - b}{a} \right) \cdot \frac{1}{a} $$因为 $a < 0$,所以结果仍然是:
$$ f_Y(y) = f_X\left( \frac{y - b}{a} \right) \cdot \left| \frac{1}{a} \right| $$✅ 结论(变换公式)
不管 $a > 0$ 还是 $a < 0$,统一公式为:
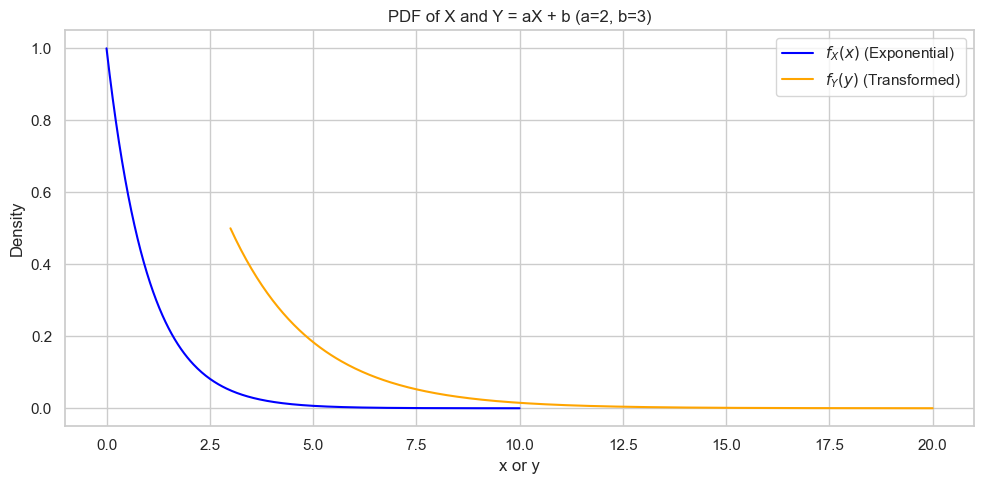
$$ \boxed{ f_Y(y) = f_X\left( \frac{y - b}{a} \right) \cdot \left| \frac{1}{a} \right| } $$🧪 示例:$X \sim \text{Exponential}(\lambda)$,$Y = 2X + 3$
原始 pdf:
$$ f_X(x) = \lambda e^{-\lambda x}, \quad x \geq 0 $$令 $Y = 2X + 3$,那么:
- $a = 2$, $b = 3$
- $ f_Y(y) = f_X\left( \frac{y - 3}{2} \right) \cdot \frac{1}{2} = \lambda e^{-\lambda \cdot \frac{y - 3}{2}} \cdot \frac{1}{2}, \quad y \geq 3$
import numpy as np
import matplotlib.pyplot as plt
# Parameters
lambda_ = 1 # parameter for Exponential distribution
a = 2
b = 3
# Define the original PDF of X ~ Exp(lambda)
def f_X(x):
return lambda_ * np.exp(-lambda_ * x) * (x >= 0)
# Define the transformed PDF of Y = aX + b
def f_Y(y):
x = (y - b) / a
return f_X(x) * (1 / abs(a)) * (y >= b)
# Create x and y ranges
x_vals = np.linspace(0, 10, 400)
y_vals = np.linspace(3, 20, 400)
# Evaluate PDFs
fx_vals = f_X(x_vals)
fy_vals = f_Y(y_vals)
# Plot
plt.figure(figsize=(10, 5))
plt.plot(x_vals, fx_vals, label=r'$f_X(x)$ (Exponential)', color='blue')
plt.plot(y_vals, fy_vals, label=r'$f_Y(y)$ (Transformed)', color='orange')
plt.title('PDF of X and Y = aX + b (a=2, b=3)')
plt.xlabel('x or y')
plt.ylabel('Density')
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()
非线性变换(nonlinear transformation)
非常好!讨论**非线性变换(nonlinear transformation)**是理解概率论与统计推理的关键部分。我们分步骤深入讲解:
🧠 问题:非线性变换下如何求随机变量的分布?
设:
- $X$ 是一个已知连续型随机变量,有密度函数 $f_X(x)$
- 定义新变量:$Y = g(X)$,其中 $g$ 是一个 可微的、严格单调的函数
我们想要求出 $Y$ 的概率密度函数 $f_Y(y)$。
🧮 理论结果:变换法公式
对于单调可微函数 $g$,有:
$$ f_Y(y) = f_X\big(g^{-1}(y)\big) \cdot \left| \frac{d}{dy} g^{-1}(y) \right| $$这个公式被称作变换法(Change of Variables)或反函数法(Inverse Method)。
✅ 步骤总结(以单调递增函数为例)
- 写出 $Y = g(X)$
- 推出反函数 $X = g^{-1}(Y)$
- 计算反函数的导数 $\frac{d}{dy} g^{-1}(y)$
- 将这些代入变换公式,得出 $f_Y(y)$
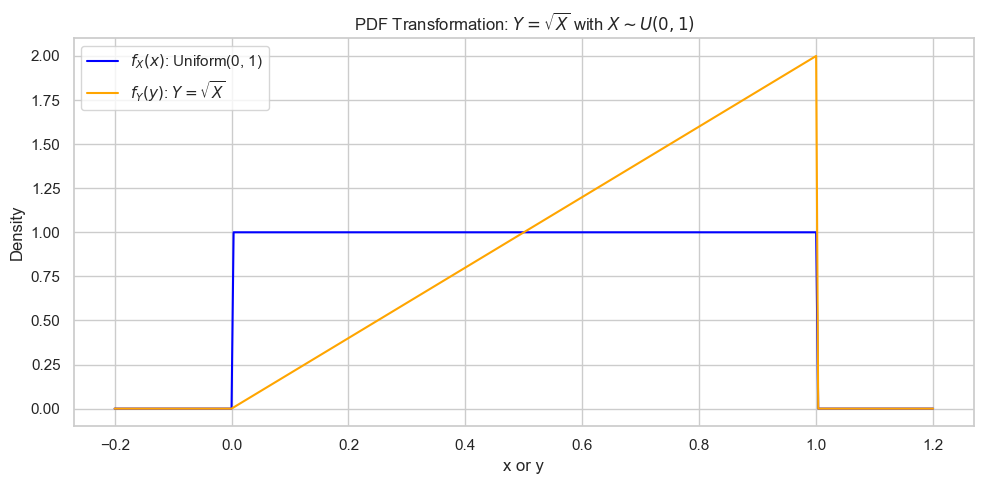
📌 举例:$Y = \sqrt{X}$,其中 $X \sim \text{Uniform}(0, 1)$
我们来一步一步操作这个变换。
- 原始变量:
- 非线性变换:
- 求导:
- 代入公式:
定义域:
- 因为 $X \in [0, 1] \Rightarrow Y \in [0, 1]$
所以:
$$ f_Y(y) = \begin{cases} 2y, & 0 \le y \le 1 \\ 0, & \text{otherwise} \end{cases} $$这是一个三角形形状的密度函数!
import numpy as np
import matplotlib.pyplot as plt
# Define the original PDF: X ~ Uniform(0, 1)
def f_X(x):
return np.ones_like(x) * ((x >= 0) & (x <= 1))
# Define the transformation: Y = sqrt(X) => X = Y^2
def f_Y(y):
return 2 * y * ((y >= 0) & (y <= 1))
# Create value ranges
x_vals = np.linspace(-0.2, 1.2, 400)
y_vals = np.linspace(-0.2, 1.2, 400)
# Evaluate PDFs
fx_vals = f_X(x_vals)
fy_vals = f_Y(y_vals)
# Plot the PDFs
plt.figure(figsize=(10, 5))
plt.plot(x_vals, fx_vals, label=r'$f_X(x)$: Uniform(0, 1)', color='blue')
plt.plot(y_vals, fy_vals, label=r'$f_Y(y)$: $Y = \sqrt{X}$', color='orange')
plt.title("""PDF Transformation: $Y = \sqrt{X}$ with $X \sim U(0, 1)$""")
plt.xlabel('x or y')
plt.ylabel('Density')
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()
<>:24: SyntaxWarning: invalid escape sequence '\s'
<>:24: SyntaxWarning: invalid escape sequence '\s'
/var/folders/mx/684cy0qs5zd3c_pdx4wy4pkc0000gn/T/ipykernel_15262/4117088612.py:24: SyntaxWarning: invalid escape sequence '\s'
plt.title("""PDF Transformation: $Y = \sqrt{X}$ with $X \sim U(0, 1)$""")
期望运算符(Mean Operator)
基础
🔍 什么是 Mean Operator?
“Mean operator”是指对随机变量取期望的运算符。 在概率论中,我们通常使用符号:
$$ \mathbb{E}[X] $$来表示随机变量 $X$ 的期望(也称平均值、期望值、均值)。 这个运算可以看成是对随机变量在其分布下的“加权平均”。
📊 离散型随机变量的期望
如果 $X$ 是一个离散型随机变量,取值为 $x_1, x_2, \dots$,概率为 $P(X = x_i) = p_i$, 那么其期望为:
$$ \mathbb{E}[X] = \sum_{i} x_i \cdot p_i $$例子:
投一枚公平的硬币,令 $X = 1$ 表示正面,$X = 0$ 表示反面:
$$ \mathbb{E}[X] = 1 \cdot \frac{1}{2} + 0 \cdot \frac{1}{2} = \frac{1}{2} $$📈 连续型随机变量的期望
如果 $X$ 是一个连续随机变量,具有概率密度函数(PDF) $f_X(x)$, 那么其期望为:
$$ \mathbb{E}[X] = \int_{-\infty}^{\infty} x \cdot f_X(x) \, dx $$例子:
若 $X \sim \text{Uniform}(0, 1)$,即 $f_X(x) = 1$ for $x \in [0, 1]$,则:
$$ \mathbb{E}[X] = \int_0^1 x \cdot 1 \, dx = \left[ \frac{1}{2}x^2 \right]_0^1 = \frac{1}{2} $$🔁 Mean Operator vs 实际平均
期望是理论上的平均值,是对整个概率分布而言的。而现实中我们往往只能观察到有限的样本:
$$ \bar{x} = \frac{1}{n} \sum_{i=1}^{n} x_i $$这叫做样本均值(sample mean),它是用来近似估计 $\mathbb{E}[X]$ 的。根据大数定律,当样本数量趋近于无穷大时,样本均值会收敛到理论期望。
🧮 Mean Operator 的性质(线性)
设 $X, Y$ 是随机变量,$a, b$ 是常数,则:
- 线性性(Linearity):
- 恒等函数的期望:
对于函数的期望
设 $X$ 是一个随机变量,我们希望计算 $g(X)$ 的期望:
$$ \mathbb{E}[g(X)] $$✅ 离散型推导
假设 $X$ 是离散型随机变量,取值集合为 $\{x_1, x_2, \dots, x_n\}$,概率质量函数为 $p(x_i) = P(X = x_i)$。
我们要计算 $\mathbb{E}[g(X)]$,意思是对每个可能的取值 $x_i$,取函数值 $g(x_i)$,再乘以其出现的概率,再加总起来。
🔍 推导:
$$ \mathbb{E}[g(X)] = \sum_{i=1}^{n} g(x_i) \cdot P(X = x_i) $$✅ 本质是“对随机变量函数值的加权平均”,权重就是其发生概率。
✅ 连续型推导:
设 $X$ 是连续型随机变量,其概率密度函数为 $f_X(x)$,我们希望计算 $\mathbb{E}[g(X)]$。
🔍 推导:
我们可以使用积分的方式,将所有可能的 $x$ 上的 $g(x)$ 值进行加权平均,权重是 $f_X(x)$:
$$ \mathbb{E}[g(X)] = \int_{-\infty}^{\infty} g(x) \cdot f_X(x) \, dx $$✅ 本质上仍然是“加权平均”:对每个可能的 $x$,用密度函数给出的权重。
📌 举例讲解
例子一:🎲 离散型例子。
设 $X$ 是掷一个四面骰子的结果(均匀离散分布),取值为 $\{1,2,3,4\}$,每个概率 $p(x) = 1/4$。
我们定义 $g(X) = X^2$,计算其期望:
$$ \mathbb{E}[X^2] = \sum_{x=1}^{4} x^2 \cdot \frac{1}{4} = \frac{1}{4}(1^2 + 2^2 + 3^2 + 4^2) = \frac{1}{4}(1 + 4 + 9 + 16) = \frac{30}{4} = 7.5 $$例子二:📈 连续型例子。
设 $X \sim \text{Uniform}(0, 1)$,密度函数 $f_X(x) = 1$ for $x \in [0, 1]$。
取函数 $g(x) = x^2$,计算:
$$ \mathbb{E}[X^2] = \int_0^1 x^2 \cdot 1 \, dx = \left[ \frac{x^3}{3} \right]_0^1 = \frac{1}{3} $$🔁 与直接期望的区别
- $\mathbb{E}[X]$:是原始随机变量的期望;
- $\mathbb{E}[g(X)]$:是对 $X$ 做函数变换后的期望,不等于 $g(\mathbb{E}[X])$(除非 $g$ 是线性函数)!
例如上例中:
- $\mathbb{E}[X] = 0.5$,
- $g(x) = x^2$,
- $g(\mathbb{E}[X]) = (0.5)^2 = 0.25 \neq \mathbb{E}[X^2] = \frac{1}{3}$
📚 总结
| 类型 | 定义 | 公式 |
|---|---|---|
| 离散型 | $\mathbb{E}[g(X)] = \sum g(x_i) \cdot P(X = x_i)$ | 加权平均 |
| 连续型 | $\mathbb{E}[g(X)] = \int g(x) \cdot f_X(x) \, dx$ | 加权积分 |
误差传播法则(Propagation Laws)
Propagation laws(误差传播定律),也叫作uncertainty propagation,是指当你通过某个函数 $Y = g(X_1, X_2, \dots, X_n)$ 来计算一个变量时,如果输入变量 $X_i$ 都有不确定性(通常以方差或标准差表示),那么我们想知道输出变量 $Y$ 的不确定性是多少。
这套理论的核心是如何推导:
$$ \text{Var}(Y) \quad \text{或者} \quad \sigma_Y $$✅ 一元情形(只有一个变量)
] 设 $Y = g(X)$,而 $X$ 是一个随机变量,均值 $\mu_X$,方差 $\sigma_X^2$,
如果 $g$ 是光滑函数(可微),并且 $X$ 的波动不大,可以使用一阶泰勒展开近似:
$$ Y \approx g(\mu_X) + g'(\mu_X)(X - \mu_X) $$于是可以近似得到:
$$ \boxed{\text{Var}(Y) \approx \left(g'(\mu_X)\right)^2 \cdot \text{Var}(X)} $$✅ 多元情形(多个输入变量)
设输出变量:
$$ Y = g(X_1, X_2, \dots, X_n) $$我们可以展开一阶泰勒展开式:
$$ Y \approx g(\boldsymbol{\mu}) + \sum_{i=1}^{n} \frac{\partial g}{\partial x_i} (X_i - \mu_i) $$于是得到方差的近似传播式:
$$ \boxed{\text{Var}(Y) \approx \sum_{i=1}^{n} \left(\frac{\partial g}{\partial x_i}\right)^2 \cdot \text{Var}(X_i) + 2 \sum_{i < j} \frac{\partial g}{\partial x_i} \cdot \frac{\partial g}{\partial x_j} \cdot \text{Cov}(X_i, X_j)} $$- 如果 $X_1, \dots, X_n$ 独立,协方差项为 0,简化为:
📐 示例讲解
🎯 例子 1:乘法传播
设 $Y = XY$,其中 $X \sim N(\mu_X, \sigma_X^2)$,$Y \sim N(\mu_Y, \sigma_Y^2)$,且 $X, Y$ 独立。
- $g(X, Y) = XY$
我们有:
- $\frac{\partial g}{\partial X} = Y$
- $\frac{\partial g}{\partial Y} = X$
代入传播公式(用期望近似导数):
$$ \text{Var}(XY) \approx (\mu_Y)^2 \sigma_X^2 + (\mu_X)^2 \sigma_Y^2 $$📊 例子 2:温度换算(线性变换)
摄氏温度 $C \sim N(\mu, \sigma^2)$,换算成华氏温度:
$$ F = 1.8 C + 32 $$由于是线性变换,直接使用公式:
$$ \text{Var}(F) = (1.8)^2 \cdot \text{Var}(C) $$📌 小结表格
| 形式 | 描述 |
|---|---|
| 一元变换 | $\text{Var}(Y) \approx (g'(\mu))^2 \cdot \text{Var}(X)$ |
| 多元独立变量 | $\text{Var}(Y) \approx \sum (\partial g / \partial x_i)^2 \cdot \text{Var}(X_i)$ |
| 多元相关变量 | 加上协方差项 |
| 线性变换 | 精确成立:$Y = aX + b \Rightarrow \text{Var}(Y) = a^2 \cdot \text{Var}(X)$ |
⚠️ 注意事项
- 该方法是近似方法,准确性取决于函数在局部的线性程度;
- 适用于输入误差较小的情况;
- 更高阶误差可以用二阶泰勒展开改进;
- 若分布不是正态分布,结果依然是近似的。
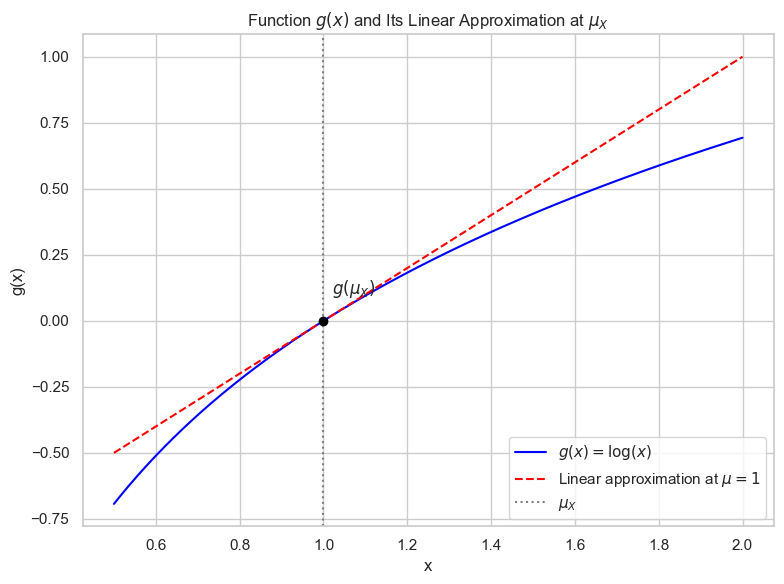
为什么可以用 X 在均值附近的线性近似?
我们说:
$$ g(X) \approx g(\mu_X) + g'(\mu_X)(X - \mu_X) $$设随机变量 $X$ 有均值 $\mu_X$,函数 $Y = g(X)$, 那么我们可以用 X 在均值附近的线性近似:
你问的是:这一步为什么可以这么做?有什么依据?
✅ 这一步其实是使用了“泰勒一阶展开”(Taylor Expansion)
🌟 1. 什么是泰勒展开?
泰勒展开是用一个函数在某点的导数信息,近似表示这个函数在附近的值。
对一个可导函数 $g(x)$,在点 $x = a$ 处进行泰勒展开,有:
$$ g(x) = g(a) + g'(a)(x - a) + \frac{g''(a)}{2!}(x - a)^2 + \cdots $$如果我们只保留一阶项(也就是导数那一项),就叫:
$$ \boxed{ g(x) \approx g(a) + g'(a)(x - a) } \quad \text{(一阶泰勒展开)} $$🌟 2. 为什么在误差传播里这么用?
设 $X$ 是一个带噪声的输入量,我们知道它的均值是 $\mu_X$,方差是 $\sigma_X^2$,但它总有一些波动。
我们关心的是:当 $X$ 在 $\mu_X$ 附近波动时,输出 $Y = g(X)$ 会怎样波动?
于是我们在 $\mu_X$ 附近进行线性近似:
$$ g(X) \approx g(\mu_X) + g'(\mu_X)(X - \mu_X) $$这个式子的意义是:
- $g(\mu_X)$:是平均输出
- $g'(\mu_X)(X - \mu_X)$:是输入 $X$ 波动带来的线性变化
这种线性逼近在 $X$ 变动不大的时候是很合理的 —— 就像我们画图时用直线近似曲线的一小段。
📈 图像直观理解
- 画一条函数曲线 $y = g(x)$,比如 $g(x) = \log x$
- 在 $x = \mu_X$ 画一条切线
- 看看这条切线在附近是否与原函数差不多
这就是泰勒展开的一阶逼近,它告诉我们:
如果你只关心“函数在平均点附近是怎么变的”,那么只看导数(斜率)就足够。
🔍 为什么一阶就足够?
因为我们关注的是方差的传播:
- 方差只取决于函数的一阶变化速度,即 $g'(x)$;
- 如果你保留高阶项,比如 $(x - \mu)^2$,你需要知道高阶导数,分析会复杂很多;
- 在误差很小(即 $X$ 的波动很小)时,一阶项就主导了误差传播的行为。
✅ 总结一句话:
我们用:
$$ g(X) \approx g(\mu_X) + g'(\mu_X)(X - \mu_X) $$是因为:
- 这是一阶泰勒展开,用于在 $\mu_X$ 附近逼近函数;
- 当输入误差很小时,这是非常好的近似;
- 这个逼近能帮助我们分析输出 $Y$ 的波动(即方差)是如何由输入 $X$ 的波动造成的。
import numpy as np
import matplotlib.pyplot as plt
# 定义非线性函数和它的导数
def g(x):
return np.log(x)
def g_prime(x):
return 1 / x
# 取均值点 mu
mu = 1.0
x = np.linspace(0.5, 2.0, 400)
# 原函数值
y = g(x)
# 一阶线性近似:在 mu 附近
y_approx = g(mu) + g_prime(mu) * (x - mu)
# 绘图
plt.figure(figsize=(8, 6))
plt.plot(x, y, label=r'$g(x) = \log(x)$', color='blue')
plt.plot(x, y_approx, '--', label='Linear approximation at $\mu=1$', color='red')
plt.axvline(mu, color='gray', linestyle=':', label=r'$\mu_X$')
# 标记点
plt.scatter([mu], [g(mu)], color='black', zorder=5)
plt.text(mu+0.02, g(mu)+0.1, r'$g(\mu_X)$', fontsize=12)
plt.title('Function $g(x)$ and Its Linear Approximation at $\mu_X$')
plt.xlabel('x')
plt.ylabel('g(x)')
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()
<>:24: SyntaxWarning: invalid escape sequence '\m'
<>:31: SyntaxWarning: invalid escape sequence '\m'
<>:24: SyntaxWarning: invalid escape sequence '\m'
<>:31: SyntaxWarning: invalid escape sequence '\m'
/var/folders/mx/684cy0qs5zd3c_pdx4wy4pkc0000gn/T/ipykernel_15262/692038390.py:24: SyntaxWarning: invalid escape sequence '\m'
plt.plot(x, y_approx, '--', label='Linear approximation at $\mu=1$', color='red')
/var/folders/mx/684cy0qs5zd3c_pdx4wy4pkc0000gn/T/ipykernel_15262/692038390.py:31: SyntaxWarning: invalid escape sequence '\m'
plt.title('Function $g(x)$ and Its Linear Approximation at $\mu_X$')
样本均值算子(Sample mean operator)
在统计中,sample mean operator 就是将一个随机变量的若干个独立样本求平均的操作:
给定某个随机变量 $X$,我们从中独立采样 $n$ 个样本:
$$ X_1, X_2, \dots, X_n \sim \text{i.i.d. from } X $$则样本均值(sample mean)定义为:
$$ \bar{X}_n = \frac{1}{n} \sum_{i=1}^{n} X_i $$这个操作就叫做 sample mean operator:它接受一个样本序列,输出平均值。
Sample mean operator 是从数据中估计总体均值的最基本工具,具有无偏性、方差随样本数降低、集中性和正态性等重要性质。
📌 sample mean 的重要性质
1. 无偏性(Unbiasedness)
$$ \mathbb{E}[\bar{X}_n] = \mathbb{E}\left[\frac{1}{n} \sum_{i=1}^n X_i\right] = \frac{1}{n} \sum_{i=1}^n \mathbb{E}[X_i] = \mu $$👉 说明:样本均值是总体均值的无偏估计。
2. 方差
$$ \mathrm{Var}[\bar{X}_n] = \frac{1}{n^2} \sum_{i=1}^n \mathrm{Var}[X_i] = \frac{\sigma^2}{n} $$👉 意义:样本均值的方差随着样本数增加而减小。
3. 集中性(大数定律)
根据大数定律(Law of Large Numbers):
$$ \bar{X}_n \xrightarrow{a.s.} \mu \quad \text{as } n \to \infty $$👉 意义:样本均值几乎必然收敛到总体均值。
4. 近似正态分布(中心极限定理)
当 $n$ 很大时,根据中心极限定理:
$$ \bar{X}_n \approx \mathcal{N}\left(\mu, \frac{\sigma^2}{n} \right) $$👉 意义:无论原始分布如何,样本均值在大样本下近似服从正态分布。
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(42)
# 假设原始分布 X 是指数分布(不是正态)
X = np.random.exponential(scale=1.0, size=(10000,)) # 原始样本
# 不同样本数量下的 sample mean
sample_sizes = [1, 5, 10, 30, 100]
means = []
for n in sample_sizes:
sample_means = [np.mean(np.random.choice(X, n, replace=False)) for _ in range(1000)]
means.append(sample_means)
# 可视化不同 n 下的 sample mean 分布
fig, axs = plt.subplots(1, len(sample_sizes), figsize=(18, 3))
for i, n in enumerate(sample_sizes):
axs[i].hist(means[i], bins=30, color='skyblue', edgecolor='black', density=True)
axs[i].set_title(f'n={n}')
axs[i].axvline(np.mean(X), color='red', linestyle='--', label='True Mean')
axs[i].legend()
plt.suptitle('Sample Mean Distribution as Sample Size Increases')
plt.tight_layout()
plt.show()

利用 sample mean operator 来近似计算一些无法解析求解的积分
这其实就是蒙特卡洛积分(Monte Carlo Integration)的核心思想。我们可以利用 sample mean operator 来近似计算一些无法解析求解的积分,特别是在高维或复杂函数情形下。
🧠 思路总览:用样本均值近似积分
设我们想计算一个积分:
$$ I = \int_a^b f(x)\,dx $$若这个积分无法解析求出,可以把它看成期望:
$$ I = (b - a) \cdot \mathbb{E}_{X \sim \mathcal{U}(a, b)}[f(X)] $$其中,$X$ 是均匀随机变量
✅ 为什么可以这样变?
如果 $X \sim \mathcal{U}(a, b)$,那么它的密度是:
$$ p(x) = \frac{1}{b-a}, \quad x \in [a, b] $$所以:
$$ \mathbb{E}[f(X)] = \int_a^b f(x) \cdot p(x)\,dx = \int_a^b f(x) \cdot \frac{1}{b-a} \, dx = \frac{1}{b-a} \int_a^b f(x)\,dx $$整理得:
$$ \int_a^b f(x)\,dx = (b - a) \cdot \mathbb{E}[f(X)] $$📌 用样本均值近似期望
我们可以从 $X \sim \mathcal{U}(a, b)$ 中采样 $n$ 个样本 $x_1, x_2, \dots, x_n$,计算:
$$ \mathbb{E}[f(X)] \approx \frac{1}{n} \sum_{i=1}^{n} f(x_i) $$因此:
$$ \int_a^b f(x)\,dx \approx \frac{b - a}{n} \sum_{i=1}^n f(x_i) $$📚 拓展:为什么这很有用?
在高维空间或复杂积分(比如贝叶斯推断中),没有解析解时:
- 你无法用牛顿积分;
- 你可以只依赖样本!
✅ 总结一句话
通过把积分转化为期望,我们可以利用 sample mean operator 和均匀采样来近似任何无法解析求解的积分 —— 这就是蒙特卡洛积分的核心。
✅ Python 实现:Monte Carlo 积分
我们来试试计算:
$$ I = \int_0^1 e^{-x^2}\,dx $$这里,
- $a = 0, b = 1$
- $f(x) = e^{-x^2}$
这是无法解析求出的(其实这就是误差函数 erf 的一部分),但我们可以数值估算它。
import numpy as np
import matplotlib.pyplot as plt
# 被积函数
def f(x):
return np.exp(-x**2)
# 积分区间
a, b = 0, 1
# Monte Carlo 采样数量
n = 10000
x_samples = np.random.uniform(a, b, n) # 1️⃣ 均匀采样 [a, b] 区间
# 样本均值估计
estimate = (b - a) * np.mean(f(x_samples)) # 2️⃣ 计算样本均值并乘以区间长度
print(f"[Estimate Value] Monte Carlo estimate of ∫₀¹ e^(-x²) dx ≈ {estimate:.6f}")
# 计算真实值
from scipy.special import erf
true_val = np.sqrt(np.pi)/2 * erf(1)
print(f"[True Value] The true value of ∫₀¹ e^(-x²) dx ≈ {true_val:.6f}")
[Estimate Value] Monte Carlo estimate of ∫₀¹ e^(-x²) dx ≈ 0.743534
[True Value] The true value of ∫₀¹ e^(-x²) dx ≈ 0.746824
采样方法(Sample Methods)
又见:
反函数法(Inverse Transform Sampling)
给定概率密度/质量函数 $f_X(x)$,则:
- 计算 $F_X(x)$
- 基于均匀随机变量获得一个值
- 计算 $F_X^{-1}(u)$ 从而得到 $x$。这个 $x$ 就是我们想要的采样值。
想象你画了 CDF 曲线 $F_X(x)$,横轴是$x$,纵轴是概率$[0,1]$。
- 随机生成一个 $u \in [0,1]$
- 找到这个 $u$ 在 CDF 上对应的横坐标:这就是你要的样本 $x$
注意:
当我们已经知道了CDF,并且可以从这个CDF获得一个封闭形式(close form)的函数,就可以使用这个方法
import numpy as np
import plotly.graph_objs as go
from plotly.subplots import make_subplots
# 目标分布:指数分布 X ~ Exp(λ=1)
x_vals = np.linspace(0, 6, 500)
cdf_vals = 1 - np.exp(-x_vals) # CDF of Exp(1)
inv_cdf = lambda u: -np.log(1 - u) # x = 反函数 F⁻¹(u)
# 随机采样 5 个均匀数
np.random.seed(42)
u_samples = np.sort(np.random.uniform(0, 1, 5))
x_samples = inv_cdf(u_samples)
# 创建子图:左侧显示 CDF 映射过程,右侧显示 Histogram
fig = make_subplots(rows=1, cols=2,
subplot_titles=("Inverse Transform Sampling", "Histogram of Transformed Samples"),
column_widths=[0.6, 0.4])
# 左图:CDF 曲线
fig.add_trace(go.Scatter(x=x_vals, y=cdf_vals, mode='lines', name='CDF F(x)', line=dict(color='blue')),
row=1, col=1)
# 添加每个 u 值的水平线和对应的 x 映射
for u, x in zip(u_samples, x_samples):
fig.add_trace(go.Scatter(x=[0, x], y=[u, u], mode='lines',
line=dict(dash='dot', color='gray'), showlegend=False), row=1, col=1)
fig.add_trace(go.Scatter(x=[x], y=[u], mode='markers+text',
marker=dict(color='red', size=8),
text=[f"x={x:.2f}"], textposition='top right', showlegend=False), row=1, col=1)
# 添加 u 样本点
fig.add_trace(go.Scatter(x=[0]*len(u_samples), y=u_samples, mode='markers',
marker=dict(symbol='line-ns-open', color='green', size=10),
name='u ~ Uniform(0,1)'), row=1, col=1)
# 右图:x 样本的直方图
fig.add_trace(go.Histogram(x=x_samples, nbinsx=10, name='Sampled X', marker_color='orange'), row=1, col=2)
# 布局设置
fig.update_layout(height=500, width=900, title_text="Inverse Transform Sampling Visualization (Exponential RV)",
showlegend=True)
fig.update_xaxes(title_text="x", row=1, col=1)
fig.update_yaxes(title_text="F(x) or u", row=1, col=1)
fig.update_xaxes(title_text="Sampled x", row=1, col=2)
fig.update_yaxes(title_text="Frequency", row=1, col=2)
fig.show()
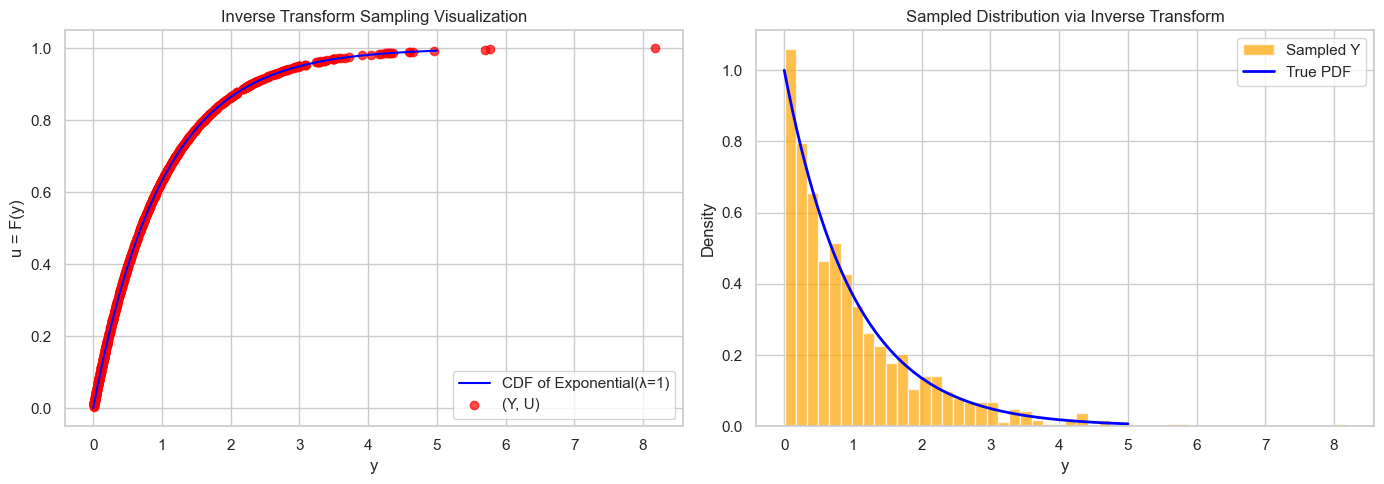
为什么我们可以用均匀分布来采样其他任意分布(比如伯努利、指数、正态等)
这背后的理论基础是 概率论中关于 分布函数(CDF)和其反函数的性质。核心思想是:概率积分变换(Probability Integral Transform)
定理(概率积分变换 / Probability Integral Transform):
若随机变量 $X$ 的分布函数是 $F_X(x)$,且 $F_X$ 是严格单调的连续函数,那么 $U = F_X(X) \sim \text{Uniform}(0,1)$, 反过来,$X = F_X^{-1}(U)$ 也服从原始分布 $X$。
换句话说:
- 你可以把任何分布的采样问题,变成 Uniform(0,1) 的采样问题 + 一个反函数变换。
🧠 为什么这个成立?
我们来直观推导一下第二个方向(也是我们用来“生成任意分布”的方向):
假设:
- $U \sim \text{Uniform}(0,1)$
- 设 $Y = F^{-1}(U)$,我们想证明 $Y \sim F$
证明:
我们来计算 $Y = F^{-1}(U)$ 的 CDF,也就是:
$$ P(Y \leq y) $$由于 $Y = F^{-1}(U)$,那么:
$$ P(Y \leq y) = P(F^{-1}(U) \leq y) $$✅ 第一步:运用反函数的单调性
前提条件:$F$ 是连续、严格递增的函数(这是保证反函数存在并单调的关键)。
所以我们可以对不等式 $F^{-1}(U) \leq y$ 应用函数 $F$,变成:
$$ F^{-1}(U) \leq y \quad \Leftrightarrow \quad U \leq F(y) $$这是非常关键的一步!我们把 “关于 $Y$” 的事件 转化成了 “关于 $U$” 的事件。
✅ 第二步:使用 $U \sim \text{Uniform}(0,1)$
$$ P(U \leq F(y)) = F(y) $$为什么呢?因为:
- $U \sim \text{Uniform}(0,1)$
- 所以 $P(U \leq u) = u$,对于 $u \in [0,1]$
- 而 $F(y) \in [0,1]$,因为 $F$ 是一个合法的分布函数
所以:
$$ P(U \leq F(y)) = F(y) $$✅ 综合起来:
$$ P(Y \leq y) = P(F^{-1}(U) \leq y) = P(U \leq F(y)) = F(y) $$因此,$Y$ 的分布函数就是 $F$,所以我们说 $Y \sim F$。
🎯 应用举例:
伯努利采样:
如果 $U < p$,我们就输出 1,否则输出 0,相当于:
$$ F^{-1}(u) = \begin{cases} 1 & u < p \\ 0 & u \ge p \end{cases} $$
指数分布采样:
- Exponential 的 CDF 是 $F(x) = 1 - e^{-\lambda x}$
- 反函数是 $F^{-1}(u) = -\frac{1}{\lambda} \ln(1 - u)$
💡 直觉总结
你可以把 Uniform(0,1) 理解为“抽签”,然后用每种分布的分布函数告诉我们这个“抽签号”对应什么“事件”或“数值”。
📊 为什么我们要这样做?
- Uniform(0,1) 是最容易模拟的分布:几乎所有语言都有
random()。 - 如果能把任何分布转化为 Uniform,就能统一采样流程,简化算法设计。
- 用在:蒙特卡洛方法、MCMC、生成模型、仿真系统……
import numpy as np
import matplotlib.pyplot as plt
# Target distribution: Exponential(lambda=1)
from scipy.stats import expon
# Generate Uniform samples
n = 1000
U = np.random.uniform(0, 1, n)
U_sorted = np.sort(U)
# Compute inverse CDF (quantile function) for exponential
Y = expon.ppf(U_sorted)
# Prepare plot
fig, axs = plt.subplots(1, 2, figsize=(14, 5))
# Plot CDF of Exponential
x = np.linspace(0, 5, 500)
cdf = expon.cdf(x)
axs[0].plot(x, cdf, label='CDF of Exponential(λ=1)', color='blue')
axs[0].scatter(Y, U_sorted, color='red', alpha=0.7, label='(Y, U)')
axs[0].set_title('Inverse Transform Sampling Visualization')
axs[0].set_xlabel('y')
axs[0].set_ylabel('u = F(y)')
axs[0].legend()
axs[0].grid(True)
# Plot histogram of sampled Y
axs[1].hist(Y, bins=50, density=True, alpha=0.7, color='orange', label='Sampled Y')
axs[1].plot(x, expon.pdf(x), color='blue', lw=2, label='True PDF')
axs[1].set_title('Sampled Distribution via Inverse Transform')
axs[1].set_xlabel('y')
axs[1].set_ylabel('Density')
axs[1].legend()
axs[1].grid(True)
plt.tight_layout()
plt.show()
离散型反函数采样
反函数法(Inverse Transform Sampling) 并不只适用于连续型随机变量,它同样适用于离散型随机变量,原理是类似的,只是操作略有不同。下面我将详细为你讲解离散型随机变量上的应用。
而对于离散分布,$F_X(x)$ 是阶梯函数(跳跃),我们不能用“解析反函数”,但可以通过查找法实现“反函数”的效果。
🧮 离散型反函数采样:核心步骤
我们通过累积概率表来代替反函数,主要流程如下:
有一个离散型 RV $X$,其可能取值为 $x_1, x_2, ..., x_n$,概率为 $p_1, p_2, ..., p_n$
构造其 累积分布函数(CDF):
$$ F(x_k) = \sum_{i=1}^k p_i $$从 $u \sim \text{Uniform}(0, 1)$ 中采样
找到第一个使得 $F(x_k) \geq u$ 的 $x_k$,这就是采样值
✅ 示例:采样离散变量 X,其中:
- $P(X=1) = 0.1$
- $P(X=2) = 0.3$
- $P(X=3) = 0.4$
- $P(X=4) = 0.2$
那么 CDF 为:
| 值 $x$ | 概率 $p$ | 累积 $F(x)$ |
|---|---|---|
| 1 | 0.1 | 0.1 |
| 2 | 0.3 | 0.4 |
| 3 | 0.4 | 0.8 |
| 4 | 0.2 | 1.0 |
如果你采到 $u = 0.75$,你会落在 $F(x=3)=0.8$,所以输出 3; 如果 $u = 0.85$,你会输出 4。
✅ 总结
| 对象类型 | 是否能用反函数法? | 如何实现? |
|---|---|---|
| 连续型 RV | ✅ 是 | 用解析或数值方式计算 $F^{-1}(u)$ |
| 离散型 RV | ✅ 是 | 用查找 + 累积分布函数模拟 $F^{-1}(u)$ |
采样离散分布
采样一个二维有限离散型随机变量(2D Finite Discrete Random Variable)
采样一个二维有限离散型随机变量(2D Finite Discrete Random Variable),本质上就是从一个给定的联合概率分布表 $P(X = x_i, Y = y_j)$ 中生成随机样本对 $(x_i, y_j)$。
✅ 总结
| 方法 | 原理 | 适用场景 | |
|---|---|---|---|
| 展平联合分布 + 反函数采样 | 一维化处理所有 $(x,y)$ 对 | 联合概率矩阵已知 | |
| 边缘 + 条件采样 | 先采 $X$,再采 (Y | X) | 更复杂/结构化的模型 |
✅ 方法一:展平+反函数采样
核心思路:
将二维联合分布展平为一维,然后做累积概率表 + 反函数采样(Inverse CDF Sampling)。
🔢 步骤:
- 创建所有可能的值对 $(x_i, y_j)$;
- 展平联合概率表 $P(x_i, y_j)$;
- 构造累积分布函数(CDF);
- 从 $[0,1]$ 上采样 $u$,找第一个 $u \leq \text{CDF}[k]$;
- 返回对应的 $(x_i, y_j)$。
✅ 假设你已有联合分布表
比如:
| y=0 | y=1 | y=2 | |
|---|---|---|---|
| x=0 | 0.1 | 0.2 | 0.1 |
| x=1 | 0.1 | 0.2 | 0.1 |
| x=2 | 0.05 | 0.05 | 0.1 |
这个二维分布的总概率是 1。
import numpy as np
import random
def flatten_joint_distribution(x_vals, y_vals, joint_probs):
"""
展平二维联合分布矩阵
:param joint_probs: 二维联合分布矩阵
:return: 展平后的概率分布
"""
# 展平联合分布
flattened = joint_probs.flatten()
#print("Flatten joint probabilities:", flattened)
# 所有可能的(x, y)组合(顺序与flattened一致)
xy_pairs = [(x, y) for x in x_vals for y in y_vals]
#print("XY pairs:", xy_pairs)
return flattened, xy_pairs
def sample_2d_discrete_inverse_transform(x_vals, y_vals, joint_probs):
# flatten the joint distribution
flattened, xy_pairs = flatten_joint_distribution(x_vals, y_vals, joint_probs)
# apply inverse transform sampling
cdf = np.cumsum(flattened)
u = random.random()
for i, threshold in enumerate(cdf):
if u <= threshold:
return xy_pairs[i]
return xy_pairs[-1] # fallback for u ~ 1.0
import numpy as np
import matplotlib.pyplot as plt
# 定义二维离散联合分布
x_vals = [0, 1, 2]
y_vals = [0, 1, 2]
joint_probs = np.array([
[0.1, 0.2, 0.1],
[0.1, 0.2, 0.1],
[0.05, 0.05, 0.1]
]) # shape (3, 3)
assert np.isclose(joint_probs.sum(), 1.0), "Joint probabilities must sum to 1"
# 采样
N = 1000 # 采样次数
samples = [sample_2d_discrete_inverse_transform(x_vals, y_vals, joint_probs) for _ in range(N)]
x_sample, y_sample = zip(*samples)
# 可视化联合频率
import seaborn as sns
import pandas as pd
df = pd.DataFrame({'x': x_sample, 'y': y_sample})
pivot_table = pd.crosstab(df['x'], df['y'], normalize='all')
plt.figure(figsize=(15, 5))
plt.subplot(1, 2, 1)
sns.heatmap(joint_probs, annot=True, cmap="YlGnBu", fmt=".3f", xticklabels=y_vals, yticklabels=x_vals)
plt.title("Theoretical Joint Distribution from Samples")
plt.xlabel("Y")
plt.ylabel("X")
plt.subplot(1, 2, 2)
sns.heatmap(pivot_table, annot=True, cmap="YlGnBu", fmt=".3f", xticklabels=y_vals, yticklabels=x_vals)
plt.title("Empirical Joint Distribution from Samples")
plt.xlabel("Y")
plt.ylabel("X")
plt.show()
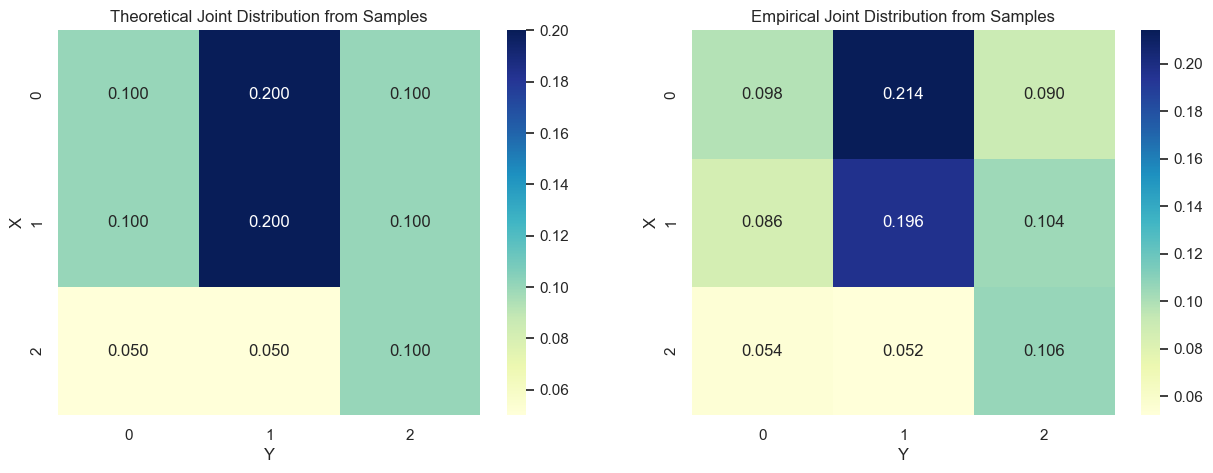
✅ 方法二:“边缘 + 条件分布采样法”(Marginal + Conditional Sampling)
这种方法在概率论、贝叶斯建模中非常常见,逻辑也更直观,尤其适用于结构化概率模型(如贝叶斯网)或条件概率信息清晰的场景。
采样一个二维离散随机变量 $(X, Y)$ 的基本思路是:
先从边缘分布 $P(X = x_i)$ 中采样一个 $x_i$, 然后根据这个 $x_i$,从条件分布 $P(Y = y_j \mid X = x_i)$ 中采样一个 $y_j$。
🧮 数学基础
联合概率可分解为:
$$ P(X = x_i, Y = y_j) = P(X = x_i) \cdot P(Y = y_j \mid X = x_i) $$所以我们可以按这个顺序采样!
✅ 举个具体例子
如果我们有联合分布表 $P(X,Y)$:
| y=0 | y=1 | y=2 | 合计 | |
|---|---|---|---|---|
| x=0 | 0.1 | 0.2 | 0.1 | 0.4 |
| x=1 | 0.1 | 0.2 | 0.1 | 0.4 |
| x=2 | 0.05 | 0.05 | 0.1 | 0.2 |
那么边缘分布(对Y求和):
$$ P(X = 0) = 0.4,\quad P(X = 1) = 0.4,\quad P(X = 2) = 0.2 $$以及条件分布 $P(Y = y_j \mid X = x_i)$(每一行归一化):
| y=0 | y=1 | y=2 | |
|---|---|---|---|
| x=0 | 0.25 | 0.5 | 0.25 |
| x=1 | 0.25 | 0.5 | 0.25 |
| x=2 | 0.25 | 0.25 | 0.5 |
import numpy as np
import random
def sample_2d_marginal_conditional(x_vals, y_vals, joint_probs):
# 计算边缘分布 P(X)
P_X = joint_probs.sum(axis=1) # shape (3,)
# 计算条件分布 P(Y | X)
P_Y_given_X = joint_probs / P_X[:, np.newaxis] # 每行除以对应 P(X)
# 1. 采样 X
x = random.choices(x_vals, weights=P_X)[0]
x_idx = x_vals.index(x)
# 2. 根据 P(Y|X=x) 采样 Y
y = random.choices(y_vals, weights=P_Y_given_X[x_idx])[0]
return (x, y)
import numpy as np
import matplotlib.pyplot as plt
import random
# 值域
x_vals = [0, 1, 2]
y_vals = [0, 1, 2]
# 联合概率矩阵
joint_probs = np.array([
[0.1, 0.2, 0.1],
[0.1, 0.2, 0.1],
[0.05, 0.05, 0.1]
])
N = 1000 # 采样次数
# 采样
samples = [sample_2d_marginal_conditional(x_vals, y_vals, joint_probs) for _ in range(N)]
x_sample, y_sample = zip(*samples)
# 可视化
import seaborn as sns
import pandas as pd
df = pd.DataFrame({'x': x_sample, 'y': y_sample})
pivot_table = pd.crosstab(df['x'], df['y'], normalize='all')
plt.figure(figsize=(15, 5))
plt.subplot(1, 2, 1)
sns.heatmap(joint_probs, annot=True, cmap="YlGnBu", fmt=".3f", xticklabels=y_vals, yticklabels=x_vals)
plt.title("Theoretical Joint Distribution from Marginal + Conditional Sampling")
plt.xlabel("Y")
plt.ylabel("X")
plt.subplot(1, 2, 2)
sns.heatmap(pivot_table, annot=True, cmap="YlGnBu", fmt=".3f", xticklabels=y_vals, yticklabels=x_vals)
plt.title("Empirical Joint Distribution from Marginal + Conditional Sampling")
plt.xlabel("Y")
plt.ylabel("X")
plt.show()
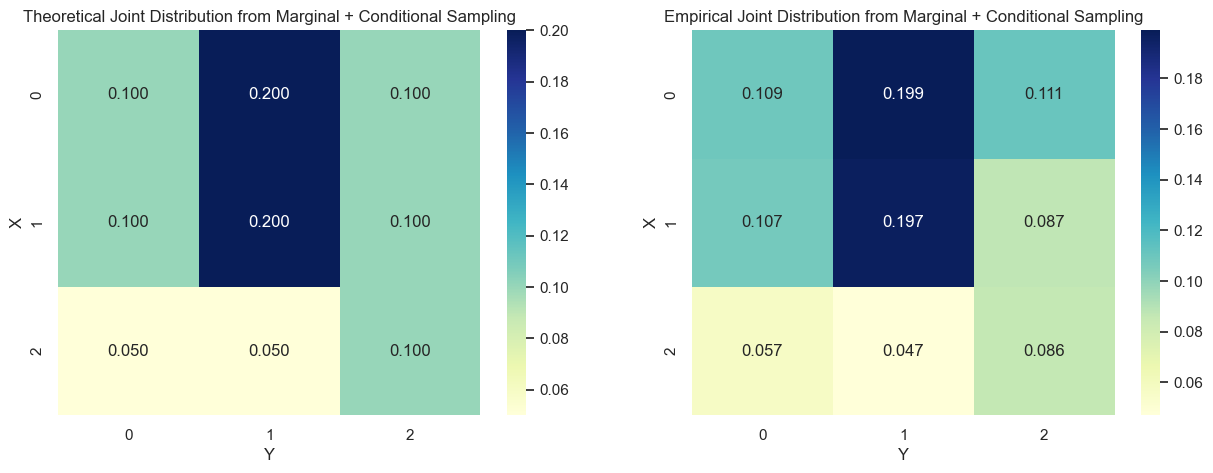
采样连续分布
格点采样器(Grid sampler)
格点采样器(Grid Sampler) 是一种基于二进制细分区间的递归采样方法,适用于近似从任意连续分布中采样,前提是我们可以计算任意区间的概率质量(积分)。
这个方法是用于高精度数值采样的构造性方法,特别适合:
- 分布没有封闭形式的逆CDF;
- 但我们可以计算其 CDF 或区间概率;
- 想从该分布中精确采样。
🔁 原理概述(以 [0,1] 区间为例)
目标:从某个连续概率密度函数 $f(x)$ 定义在 [0,1] 上采样。
📖 即使随机变量是定义在区间$[a,b]$上的,我们也可以通过线性变换将其转换到$[0,1]$。别忘了最后采样后,需要再做一次线性逆变换。
🧱 Step 1: 二进制划分区间
我们将区间 [0, 1] 分成 $2^N$ 个子区间,比如 $N = 3$ 时:
- 000 → $[0, \frac{1}{8})$
- 001 → $[\frac{1}{8}, \frac{2}{8})$
- …
- 111 → $[\frac{7}{8}, 1)$
这些可以对应为 二进制编码的区间编号。
🧠 Step 2: 利用条件概率构建一个样本点
我们不一次性计算所有 $2^N$ 个区间的概率,而是通过一个逐位决策过程来“走”进一个区间。
假设我们已经生成了前 $k$ 位: $b_1 b_2 \dots b_k$
那么这一部分所对应的区间是:
$$ I_k = \left[\frac{b}{2^k}, \frac{b+1}{2^k}\right), \quad b = \sum_{i=1}^k b_i \cdot 2^{k-i} $$下一位的值 $b_{k+1} \in \{0, 1\}$ 将进一步把 $I_k$ 分成左半或右半。
我们通过计算条件概率:
$$ \mathbb{P}(b_{k+1} = 0 \mid b_1 b_2 \dots b_k) = \frac{\mathbb{P}(x \in \text{left half of } I_k)}{\mathbb{P}(x \in I_k)} $$用这个条件概率掷一个硬币,决定下一位是 0 还是 1。重复 $N$ 次,就得到了一个近似采样结果:
$$ x = \sum_{i=1}^N b_i \cdot 2^{-i} \text{, where } b_i = \{0,1\} $$📌 总结流程
初始区间:[0,1]
每一步:
- 将当前区间分为左右两半
- 计算左半区间的概率 $p_L$
- 用 $p_L$ 进行伯努利采样,决定是走左边(bit=0)还是右边(bit=1)
迭代 N 次后,你就得到了一个二进制表达 $b_1b_2...b_N$
最终采样值:$x = \sum_{i=1}^N b_i \cdot 2^{-i}$,属于 [0,1] 上的某个子区间中
我们也可以一次构造所有区间的概率,将其转换为离散型,再使用离散型随机变量的采样方法(例如,反函数法)进行采样。
✅ 优点
- 适用于任意连续分布,只要能计算区间概率
- 无需求逆CDF或标准变换
- 可用于严格采样、测试、模拟复杂分布
⚠️ 注意事项
- 精度由 $N$ 控制:越大越精确,但计算代价越高;
- $\epsilon=log_2N$
- 必须能计算任意区间 $[a,b]$ 的概率:例如通过 CDF 函数;
- 和普通“先采 uniform 再求逆CDF”的方式不同,这是一种构造性的、位级别的采样方式。
import numpy as np
import matplotlib.pyplot as plt
# 设置参数
N = 6 # 树的深度(也即将 [0,1] 划分为 2^6 = 64 个区间)
def draw_path(ax, level, x0, x1, path=[]):
if level > N:
x_mid = (x0 + x1) / 2
y = -level
ax.plot(x_mid, y, 'ko') # 画叶子节点
bin_label = ''.join(str(b) for b in path)
ax.text(x_mid, y - 0.2, f"{bin_label}", ha='center', fontsize=8)
return
x_mid = (x0 + x1) / 2
y = -level
ax.plot(x_mid, y, 'ko') # 当前节点
# 左边
draw_path(ax, level + 1, x0, x_mid, path + [0])
ax.plot([x_mid, (x0 + x_mid) / 2], [y, y - 1], 'gray', lw=1)
# 右边
draw_path(ax, level + 1, x_mid, x1, path + [1])
ax.plot([x_mid, (x1 + x_mid) / 2], [y, y - 1], 'gray', lw=1)
# 画图
fig, ax = plt.subplots(figsize=(12, 6))
draw_path(ax, 0, 0.0, 1.0)
ax.set_ylim(-N - 1.5, 1)
ax.set_xlim(-0.05, 1.05)
ax.set_yticks([])
ax.set_xlabel("Interval on [0,1]")
ax.set_title("Grid Sampling: Binary Tree Partition (N=6)")
plt.grid(True, axis='x', linestyle='--', alpha=0.3)
plt.tight_layout()
plt.show()
🧪 举例:$\text{Beta}(2,5)$)
目标:我们已知一个连续分布(如 Beta 分布)的 PDF,可以计算任意区间的概率,但不能直接反解其 CDF。
Step 1: 将区间 [0, 1] 离散化为 2ⁿ 个子区间
比如 N = 10,将 [0,1] 均分为 1024 个小区间,每个区间宽度为 $\Delta x = \frac{1}{1024}$。
Step 2: 在每个子区间的中点处计算 PDF,并用这些近似概率来构造离散 PMF
我们用 beta.pdf 计算每个中点的概率密度,归一化得到一组近似的概率值 $p_i$,形成一个离散分布。
Step 3: 构建 CDF,然后使用一个 Uniform(0,1) 随机变量 u 来查找 u 落入哪个累积概率区间
我们用 np.searchsorted(cdf, u) 找到对应区间,再返回该区间中点作为采样值。
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import beta
# 设置 beta 分布参数
a, b = 2, 5 # Beta(2,5)
# 样本数量和分割深度
N = 10 # 将区间 [0,1] 分为 2^N = 1024 个小区间
num_samples = 10000
# 构建区间划分
intervals = np.linspace(0, 1, 2**N + 1)
midpoints = (intervals[:-1] + intervals[1:]) / 2 # 区间中点
probs = beta.pdf(midpoints, a, b) # 区间中点的概率密度
probs /= probs.sum() # 归一化成概率,从而获得一个新的离散分布
# 构建累积分布函数(CDF)
cdf = np.cumsum(probs) # 基于这个新的离散分布构建 CDF
# Grid sampling: 在每次采样时只用一个均匀随机数查找所属区间
uniform_samples = np.random.rand(num_samples)
samples = []
for u in uniform_samples:
idx = np.searchsorted(cdf, u)
# 选择该区间的中点作为采样值
samples.append(midpoints[idx])
# 可视化结果
x = np.linspace(0, 1, 500)
pdf = beta.pdf(x, a, b)
plt.figure(figsize=(10, 6))
plt.hist(samples, bins=50, density=True, alpha=0.6, label="Sampled Histogram")
plt.plot(x, pdf, 'r-', lw=2, label=f"Beta PDF a={a}, b={b}")
plt.title(f"Sampling Beta(2,5) using Grid Sampler (ε={1/(2**N):.4f})")
plt.xlabel("x")
plt.ylabel("Density")
plt.legend()
plt.grid(True)
plt.show()
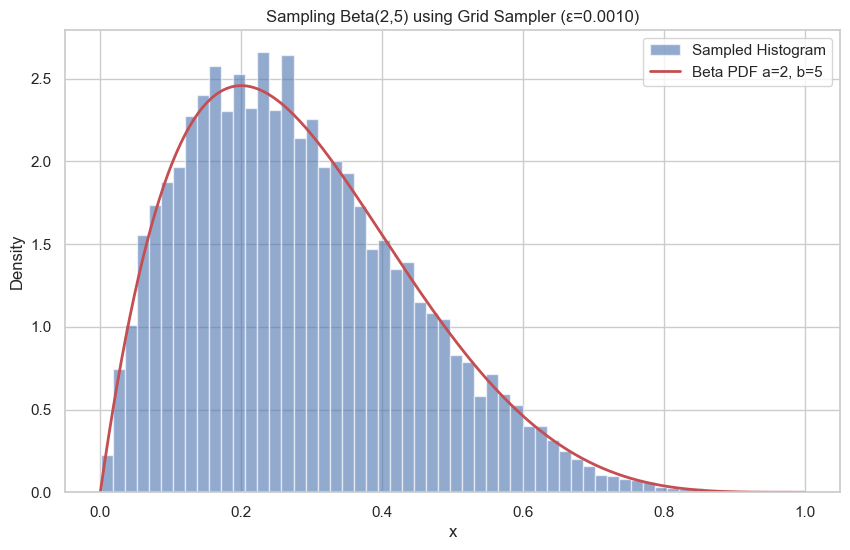
另一种实现:以 Beta(2,5) 分布为例
步骤:每次将区间一分为二,计算左边的概率,用它进行伯努利采样,最终拼出一个二进制小数。
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import beta
def grid_sampler(cdf_func, N):
"""
使用 Grid Sampler 从 [0,1] 上采样
:param cdf_func: 累积分布函数(例如 scipy.stats.beta(a,b).cdf)
:param N: 迭代次数(控制精度)
:return: 采样值 x ∈ [0,1]
"""
left, right = 0.0, 1.0
x_bits = []
for i in range(N):
mid = (left + right) / 2
p_left = (cdf_func(mid) - cdf_func(left)) / (cdf_func(right) - cdf_func(left)) # 归一化条件概率
b = np.random.rand() < p_left # 伯努利采样
x_bits.append(0 if b else 1)
# 更新区间
if b:
right = mid
else:
left = mid
# 将二进制结果转换为 [0,1] 上的小数值
x = sum(bit * (0.5 ** (i + 1)) for i, bit in enumerate(x_bits))
return x
# 设置参数
N = 10 # 精度控制
samples = [grid_sampler(beta(2, 5).cdf, N) for _ in range(10000)]
# 可视化
x = np.linspace(0, 1, 1000)
plt.figure(figsize=(10, 6))
plt.hist(samples, bins=50, density=True, alpha=0.6, label='Sampled via Grid Sampler')
plt.plot(x, beta.pdf(x, 2, 5), label='Beta(2,5) PDF', lw=2, color='red')
plt.title("Grid Sampling from Beta(2,5)")
plt.xlabel("x")
plt.ylabel("Density")
plt.legend()
plt.grid(True)
plt.show()
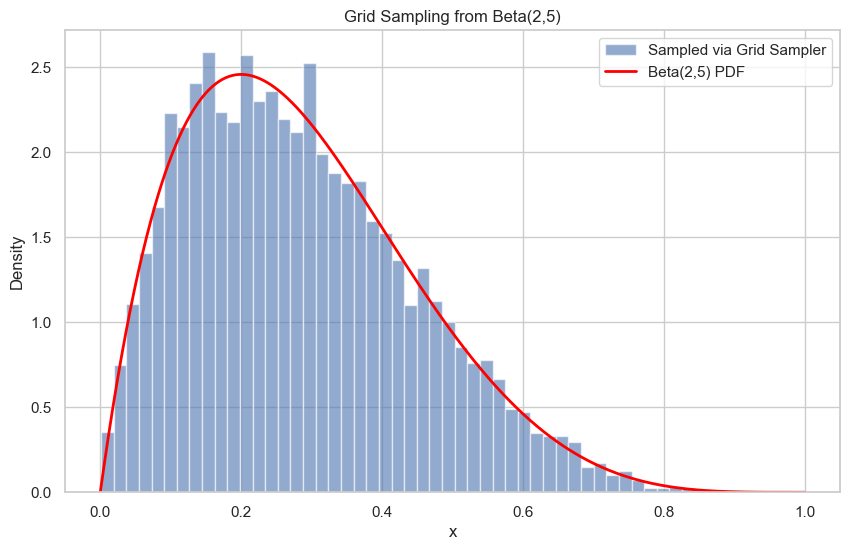
接受-拒绝采样(Acceptance-Rejection Sampling)
Acceptance-Rejection Sampling(接受-拒绝采样,简称 AR 采样)是一种非常重要且直观的 从复杂分布中采样的方法,特别适合当:
- ✅ 目标分布的 概率密度函数(PDF)可计算;
- 🚫 目标分布的 CDF 无法反解,不能直接使用反函数采样;
- ✅ 你有一个容易采样的辅助分布(proposal distribution)。
🧠 基本思想
如果你不能直接从复杂分布 $p(x)$ 采样,那就:
- 从一个容易采样的分布 $q(x)$ 采样;
- 然后“筛选”出落在目标分布 $p(x)$ 下的点!
📌 理论基础
从易采样的分布中筛选出服从 $p(x)$ 的样本
我们引入一个 proposal distribution $q(x)$,并要求存在常数 $M \geq 1$,使得:
$$ p(x) \leq M q(x),\quad \text{对所有 } x $$这样,$Mq(x)$ 就是 $p(x)$ 的“上界”。
✅ 理论基础一:联合分布与边缘分布
我们构造一个二维联合分布:
$$ (x, u) \sim \text{joint distribution}, \quad x \sim q(x),\quad u \sim \text{Uniform}(0, 1) $$然后定义一个二维区域:
$$ \mathcal{A} = \left\{ (x, u) : u \leq \frac{p(x)}{Mq(x)} \right\} $$那么我们在 $(x, u) \in \mathcal{A}$ 中保留的 $x$,其边缘分布就是 $p(x)$!
这点可从联合密度推导:
设联合密度为:
$$ f(x, u) = q(x) \cdot \mathbb{1}\left( 0 \leq u \leq \frac{p(x)}{Mq(x)} \right) $$那么对 $x$ 的边缘密度:
$$ f_{\text{accepted}}(x) = \int_0^{\frac{p(x)}{Mq(x)}} q(x) \, du = q(x)\cdot \frac{p(x)}{Mq(x)} = \frac{p(x)}{M} $$即每个保留下来的 $x$,分布比例为 $\propto p(x)$。说明接受的样本正比于 $p(x)$,即我们从 $p(x)$ 中采样了!
✅ 理论基础二:抽样一致性
虽然我们使用了“拒绝”的机制,但这其实就等价于对一个更大的分布进行条件采样:
我们从联合分布 $f(x, u) = q(x) \cdot \text{Unif}[0, Mq(x)]$ 中采样,然后保留符合条件的点。
保留下来的 $x$ 的分布是:
$$ p_{\text{accept}}(x) = \frac{p(x)}{M} \Rightarrow \text{Normalize后仍是 } p(x) $$🎲 算法步骤
对于每个样本:
- 从 proposal 分布 $q(x)$ 中采样一个候选点 $x \sim q(x)$
- 从均匀分布 $u \sim \text{Uniform}(0,1)$ 采一个辅助变量
- 接受 $x$ 当且仅当:
否则拒绝,重新采样。
📈 接受率和效率
接受率(acceptance rate)为:
$$ \text{Accept Rate} = \frac{1}{M} $$因此,选择尽可能接近 $f(x)$ 的 $M \cdot q(x)$ 很重要,这样可以减少浪费。
✅ 优点
- 不需要归一化常数 $Z$,可用于复杂分布(如未归一化的 posterior)
- 理论简单,直观
⚠️ 缺点
- 接受率可能非常低(尤其是高维情况下)
- 必须找到合适的 proposal 分布和合理的 M
🧠 总结一句话
接受-拒绝采样就是用一个容易采样的“外壳”包住目标分布,然后随机撒点,留下落在目标区域的那些点。
又见
import numpy as np
import plotly.graph_objects as go
from scipy.stats import beta
# 设置目标分布和 proposal
def f(x):
return beta.pdf(x, 2, 5)
def g(x):
return 1.0 # Uniform(0,1) 上的密度
# 设定常数 M
x_vals = np.linspace(0, 1, 500)
fx_vals = f(x_vals)
gx_vals = g(x_vals)
M = np.max(fx_vals) # M >= max(f(x)/g(x)),在这个例子中 g(x)=1,所以M=max(f(x))
# 开始采样
np.random.seed(42)
N = 500
x_samples = np.random.uniform(0, 1, N)
u_samples = np.random.uniform(0, 1, N)
accepted_x = []
accepted_y = []
rejected_x = []
rejected_y = []
for x, u in zip(x_samples, u_samples):
threshold = f(x) / M
if u < threshold:
accepted_x.append(x)
accepted_y.append(u * M) # 映射回 f(x) 的高度空间
else:
rejected_x.append(x)
rejected_y.append(u * M)
# 创建交互图
fig = go.Figure()
# 目标分布 f(x)
fig.add_trace(go.Scatter(x=x_vals, y=fx_vals, mode='lines', name='Target f(x)', line=dict(color='blue')))
# Proposal 分布 M * g(x)
fig.add_trace(go.Scatter(x=x_vals, y=[M * g(x) for x in x_vals], mode='lines', name='Mg(x)', line=dict(color='orange', dash='dash')))
# Accepted samples
fig.add_trace(go.Scatter(x=accepted_x, y=accepted_y, mode='markers', name='Accepted', marker=dict(color='green', size=6)))
# Rejected samples
fig.add_trace(go.Scatter(x=rejected_x, y=rejected_y, mode='markers', name='Rejected', marker=dict(color='red', size=4, opacity=0.5)))
fig.update_layout(title='Acceptance-Rejection Sampling with Joint Distribution View',
xaxis_title='x', yaxis_title='y',
height=500, width=800)
fig.show()
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation
# Target distribution: p(x) ∝ exp(-x^2 / 2) (standard normal, unnormalized)
def p(x):
return np.exp(-x**2 / 2)
# Proposal distribution: uniform over [-3, 3]
def q(x):
return np.full_like(x, 1 / 6)
# M such that p(x) <= M * q(x)
M = np.sqrt(2 * np.pi) / (1/6) # since max(p) = 1 when x=0
# Generate samples
np.random.seed(0)
n_samples = 1000
x_vals = np.random.uniform(-3, 3, n_samples)
u_vals = np.random.uniform(0, M * q(x_vals), n_samples)
# Create acceptance mask
accept = u_vals <= p(x_vals)
# Prepare animation frames
x_range = np.linspace(-3, 3, 500)
fig, ax = plt.subplots(figsize=(8, 5))
frames = []
for i in range(0, n_samples, 20):
ax.clear()
ax.plot(x_range, p(x_range), label='Target p(x)', color='orange')
ax.plot(x_range, M * q(x_range), label='M * q(x)', color='blue', linestyle='--')
ax.scatter(x_vals[:i], u_vals[:i], color='gray', s=10, alpha=0.3, label='Rejected')
ax.scatter(x_vals[:i][accept[:i]], u_vals[:i][accept[:i]], color='green', s=10, label='Accepted')
ax.set_xlim(-3, 3)
ax.set_ylim(0, M * 1.1 * np.max(q(x_range)))
ax.set_title("Acceptance-Rejection Sampling")
ax.legend(loc='upper right')
ax.grid(True)
# Capture the current frame
frame = plt.gcf().canvas.copy_from_bbox(ax.bbox)
frames.append([plt.scatter([], [])]) # dummy to hold frames
# Re-render using FuncAnimation
def update(i):
ax.clear()
ax.plot(x_range, p(x_range), label='Target p(x)', color='orange')
ax.plot(x_range, M * q(x_range), label=f'M * q(x) (M={M:.2f})', color='blue', linestyle='--')
ax.scatter(x_vals[:i], u_vals[:i], color='gray', s=10, alpha=0.3, label='Rejected')
ax.scatter(x_vals[:i][accept[:i]], u_vals[:i][accept[:i]], color='green', s=10, label='Accepted')
ax.set_xlim(-3, 3)
ax.set_ylim(0, M * 1.1 * np.max(q(x_range)))
ax.set_title(f"Acceptance-Rejection Sampling (Step {i})")
ax.legend(loc='upper right')
ax.grid(True)
ani = animation.FuncAnimation(fig, update, frames=range(0, n_samples, 20), interval=100)
# Save as GIF
from matplotlib.animation import PillowWriter
ani.save("acceptance_rejection_sampling.gif", writer=PillowWriter(fps=10))
plt.close(fig)
from IPython.display import Image
Image(filename="acceptance_rejection_sampling.gif")
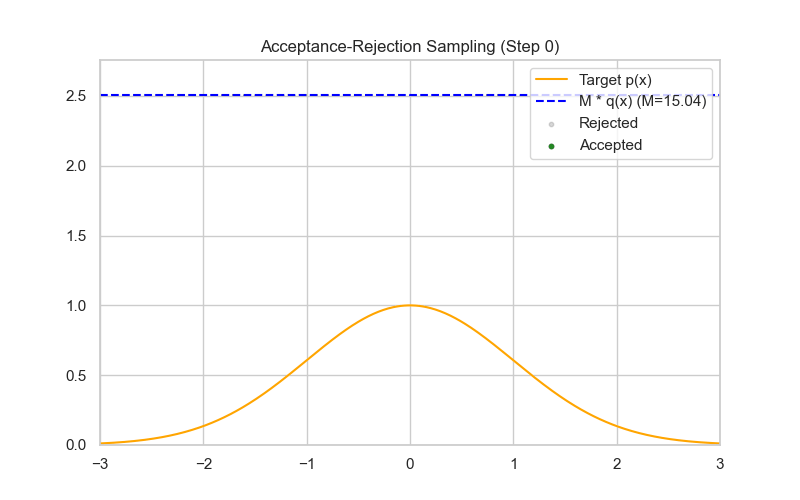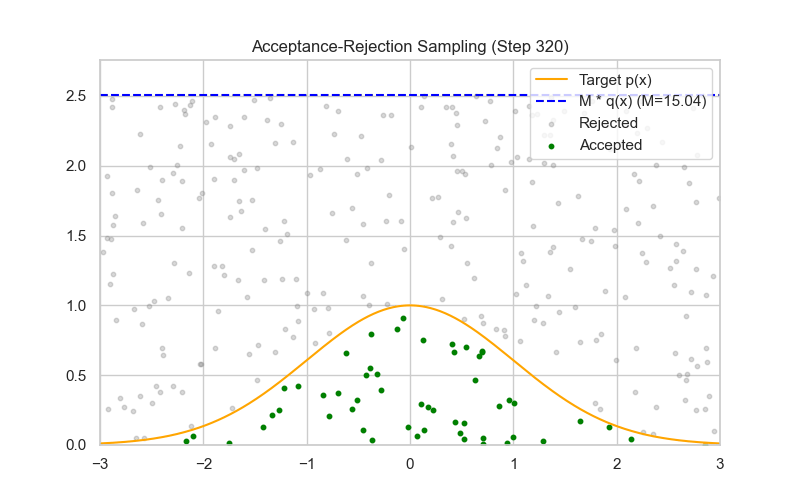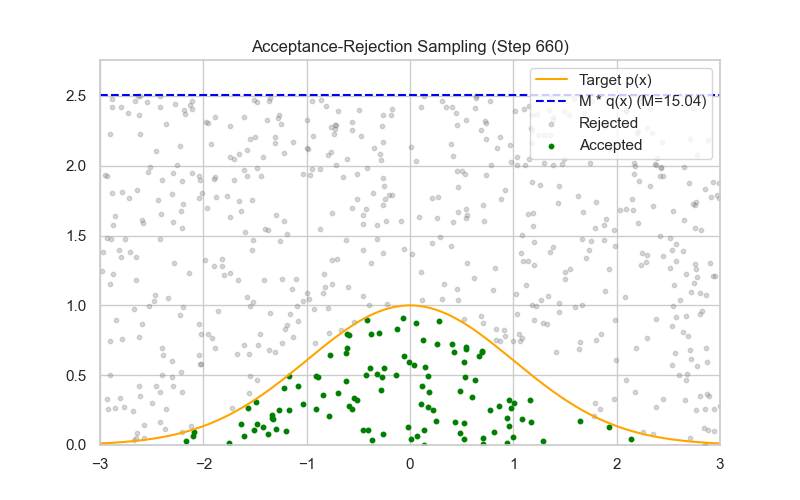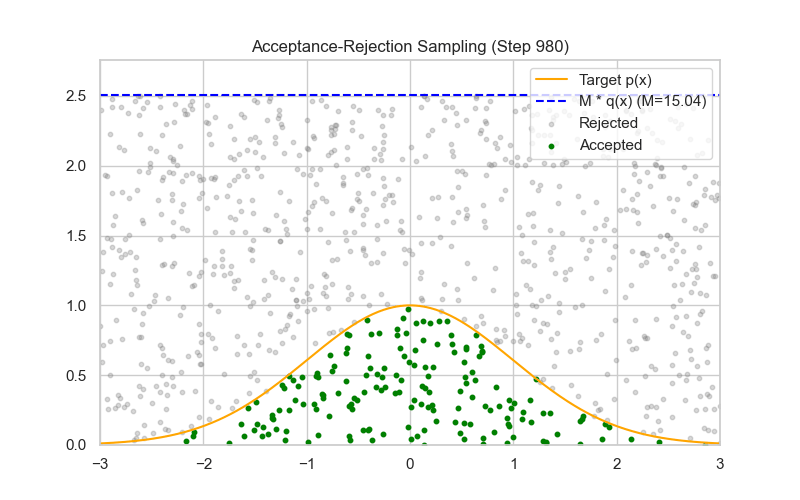
附录
从已知二维随机变量 (X, Y) 中采样其极坐标变换后的随机变量
从已知二维随机变量 $(X, Y)$ 中采样其极坐标变换后的随机变量 $(R^2, \alpha)$,其中:
- $r^2 = x^2 + y^2$,范围为 $(0, \infty)$
- $\alpha = \arctan(y/x)$,范围为 $(0, 2\pi)$
🧮 1. 变量变换和雅可比(Jacobian)推导
我们定义新的变量:
$$ \begin{cases} u(x,y) = r^2 = x^2 + y^2 \\ v(x,y) = \alpha = \arctan\left(\frac{y}{x}\right) \end{cases} \Rightarrow \begin{cases} x = \sqrt{u} \cos v \\ y = \sqrt{u} \sin v \end{cases} $$计算 Jacobian:
我们计算从 $(u, v)$ 到 $(x, y)$ 的雅可比行列式:
$$ J = \begin{vmatrix} \frac{\partial x}{\partial u} & \frac{\partial x}{\partial v} \\ \frac{\partial y}{\partial u} & \frac{\partial y}{\partial v} \end{vmatrix} $$先求导:
- $\frac{\partial x}{\partial u} = \frac{1}{2\sqrt{u}} \cos v$
- $\frac{\partial x}{\partial v} = -\sqrt{u} \sin v$
- $\frac{\partial y}{\partial u} = \frac{1}{2\sqrt{u}} \sin v$
- $\frac{\partial y}{\partial v} = \sqrt{u} \cos v$
代入 Jacobian:
$$ J = \left| \begin{matrix} \frac{1}{2\sqrt{u}} \cos v & -\sqrt{u} \sin v \\ \frac{1}{2\sqrt{u}} \sin v & \sqrt{u} \cos v \end{matrix} \right| = \frac{1}{2\sqrt{u}} \cos v \cdot \sqrt{u} \cos v + \sqrt{u} \sin v \cdot \frac{1}{2\sqrt{u}} \sin v = \frac{1}{2}(\cos^2 v + \sin^2 v) = \frac{1}{2} $$所以雅可比行列式为:
$$ |J| = \frac{1}{2} $$🧪 2. 密度函数变换公式
若 $(X, Y)$ 的联合密度为 $f_{X,Y}(x,y)$,则变换后:
$$ f_{R^2, \alpha}(u, v) = f_{X,Y}(x(u,v), y(u,v)) \cdot \left|J\right|^{-1} = 2 f_{X,Y}(\sqrt{u} \cos v, \sqrt{u} \sin v) $$import numpy as np
import matplotlib.pyplot as plt
# 构建 (x, y) 网格
x = np.linspace(-2, 2, 400)
y = np.linspace(-2, 2, 400)
X, Y = np.meshgrid(x, y)
# 原始坐标系下的函数:r^2 = x^2 + y^2, alpha = arctan2(y, x)
R2 = X**2 + Y**2
Alpha = np.arctan2(Y, X)
# 绘制 r^2 等高线
fig, ax = plt.subplots(1, 2, figsize=(12, 5))
r2_levels = [0.5, 1.0, 2.0, 3.0]
alpha_levels = [-np.pi, -np.pi/2, 0, np.pi/2, np.pi]
cont1 = ax[0].contour(X, Y, R2, levels=r2_levels, cmap="Blues")
ax[0].clabel(cont1, fmt="r²=%.1f")
ax[0].set_title("Contours of $r^2 = x^2 + y^2$")
ax[0].set_xlabel("x")
ax[0].set_ylabel("y")
ax[0].axis("equal")
ax[0].grid(True)
# 绘制 alpha 等高线
cont2 = ax[1].contour(X, Y, Alpha, levels=alpha_levels, cmap="coolwarm")
ax[1].clabel(cont2, fmt="α=%.2f")
ax[1].set_title(r"Contours of $\alpha = \arctan2(y, x)$")
ax[1].set_xlabel("x")
ax[1].set_ylabel("y")
ax[1].axis("equal")
ax[1].grid(True)
plt.tight_layout()
plt.show()
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
from IPython.display import HTML
# 创建网格
x = np.linspace(-1, 1, 20)
y = np.linspace(-1, 1, 20)
X, Y = np.meshgrid(x, y)
points = np.stack([X.ravel(), Y.ravel()], axis=1)
# 非线性变换(模拟 Jacobian 拉伸效果)
def transform(points, alpha):
x, y = points[:, 0], points[:, 1]
r = np.sqrt(x**2 + y**2)
theta = np.arctan2(y, x)
r_new = r + alpha * np.sin(3 * theta) # 添加扰动模拟形变
x_new = r_new * np.cos(theta)
y_new = r_new * np.sin(theta)
return np.stack([x_new, y_new], axis=1)
# 初始化画布
fig, ax = plt.subplots(figsize=(6, 6))
scat = ax.scatter(points[:, 0], points[:, 1], s=10)
ax.set_xlim(-2, 2)
ax.set_ylim(-2, 2)
ax.set_aspect('equal')
ax.set_title("Jacobian Deformation Demo")
# 帧更新函数
def update(frame):
alpha = 0.3 * np.sin(frame / 10)
new_points = transform(points, alpha)
scat.set_offsets(new_points)
return scat,
# 动画
ani = FuncAnimation(fig, update, frames=100, interval=100, blit=True)
# 保存为 GIF(可选)
from matplotlib.animation import PillowWriter
ani.save("jacobian_area_deformation.gif", writer=PillowWriter(fps=10))
plt.close(fig)
from IPython.display import Image
Image(filename="jacobian_area_deformation.gif")
#HTML(ani.to_jshtml())
🎯 3. 采样方案设计
✅ 一般步骤:
从已知联合分布 $f_{X,Y}(x,y)$ 中采样一组 $(x,y)$
将其转换为极坐标形式:
$$ r^2 = x^2 + y^2, \quad \alpha = \arctan2(y, x) $$得到样本 $(r^2, \alpha)$
✅ 反过来:若你有 $f_{R^2, \alpha}(r^2, \alpha)$,如何采样?
方法一(反函数采样):若 $r^2$ 和 $\alpha$ 可独立分布表示,直接分别采样再组合。
方法二(接受-拒绝采样):设计 proposal distribution,比如:
- $r^2 \sim \text{Gamma}(k, \theta)$
- $\alpha \sim \text{Uniform}(0, 2\pi)$
然后利用目标密度 $f_{R^2, \alpha}$ 与 proposal 做比值,使用 rejection rule 接受或拒绝。