概率的三种解释
🔵 1. 频率学派解释(Frequentist Interpretation)
🌱 核心思想:
概率是长期频率的极限,是指在无限重复的独立实验中,某个事件发生的比例。
概率就是长期重复中事件发生的频率。
📌 数学表达:
如果我们独立重复实验 $n$ 次,事件 $A$ 发生了 $n_A$ 次,那么:
$$ P(A) = \lim_{n \to \infty} \frac{n_A}{n} $$🧠 关键特征:
- 概率是客观存在,与观察者无关。
- 概率只适用于可重复实验(如掷硬币、抽球、做测量)。
- 不适用于一次性事件(例如预测明年是否会发生战争)。
🎯 应用示例:
- 抛硬币、掷骰子、抽样调查
- 参数估计:最大似然估计(MLE)
- 假设检验(p-value、置信区间等)
⚠️ 缺点:
- 对一次性事件无能为力(无法定义频率)
- 不能表达主观不确定性(如“我相信这幅画是毕加索的真迹”的概率)
# 重新执行所需库导入和动画绘制代码
import matplotlib.pyplot as plt
import numpy as np
import matplotlib.animation as animation
# 设置随机种子以保证可重复性
np.random.seed(42)
# 模拟抛硬币 n 次(0 表示反面,1 表示正面)
n_trials = 2000
outcomes = np.random.choice([0, 1], size=n_trials)
cumulative_heads = np.cumsum(outcomes)
frequencies = cumulative_heads / np.arange(1, n_trials + 1)
# 创建动画图形
fig, ax = plt.subplots()
line, = ax.plot([], [], lw=2)
ax.set_xlim(0, n_trials)
ax.set_ylim(0, 1)
ax.axhline(0.5, color='red', linestyle='--', label='True Probability = 0.5')
ax.set_xlabel('Number of Trials')
ax.set_ylabel('Frequency of Heads')
ax.set_title('Frequency Converges to Probability')
ax.legend()
def init():
line.set_data([], [])
return line,
def update(frame):
x = np.arange(1, frame + 1)
y = frequencies[:frame]
line.set_data(x, y)
return line,
ani = animation.FuncAnimation(fig, update, frames=np.arange(10, n_trials, 10),
init_func=init, blit=True)
# Save as GIF
from matplotlib.animation import PillowWriter
ani.save("frequency_converges_to_probability.gif", writer=PillowWriter(fps=10))
plt.close(fig)
from IPython.display import Image
Image(filename="frequency_converges_to_probability.gif")
# 随着实验次数增加,频率逐渐收敛于真实概率(红线)
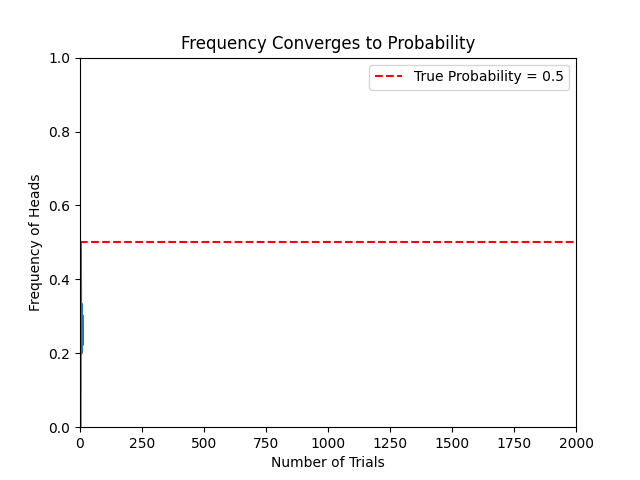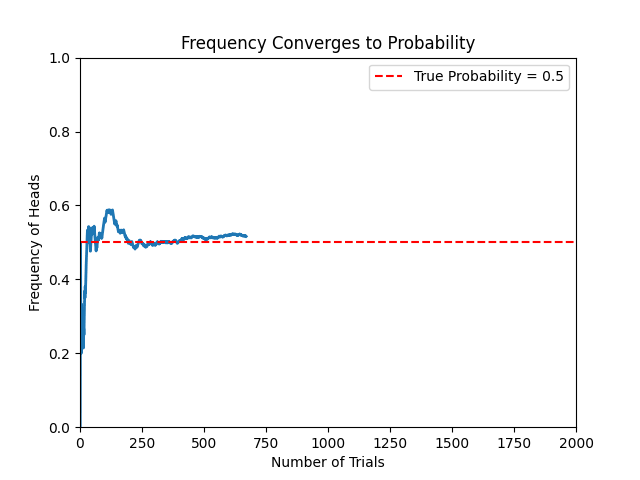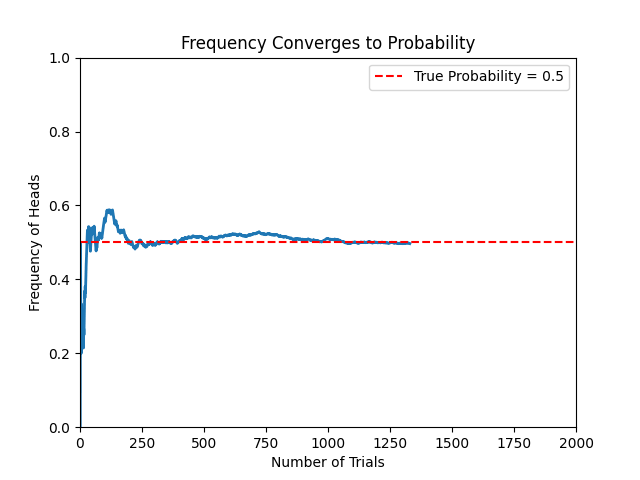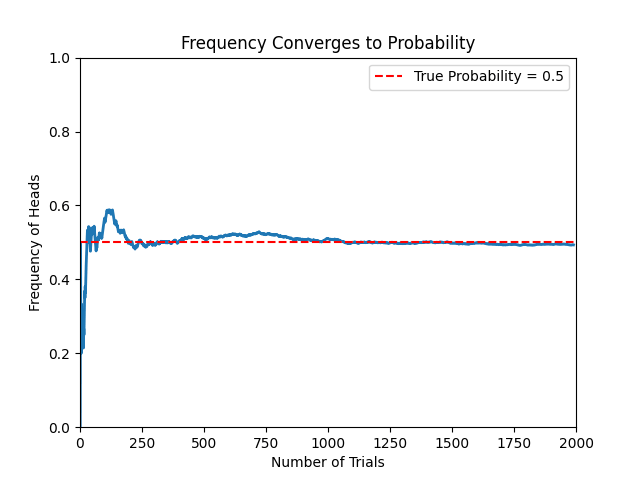
🔴 2. 贝叶斯学派解释(Bayesian Interpretation)
🌱 核心思想:
概率是主观信念的量化,用于表达观察者对某个事件发生的“相信程度”。
概率是你对事件不确定性的主观度量。
📌 数学表达:
根据贝叶斯公式(Bayes’ Theorem),即 后验概率 = 标准似然度*先验概率,有:
其中:
- $\theta$:一个随机变量
- $P(\theta)$:先验(你原本的信念)
- $P(\text{data}|\theta)$:似然(数据的生成机制)
- $P(\theta|\text{data})$:后验(观察数据后更新的信念)
- $\frac{P(\text{data}|\theta)}{P(\text{data})}$:标准似然度(standardised likelihood)
从条件概率推导贝叶斯理论
贝叶斯理论可以表示为 $P(A|B) = \frac{P(A)P(B|A)}{P(B)}$。根据条件概率的定义,我们有
$$ P(A|B) = \frac{P(AB)}{P(B)} \rightarrow P(AB) = P(A|B)P(B)\\ P(B|A) = \frac{P(AB)}{P(A)} \rightarrow P(AB) = P(B|A)P(A) $$因此,
$$ P(A|B)P(B) = P(B|A)P(A) \rightarrow P(A|B) = \frac{P(A)P(B|A)}{P(B)} $$🧠 关键特征:
- 概率是主观的,依赖于观察者的背景知识
- 可以为任何事件赋予概率,包括一次性事件
- 核心机制是更新信念:prior → posterior
🎯 应用示例:
- 医学诊断(医生对病人患病概率的判断)
- 人工智能中的贝叶斯网络、决策系统
- 参数估计:贝叶斯推断(MCMC 方法)
⚠️ 缺点:
- 先验的选择带有主观性
- 计算可能较复杂(尤其后验分布难以解析)
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
from scipy.stats import beta
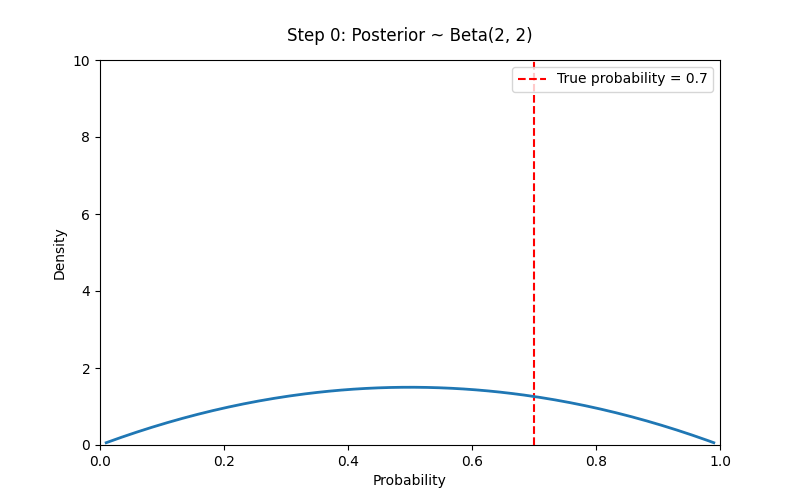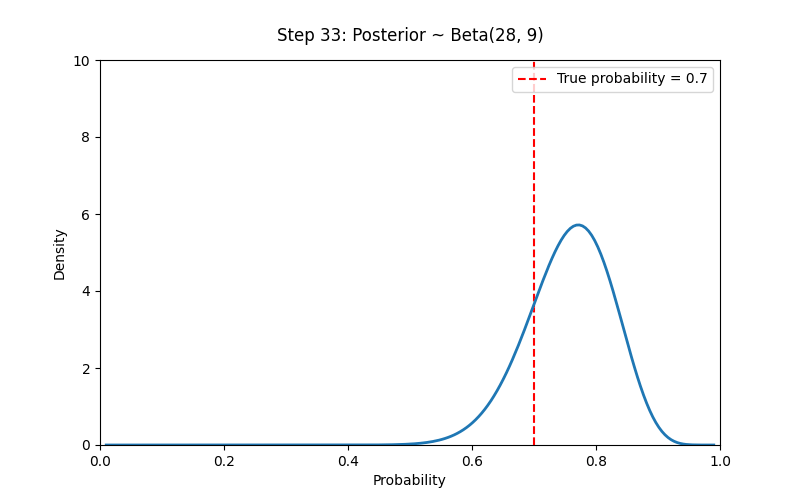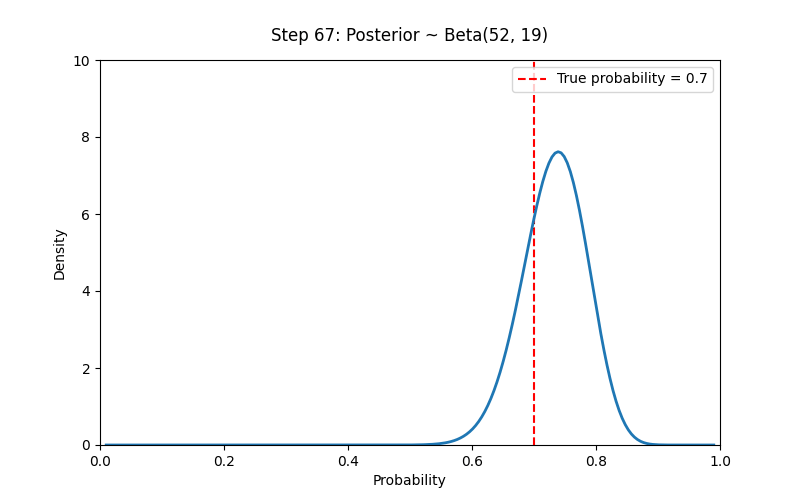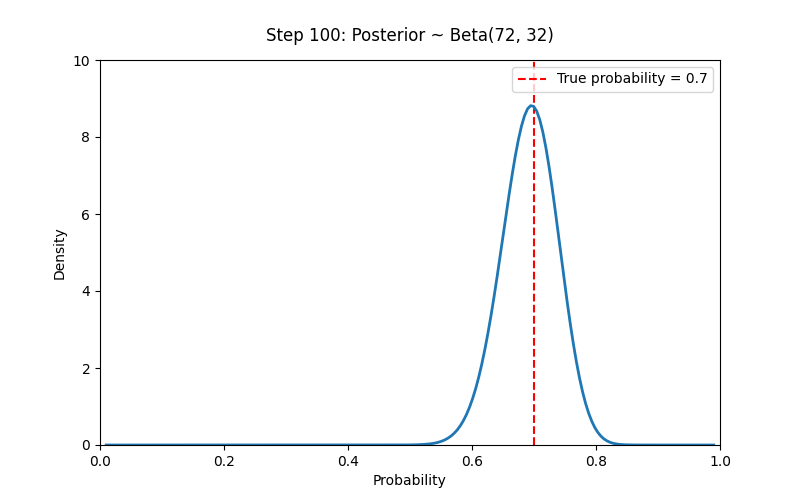
# 设置先验参数
a_prior, b_prior = 2, 2 # Prior ~ Beta(2,2)
# 模拟观测数据(例如抛硬币)
np.random.seed(42)
true_p = 0.7
N_trials = 100
data = np.random.binomial(1, true_p, size=N_trials) # 1 表示正面
# 创建 Beta 分布动画:从先验到后验
fig, ax = plt.subplots(figsize=(8, 5))
ax.vlines(true_p, 0, 10, colors='red', linestyles='--', label=f'True probability = {true_p}')
x = np.linspace(0.01, 0.99, 200)
line, = ax.plot([], [], lw=2)
title = ax.text(0.5, 1.05, "", ha="center", transform=ax.transAxes, fontsize=12)
ax.legend()
def init():
ax.set_xlim(0, 1)
ax.set_ylim(0, 10)
ax.set_xlabel("Probability")
ax.set_ylabel("Density")
line.set_data([], [])
return line, title
def update(i):
if i == 0:
a_post, b_post = a_prior, b_prior
else:
a_post = a_prior + np.sum(data[:i])
b_post = b_prior + i - np.sum(data[:i])
y = beta.pdf(x, a_post, b_post)
line.set_data(x, y)
title.set_text(f"Step {i}: Posterior ~ Beta({a_post}, {b_post})")
return line, title
ani = FuncAnimation(fig, update, frames=N_trials + 1, init_func=init,
blit=True, interval=300)
# Save as GIF
from matplotlib.animation import PillowWriter
ani.save("probability_Bayesian_update_prior_to_posterior.gif", writer=PillowWriter(fps=10))
plt.close(fig)
from IPython.display import Image
Image(filename="probability_Bayesian_update_prior_to_posterior.gif")
# 贝叶斯学派的核心思想:我们对概率的认识随着证据逐步更新,而概率本身反映了我们的主观不确定性。
⚫️ 3. 公理化定义(Kolmogorov Axiomatic Approach)
🌱 核心思想:
概率是一种满足特定公理体系的抽象数学结构,脱离主观或经验解释。
概率是定义在样本空间上的数学测度。
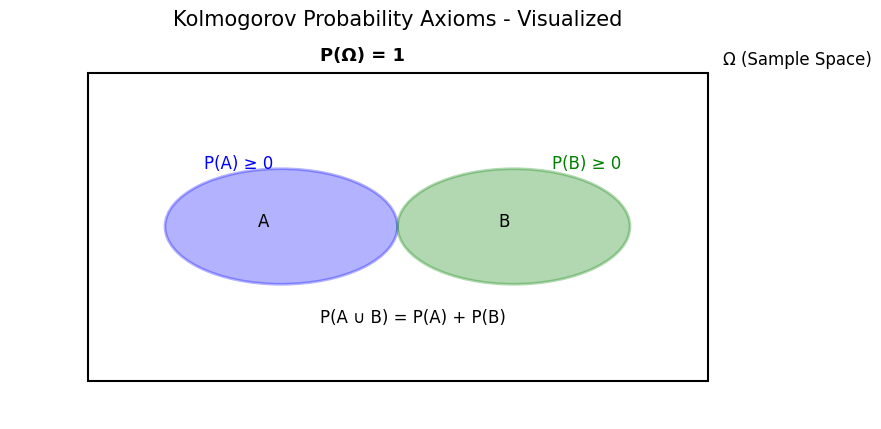
📌 三大公理(Kolmogorov 公理):
设 $\Omega$ 是样本空间,$\mathcal{F}$ 是事件集合(σ-代数),$P$ 是概率函数,则满足:
非负性(Non-negativity):
$$ \forall A \subseteq \Omega, \quad P(A) \geq 0 $$规范性(Normalization):
$$ P(\Omega) = 1 $$可列可加性(Countable Additivity): 对任意两两不相交事件 $A_1, A_2, A_3, \ldots$:
$$ P\left( \bigcup_{i=1}^{\infty} A_i \right) = \sum_{i=1}^{\infty} P(A_i) $$
样本空间 $\Omega$
一个非空集合,其中的元素称为结果或者样本输出,记作 $\omega$。
事件集合 $\mathcal{F}$
样本空间的一个子集我们称之为一个事件。而事件集合,顾名思义就是事件的一个集合,它是样本空间 $\Omega$ 幂集 $2^\Omega$ 的一个非空集合。而我们说 $\mathcal{F}$ 是一个σ-代数,则表示 $\mathcal{F}$ 必须满足下面性质:
- $\mathcal{F}$ 包含全集,即 $\Omega {\in }{\mathcal {F}}$
- $A \in \mathcal{F} \rightarrow {\bar {A}} \in \mathcal{F}$
- $A_{n}{\in }{\mathcal {F}}, n=1,2,... \rightarrow \bigcup _{n=1}^{\infty }A_{n}{\in }{\mathcal {F}}$
注:要求事件集合是 σ-代数是为了保证“补集、可列并”运算结果仍然是事件,从而 $P$ 在这些运算下有意义。
概率函数 $P:{\mathcal {F}}{\to }\mathbb {R}$
🧠 关键特征:
- 摆脱了频率与主观性,完全建立在集合论和测度论的基础上
- 是现代概率论与随机过程的基础
- 能兼容频率学派和贝叶斯解释
🎯 应用示例:
- 概率空间、期望、随机变量的严格定义
- 支撑高等概率论与统计学(如马尔可夫过程、布朗运动)
- 计算机随机模拟中的抽象建模
⚠️ 缺点:
- 不解释“概率到底是什么”,只描述“概率应该满足什么规则”
- 对初学者不够直观
import matplotlib.pyplot as plt
from matplotlib_venn import venn2, venn3
import matplotlib.patches as patches
# 设置画布
fig, ax = plt.subplots(figsize=(10, 5))
# 显示一个全集 Ω
omega = patches.Rectangle((0.1, 0.1), 0.8, 0.8, linewidth=1.5, edgecolor='black', facecolor='none')
ax.add_patch(omega)
ax.text(0.92, 0.92, 'Ω (Sample Space)', fontsize=12)
# 两个事件 A 和 B(不相交)
circle_A = patches.Circle((0.35, 0.5), 0.15, linewidth=2, edgecolor='blue', facecolor='blue', alpha=0.3)
circle_B = patches.Circle((0.65, 0.5), 0.15, linewidth=2, edgecolor='green', facecolor='green', alpha=0.3)
ax.add_patch(circle_A)
ax.add_patch(circle_B)
ax.text(0.32, 0.5, 'A', fontsize=12)
ax.text(0.63, 0.5, 'B', fontsize=12)
# 标注概率
ax.text(0.25, 0.65, 'P(A) ≥ 0', fontsize=12, color='blue')
ax.text(0.7, 0.65, 'P(B) ≥ 0', fontsize=12, color='green')
ax.text(0.4, 0.25, 'P(A ∪ B) = P(A) + P(B)', fontsize=12, color='black')
# 整个空间的概率为1
ax.text(0.4, 0.93, 'P(Ω) = 1', fontsize=13, weight='bold')
# 去掉坐标轴
ax.axis('off')
plt.title("Kolmogorov Probability Axioms - Visualized", fontsize=15)
plt.show()
📌 总结
| 解释方式 | 概率含义 | 适用场景 | 代表人物/思想 |
|---|---|---|---|
| 频率学派 | 长期频率 | 可重复实验 | Von Mises, Fisher |
| 贝叶斯学派 | 主观信念 | 单次事件、认知决策 | Thomas Bayes, Laplace |
| 公理化定义 | 抽象测度 | 理论建模、严谨数学推导 | Andrey Kolmogorov |
- 频率解释:概率是长期实验中的频率 → 客观经验主义。
- 贝叶斯解释:概率是主观信念的量化 → 信念更新机制。
- 公理定义:概率是满足一定规则的数学函数 → 抽象结构主义。
事件与样本空间
样本空间(Sample Space)
(直观)定义:样本空间记作 $\Omega$,是一次随机试验所有可能结果的集合。
离散样本空间:结果可数(或有限)。例如掷一个六面骰子:
$$ \Omega=\{1,2,3,4,5,6\}. $$再比如投三次硬币,所有可能序列共有 $2^3=8$ 个:$\{HHH, HHT,\dots, TTT\}$。
连续样本空间:结果是连续取值的区间或实数集合,不能一一列举。比如测量某人的身高(米):
$$ \Omega = [0, +\infty) \quad\text{或更常用 } \Omega=\mathbb{R}. $$或者把位置视为 $[0,1]$ 上的一个实数(均匀分布例子)。
要点:样本空间就是“我们列出所有可能发生的基本情况”的地方。离散可以数出来、连续不能数出来。
事件(Event)
(直观)定义:事件就是样本空间的一个子集 —— 表示“满足某个条件”的所有样本点的集合。事件可以包含一个结果(原子事件)或许多结果。
常见事件类型:
- 基本事件(elementary event):只包含一个结果。例如掷骰子得到 3:$\{3\}$。
- 复合事件(compound event):包含多个结果,例如“掷出偶数”$= \{2,4,6\}$。
- 必然事件(certain event):等于整个样本空间 $\Omega$(概率为 1)。
- 不可能事件(impossible / null event):空集 $\varnothing$(概率为 0)。
事件的运算
给定事件 $A,B$,可以做
- 并($A\cup B$:发生 A 或 B)
- 交($A\cap B$:同时发生)
- 补($A^c$:不发生 A)
举例说明(掷骰子):
- $A$:“掷出偶数” $=\{2,4,6\}$。
- $B$:“掷出大于 3” $=\{4,5,6\}$。
- 则 $A\cap B=\{4,6\}$,$A\cup B=\{2,4,5,6\}$。
如何把“概率”分配到事件上
对 离散:给每个基本结果 $\omega \in \Omega$ 赋一个概率 $P(\{\omega\})$,满足它们相加为 1。事件 $A$ 的概率就是其包含的基本概率之和:
$$ P(A)=\sum_{\omega\in A}P(\{\omega\}). $$对 连续:不能直接给单点概率(通常为 0),而是使用概率密度函数(PDF) $f(x)$,事件 $A$ 的概率是对 $A$ 积分:
$$ P(A)=\int_A f(x)\,dx. $$
三个常见示例
A. 掷骰子(离散、简单)
- 样本空间 $\Omega=\{1,2,3,4,5,6\}$(若均匀,每面概率 $1/6$)。
- 事件:$A=\{\text{偶数}\}=\{2,4,6\}$
- 则事件 $A$ 的概率是:$P(A)=3\times\frac{1}{6}=\frac{1}{2}$。
B. 天气预测(有限离散,但带概率)
- 样本空间可设 $\Omega=\{\text{晴},\text{阴},\text{雨}\}$。
- 根据历史我们可能估计 $P(\text{晴})=0.6,\ P(\text{阴})=0.3,\ P(\text{雨})=0.1$。
- 事件:明天“不下雨” $= \{\text{晴},\text{阴}\}$,概率 $0.9$。
注:天气例子展示“概率是基于历史频率或模型估计”的情形(频率或贝叶斯都可以给出解释)。
C. 图像分类(高维、不可枚举离散)
- 抽象地说:样本空间是“所有可能的数字图片集合”,记为 $ \Omega = \{\text{所有 } H\times W\times 3 \text{ 像素矩阵}\}$。
- 事件例如“图像包含猫”是 $A\subset\Omega$:所有被标注为猫的图像集合。你无法列举或逐点赋值,但可以用模型(分类器)或数据集近似 $P(A)$。
- 这展示:事件不必是“可枚举的集合”,它可以是非常大的集合(需要用概率模型、密度估计或经验频率来处理)。
概率的基本性质
由 Kolmogorov 公理导出的基本推论
命题 1:空事件概率为 0
$\displaystyle P(\varnothing)=0.$
证明:因为 $\Omega$ 与空集互补且 $\Omega=\varnothing\cup\Omega$,由可列可加性(取序列 $A_1=\Omega,A_2=\varnothing,A_3=\varnothing,\dots$),或更简单地注意到 $\Omega$ 与 $\varnothing$ 不相交并 $P(\Omega)=1$。而更标准的证明方法是利用可加性:
$$ P(\Omega)=P(\varnothing\cup\Omega)=P(\varnothing)+P(\Omega)\Rightarrow P(\varnothing)=0. $$(用非负性可得唯一解)
命题 2:单调性(Monotonicity)
若 $A\subseteq B$(两者均为事件),则 $P(A)\le P(B)$。
证明:写 $B=A\cup (B\setminus A)$,且 $A$ 与 $B\setminus A$ 不相交。由可加性与非负性:
$$ P(B)=P(A)+P(B\setminus A)\ge P(A). $$命题 3:补事件概率规则
$\displaystyle P(A^c)=1-P(A)$。
证明:由 $A\cup A^c=\Omega$ 且 $A\cap A^c=\varnothing$,应用可加性:
$$ P(\Omega)=P(A)+P(A^c)=1\Rightarrow P(A^c)=1-P(A). $$命题 4:两个事件的加法公式(包含交集修正项)
$$ P(A\cup B)=P(A)+P(B)-P(A\cap B). $$证明(分区法):把 $A$ 与 $B$ 分为不相交三块:
$$ A=(A\setminus B)\cup(A\cap B),\quad B=(B\setminus A)\cup(A\cap B). $$并且
$$ A\cup B=(A\setminus B)\cup(A\cap B)\cup(B\setminus A) $$三部分两两不交,应用可加性可得:
$$ P(A) = P(A\setminus B) + P(A\cap B) \rightarrow P(A\setminus B) = P(A) - P(A\cap B) \\ P(B) = P(B\setminus A) + P(A\cap B) \rightarrow P(B\setminus A) = P(B) - P(A\cap B) \\ P(A\cup B) =P(A\setminus B) + P(A\cap B) + (B\setminus A) = P(A) - P(A\cap B) + P(A\cap B) + P(B) - P(A\cap B) = P(A) + P(B) - P(A\cap B) $$由此得证。
命题 5:容斥原理(两个与三个事件的情况)
- 两个事件:同上(加法公式)。
- 三个事件:
证明:把三集按互不相交的最小原子(8 个原子)分解,或从两集合的公式递推和减去多次计数得来(标准的容斥推导)。
命题 6:有限可加性(从可列可加性退化而来)
若 $A_1,\dots,A_n$ 两两不交,则
$$ P\Big(\bigcup_{i=1}^n A_i\Big)=\sum_{i=1}^n P(A_i). $$这是公理的直接特例(只取有限项即可)。
命题 7:并集的上界(Boole 不等式 / Union bound)
对任意事件序列(不必互斥) $A_1,A_2,\dots$,有
$$ P\Big(\bigcup_{i=1}^\infty A_i\Big)\le \sum_{i=1}^\infty P(A_i). $$证明要点:把并集拆成互不相交的子集或直接用单调性与可列可加性证明(可把并集写成不相交的并列或利用对序列 $B_1=A_1, B_2=A_2\setminus A_1, \dots$),从而求得上界。
命题 8:连续性(从上与下)
- 从上连续性:若 $A_1\supseteq A_2\supseteq\cdots$ 且交集 $\bigcap_n A_n=\varnothing$,则 $P(A_n)\downarrow 0$(趋于 0)。
- 从下连续性:若 $A_1\subseteq A_2\subseteq\cdots$ 且并集 $\bigcup_n A_n=A$,则 $P(A_n)\uparrow P(A)$。
这些都是可列可加性结合单调性直接给出的标准结论(可在教材中找到详尽证明)。
条件概率与乘法法则
条件概率 $P(A\mid B)$(严格定义)
在概率空间 $(\Omega,\mathcal F,P)$ 中,若 $P(B)>0$,定义
$$ P(A\mid B)\;\;\stackrel{\text{def}}=\;\;\frac{P(A\cap B)}{P(B)}. $$直观含义:在“已知 $B$ 发生”的世界里,$A$ 的相对概率。
严格性质(把 $P(\cdot\mid B)$ 看作固定 $B$ 后的“新概率测度”):
非负性:$P(A\mid B)\ge 0$;
规范化:$P(\Omega\mid B)=\dfrac{P(\Omega\cap B)}{P(B)}=\dfrac{P(B)}{P(B)}=1$;
可列可加性:若 $\{A_i\}$ 两两不交,则
$$ P\Big(\bigcup_i A_i\;\Big|\;B\Big)=\frac{P\big((\bigcup_i A_i)\cap B\big)}{P(B)} =\frac{\sum_i P(A_i\cap B)}{P(B)}=\sum_i P(A_i\mid B). $$
因此 $P(\cdot\mid B)$ 满足 Kolmogorov 公理,是条件下的概率测度。
注:当 $P(B)=0$ 时,上式失效;更一般情形要用“正则条件概率”(Radon–Nikodym 定理给出存在性),离散情形无需担心。
联合概率 $P(A\cap B)$ 与乘法法则
由定义立刻得到乘法法则:
$$ \boxed{\,P(A\cap B)=P(A\mid B)\,P(B)\,}\qquad(P(B)>0) $$同理也有 $P(A\cap B)=P(B\mid A)\,P(A)$(若 $P(A)>0$)。
链式法则(多事件):对 $A_1,\dots,A_n$,若各条件概率有定义,
$$ P\Big(\bigcap_{k=1}^n A_k\Big) = P(A_1)\cdot P(A_2\mid A_1)\cdot P(A_3\mid A_1\cap A_2)\cdots P(A_n\mid A_1\cap\cdots\cap A_{n-1}). $$连续/离散变量版:$f_{X,Y}(x,y)=f_{X\mid Y}(x\mid y)f_Y(y)$;离散时 $p_{X,Y}(x,y)=p_{X\mid Y}(x\mid y)p_Y(y)$。
示例
示例A:抽牌(不放回)
标准 52 张牌,记
- $A_1=\{\text{第一张是 A(ace)}\}$
- $A_2=\{\text{第二张是 A}\}$
目标:$P(A_1\cap A_2)$。
按乘法法则:$P(A_1\cap A_2)=P(A_1)\cdot P(A_2\mid A_1)$。
示例 B:医学检测(Bayes 由乘法法则引出)
设:
- 患病先验(流行率)$\pi=P(D)$
- 灵敏度 $Se=P(T^+\mid D)$
- 特异度 $Sp=P(T^-\mid \bar D)\Rightarrow P(T^+\mid \bar D)=1-Sp$
阳性预测值(PPV):
$$ P(D\mid T^+)=\frac{P(T^+\mid D)P(D)}{P(T^+)} =\frac{Se\cdot \pi}{Se\cdot \pi+(1-Sp)\cdot (1-\pi)}. $$这只是把乘法法则代回、并用全概率 $P(T^+)=P(T^+\mid D)\pi+P(T^+\mid \bar D)(1-\pi)$。
小结
- 定义:$P(A\mid B)=P(A\cap B)/P(B)$;它本身是概率测度。
- 乘法:$P(A\cap B)=P(A\mid B)P(B)$。推广成链式法则。
- 应用:抽牌/不放回、医学检测都直接用乘法法则;Bayes 公式=乘法法则 + 全概率。
全概率公式与贝叶斯定理
全概率公式(Law of Total Probability, LTP)
严格表述(离散/可列划分)
设 $(\Omega,\mathcal F,P)$ 为概率空间,$\{B_i\}_{i\in I}\subset\mathcal F$ 构成对 $\Omega$ 的可列划分(两两不交且并为 $\Omega$),并且 $P(B_i)>0$。对任意事件 $A\in\mathcal F$,
$$ \boxed{P(A)=\sum_{i\in I} P(A\mid B_i)\,P(B_i).} $$证明(由可列可加性 + 条件概率定义)
因为 $\{B_i\}$ 划分 $\Omega$,有
$$ A=\bigcup_{i}(A\cap B_i),\qquad (A\cap B_i)\ \text{两两不交}. $$由可列可加性,
$$ P(A)=\sum_i P(A\cap B_i)=\sum_i \frac{P(A\cap B_i)}{P(B_i)}\,P(B_i)=\sum_i P(A\mid B_i)\,P(B_i). $$连续型/密度版(常用等式)
若 $(X,Y)$ 有联合密度 $f_{X,Y}$,则
$$ \boxed{f_X(x)=\int f_{X\mid Y}(x\mid y)\,f_Y(y)\,dy,} $$这是“对所有 $y$”的条件密度按边缘 $f_Y$ 加权的总和;对事件 $A$ 则
$$ P(X\in A)=\int P(X\in A\mid Y=y)\,f_Y(y)\,dy. $$(更一般地,条件概率可由 Radon–Nikodym 定理给出,这里不展开。)
# 画一个概率树(tree diagram)来展示全概率公式的计算路径
import matplotlib.pyplot as plt
# 数据
labels = [
"患病", "健康",
"阳性(病)", "阴性(病)",
"阳性(健康)", "阴性(健康)"
]
probs = [
p_disease, 1 - p_disease,
p_test_pos_given_disease, 1 - p_test_pos_given_disease,
p_test_pos_given_healthy, 1 - p_test_pos_given_healthy
]
# 简单画树
fig, ax = plt.subplots(figsize=(8,5))
ax.axis("off")
# 第一层
ax.text(0.05, 0.5, "总体", fontsize=12, ha="center")
ax.plot([0.1, 0.3], [0.5, 0.7], 'k-')
ax.plot([0.1, 0.3], [0.5, 0.3], 'k-')
# 第二层
ax.text(0.35, 0.7, f"患病\n({p_disease:.2f})", ha="center")
ax.text(0.35, 0.3, f"健康\n({1-p_disease:.2f})", ha="center")
ax.plot([0.4, 0.6], [0.7, 0.8], 'k-')
ax.plot([0.4, 0.6], [0.7, 0.6], 'k-')
ax.plot([0.4, 0.6], [0.3, 0.4], 'k-')
ax.plot([0.4, 0.6], [0.3, 0.2], 'k-')
# 第三层
ax.text(0.65, 0.8, f"阳性\n({p_test_pos_given_disease:.2f})", ha="center")
ax.text(0.65, 0.6, f"阴性\n({1-p_test_pos_given_disease:.2f})", ha="center")
ax.text(0.65, 0.4, f"阳性\n({p_test_pos_given_healthy:.2f})", ha="center")
ax.text(0.65, 0.2, f"阴性\n({1-p_test_pos_given_healthy:.2f})", ha="center")
plt.show()
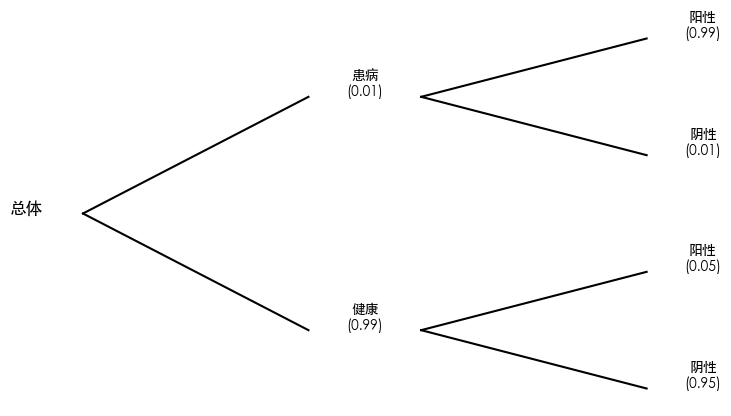
# 用医学检测的场景来模拟:
# 1. 疾病的先验概率很低
# 2. 检测有一定的准确率
# 下面代码直接体现了 "把总体划分为互斥的几类事件,然后求和" 的思想。
import numpy as np
# 参数
p_disease = 0.01 # 患病率:P(病)
p_test_pos_given_disease = 0.99 # 患病检测为阳性的概率:P(阳性|病)
p_test_pos_given_healthy = 0.05 # 健康误判为阳性的概率:P(阳性|健康)
# 全概率公式:
# P(测试阳性) = P(阳性|病)P(病) + P(阳性|健康)P(健康)
p_positive = (p_test_pos_given_disease * p_disease +
p_test_pos_given_healthy * (1 - p_disease))
print(f"P(测试阳性) = {p_positive:.4f}")
P(测试阳性) = 0.0594
贝叶斯定理(Bayes’ Theorem)
基本式(两事件)
若 $P(B)>0$,
$$ \boxed{P(A\mid B)=\frac{P(B\mid A)\,P(A)}{P(B)}.} $$由乘法法则 $P(A\cap B)=P(A\mid B)P(B)=P(B\mid A)P(A)$ 直接得到。
把分母用全概率展开($\{A,\bar A\}$ 划分):
$$ P(B)=P(B\mid A)P(A)+P(B\mid \bar A)P(\bar A), $$故
$$ P(A\mid B)=\frac{P(B\mid A)P(A)} {P(B\mid A)P(A)+P(B\mid \bar A)(1-P(A))}. $$多假设版(可列划分 $\{H_i\}$)
$$ \boxed{P(H_i\mid E)=\frac{P(E\mid H_i)\,P(H_i)}{\sum_j P(E\mid H_j)\,P(H_j)}.} $$连续/密度版
$$ \boxed{f_{\Theta\mid X}(\theta\mid x)=\frac{f_{X\mid \Theta}(x\mid \theta)\,\pi(\theta)}{\int f_{X\mid \Theta}(x\mid t)\,\pi(t)\,dt}}, $$其中 $\pi(\theta)$ 为先验密度,分母是证据(边缘似然)。
“反转因果”的力量(diagnostic vs. causal)
- 似然 $P(E\mid H)$:因果向前(假设 $H$ 为真,会多大概率看到证据 $E$?)
- 后验 $P(H\mid E)$:诊断反推(观察到证据 $E$,究竟多大概率是由 $H$ 引起?)
二者不对称:$P(E\mid H)$ 大并不意味着 $P(H\mid E)$ 大。必须结合先验(基率)用贝叶斯公式反转:
$$ \text{后验 odds}=\text{先验 odds}\times \underbrace{\frac{P(E\mid H)}{P(E\mid \bar H)}}_{\text{Bayes 因子 / 似然比}}. $$这就是为什么**基率忽视(base-rate fallacy)**会导致严重误判。
# 用上一步算出来的 P(测试阳性),再反推“阳性时真的有病的概率”:
# 贝叶斯定理:
# P(病|阳性) = [P(阳性|病) * P(病)] / P(阳性)
p_disease_given_positive = (p_test_pos_given_disease * p_disease) / p_positive
print(f"P(病|阳性) = {p_disease_given_positive:.4f}")
# 这个数值会明显比直觉的小(因为先验概率低 + 假阳性率存在),体现了 "反转因果关系" 的力量。
P(病|阳性) = 0.1667
应用示例
垃圾邮件识别(Naive Bayes 思想)
设 $H\in\{\text{spam},\text{ham}\}$,特征 $E=(w_1,\dots,w_d)$ 表示邮件中若干词是否出现。朴素贝叶斯假设条件独立:
$$ P(E\mid H)=\prod_{k=1}^d P(w_k\mid H). $$后验:
$$ P(\text{spam}\mid E)=\frac{\left(\prod_k P(w_k\mid \text{spam})\right)P(\text{spam})} {\sum_{h\in\{\text{spam},\text{ham}\}}\left(\prod_k P(w_k\mid h)\right)P(h)}. $$直觉:某些“强指示词”让 $P(E\mid \text{spam})$ 远大于 $P(E\mid \text{ham})$,乘上先验 $P(\text{spam})$ 后使后验偏向 spam。
小练习(先不算数值):如果黑名单域名出现(特征 $w$),解释为何“似然比” $\frac{P(w\mid \text{spam})}{P(w\mid \text{ham})}$ 是判别力的关键?
故障诊断(多假设贝叶斯)
假设设备有三种互斥故障 $H_1,H_2,H_3$ 和“正常” $H_0$,先验 $\{P(H_i)\}$ 已知。传感器读数 $E$ 的分布 $P(E\mid H_i)$ 已知(或可近似为正态、指数等)。观测到 $E=e$ 后:
$$ P(H_i\mid e)=\frac{P(e\mid H_i)P(H_i)}{\sum_{j=0}^3 P(e\mid H_j)P(H_j)}. $$直觉:哪一个 $H_i$ 既更常发生(大先验),又更能产生当前观测(大似然),就占据更大后验。
小结
- 全概率:把“情况”可列划分后,“总概率 = 条件概率 × 权重”的加权和。
- 贝叶斯:后验 $\propto$ 似然 × 先验;分母是证据的全概率。
- 反转因果:用 $P(E\mid H)$ 反推 $P(H\mid E)$,必须乘上先验;最好用似然比/odds 思考。
独立性与条件独立
严谨定义与等价刻画
事件独立(Independence)
在概率空间 $(\Omega,\mathcal F,P)$ 中,事件 $A,B\in\mathcal F$ 独立指
$$ \boxed{P(A\cap B)=P(A)\,P(B).} $$若 $P(B)>0$,等价于
$$ P(A\mid B)=\frac{P(A\cap B)}{P(B)}=P(A). $$指标函数刻画:令 $1_A,1_B$ 为指示函数,则独立 $\iff\ \mathbb E[1_A1_B]=\mathbb E[1_A]\mathbb E[1_B]$。
多事件独立(mutual independence):$\{A_i\}_{i=1}^n$ 互相独立指任何子集的交满足乘法,例如
$$ P\!\Big(\bigcap_{i\in S} A_i\Big)=\prod_{i\in S}P(A_i)\quad(\forall S\subset\{1,\dots,n\},S\neq\varnothing). $$注意:“两两独立”不等于“共同独立”。
与“不相交”不同:若 $A\cap B=\varnothing$ 且 $P(A),P(B)>0$,则 $P(A\cap B)=0\ne P(A)P(B)$,故不可能独立。
# 一个简单例子:掷两个公平骰子,事件 A 是“第一个骰子是 6”,事件 B 是“第二个骰子是 6”。
import numpy as np
# 模拟次数
N = 1_000_000
# 掷两个骰子
die1 = np.random.randint(1, 7, N)
die2 = np.random.randint(1, 7, N)
# 定义事件
A = (die1 == 6)
B = (die2 == 6)
# 计算概率
P_A = A.mean()
P_B = B.mean()
P_A_and_B = (A & B).mean()
print("P(A) =", P_A)
print("P(B) =", P_B)
print("P(A ∩ B) =", P_A_and_B)
print("P(A)*P(B) =", P_A * P_B)
# 理论上:P(A) = 1/6 = 0.1666666667, P(B) = 1/6 = 0.1666666667, P(A∩B) = 1/36 = 0.02777777778 = P(A)P(B)。
# 如果运行结果接近理论值,说明 A 和 B 独立。
P(A) = 0.16706
P(B) = 0.166036
P(A ∩ B) = 0.02781
P(A)*P(B) = 0.027737974159999994
条件独立(Conditional independence)
给定 σ-代数 $\mathcal G$(或给定随机变量/事件 $C$ 生成的 $\sigma(C)$),称在 $\mathcal G$ 条件下 $A,B$ 独立,若
$$ \boxed{\mathbb E[1_A1_B\,\mid\,\mathcal G]=\mathbb E[1_A\,\mid\,\mathcal G]\ \mathbb E[1_B\,\mid\,\mathcal G]\quad\text{a.s.}} $$等价地(在 $P(C)>0$ 的离散情形常用)
$$ \boxed{P(A\cap B\mid C)=P(A\mid C)\,P(B\mid C)\quad\text{(对几乎所有 }C\text{ 取值)}.} $$重要关系:
- 条件独立 不蕴含 无条件独立;无条件独立也 不蕴含 条件独立。
- 常见结构:共同原因 $C$ 会让 $A,B$ 相关;对 $C$ 条件化后往往变得“更独立”。相反,对共同结果(collider)条件化会“引入”相关(Berkson 悖论)。
# 假设我们有一个感应灯系统:
# 事件 A:室内有人
# 事件 B:灯亮
# 条件 C:外面天黑
# 我们模拟一种情况:天黑时,灯亮与否只取决于“室内有人”这个条件,且在天黑情况下,人和灯的状态互不影响——这就是条件独立。
# 模拟次数
N = 1_000_000
# 条件 C:天黑
C = np.random.rand(N) < 0.5 # 50% 概率天黑
# 在天黑情况下,有人的概率和灯亮的概率
A_given_C = np.random.rand(N) < 0.6 # 天黑时有人概率 0.6
B_given_C = np.random.rand(N) < 0.7 # 天黑时灯亮概率 0.7
# 在天亮情况下(~C),人为 0.3 概率,灯亮 0.1 概率
A_given_notC = np.random.rand(N) < 0.3
B_given_notC = np.random.rand(N) < 0.1
# 根据 C 赋值
A = np.where(C, A_given_C, A_given_notC)
B = np.where(C, B_given_C, B_given_notC)
# 计算条件概率
mask_C = C # 只考虑天黑的情况
P_A_and_B_given_C = (A & B & mask_C).sum() / mask_C.sum() # P(A ∩ B | C) = P(A ∩ B ∩ C) / P(C)
P_A_given_C = (A & mask_C).sum() / mask_C.sum() # P(A|C)
P_B_given_C = (B & mask_C).sum() / mask_C.sum() # P(B|C)
print("P(A ∩ B | C) =", P_A_and_B_given_C)
print("P(A|C) * P(B|C) =", P_A_given_C * P_B_given_C)
# 如果 P(A ∩ B | C) ≈ P(A|C) * P(B|C),说明 A 与 B 在 C 条件下是条件独立的。
P(A ∩ B | C) = 0.420284111266571
P(A|C) * P(B|C) = 0.4200211083400713
两个严谨小推论
(i) 独立 ⇒ 条件概率不变 若 $A\perp B$ 且 $P(B)>0$,则 $P(A\mid B)=P(A)$。
(ii) 条件独立 + 全概率 若给定 $\mathcal G$ 有 $A\perp B\mid \mathcal G$,则
$$ P(A\cap B)=\mathbb E\!\big[\,P(A\cap B\mid\mathcal G)\,\big] =\mathbb E\!\big[\,P(A\mid\mathcal G)\,P(B\mid\mathcal G)\,\big]. $$除非 $P(A\mid\mathcal G)$ 是常数(即与 $\mathcal G$ 无关),否则一般 $\mathbb E[XY]\neq \mathbb E[X]\mathbb E[Y]$,所以无条件通常不独立。
示例
示例 A:遗传性状(“同因导致相关;给定因独立”)
设 $C$ 表示父母的基因型;$A$、$B$ 表示两个兄弟是否具有某隐性表型(事件)。经典遗传模型下,给定父母基因型 $C$,两个孩子的表型是条件独立的:
$$ A\perp B\ \mid\ C,\qquad P(A\cap B)=\mathbb E\!\big[P(A\mid C)\,P(B\mid C)\big]. $$直觉:兄弟相似是因为“共同原因”——父母基因;一旦把父母基因固定,兄弟间剩下的是独立的孟德尔分离。
但边际下 $A,B$ 往往相关(不独立):不同家庭 $C$ 的分布不同,使 $P(A\mid C)$ 在总体上有波动。
示例 B:感应灯系统(“共同原因”导致相关;条件化后独立)
建模:
- $C\in\{0,1\}$:是否有人经过(先验 $P(C=1)=\pi$)。
- 两个传感器事件:$A=\{\text{传感器1触发}\}$, $B=\{\text{传感器2触发}\}$。
- 传感器性能:灵敏度 $Se=P(A=1\mid C=1)=P(B=1\mid C=1)=s$;误报率 $Fa=P(A=1\mid C=0)=P(B=1\mid C=0)=f$。条件上独立:
结论:
$$ P(A\cap B)=s^2\pi + f^2(1-\pi),\quad P(A)=s\pi+f(1-\pi). $$一般 $P(A\cap B)\ne P(A)P(B)$(所以 $A,B$ 不独立);但给定 $C$ 时
$$ P(A\cap B\mid C)=P(A\mid C)\,P(B\mid C), $$即条件独立成立。直觉:是否有人这个“共同原因”解释了两传感器一起响的相关性。
常见误区速记
- 互斥 ≠ 独立(除非至少一个概率为 0)。
- 两两独立 ≠ 共同独立(要检查所有交集)。
- 相关性(如协方差)为 0 并不保证独立(非高斯情形)。
- 条件化可打破或产生独立性(取决于是“共同因”还是“共同果”)。