为什么要“不对称”? (The Motivation)
- 回顾限制: Metropolis 算法要求 $Q(x|y) = Q(y|x)$(像个醉汉,往左往右概率一样)。
- 现实痛点:
- 边界问题: 如果变量必须大于 0(比如身高、价格),用对称的高斯分布去跳,总会跳到负数区被拒绝,效率极低。
- 聪明移动: 如果我们知道山顶大概在东方,我们能不能让 $Q$ 偏向东方跳?(引入有偏见的 $Q$)。
- 核心冲突: 一旦 $Q$ 不对称,原来的细致平衡就被打破了,怎么修补?
在原始 Metropolis 中,提议分布 $Q$ 必须满足 对称性 (Symmetry):
$$Q(x_{new} | x_{old}) = Q(x_{old} | x_{new})$$这意味着:从 A 跳到 B 的概率,必须完全等于从 B 跳回 A 的概率。(比如:往左跳 1 米和往右跳 1 米,概率必须一样。)这听起来很公平,但在实际应用中,这种“公平”往往意味着低效,甚至是灾难。
现实痛点
痛点 1:边界问题 (The “Wall” Problem)
现实世界中,很多变量是有物理限制的。
- 例子: 假设你在模拟人的身高、红细胞数量或者商品价格。这些数值必须是 正数 ($x > 0$)。
- Metropolis 的尴尬: 假设你现在处于 $x=0.1$(很靠近 0)。你用一个对称的高斯分布去跳。
- 有 50% 的概率,你会跳到负数(比如 -0.5)。
- 因为目标分布 $\pi(x)$ 在负数区是 0,这次提议会被直接拒绝。
- 结果: 在边界附近,你的采样器有一半的时间都在“撞墙”,计算资源被大量浪费。
import numpy as np
# 1. 设定目标:指数分布 (必须 > 0)
def target_pi(x):
if x < 0:
return 0 # 边界!
return np.exp(-x)
# 2. 模拟参数
current_x = 0.1 # 当前位置非常靠近边界
sigma = 1.0 # 步长比较大
n_trials = 1000 # 尝试提议 1000 次
rejected_by_wall = 0
valid_proposals = 0
print(f"--- 开始模拟:当前位置 x = {current_x} ---")
# 3. 看看“对称提议”会发生什么
for i in range(n_trials):
# 对称的高斯提议 (Symmetric Gaussian Proposal)
proposal_x = np.random.normal(current_x, sigma)
# 检查是否“撞墙”
if proposal_x < 0:
rejected_by_wall += 1
else:
valid_proposals += 1
print(f"尝试总次数: {n_trials}")
print(f"撞墙次数 (跳到负数区): {rejected_by_wall}")
print(f"有效提议次数: {valid_proposals}")
print(f"⚠️ 浪费率: {rejected_by_wall / n_trials * 100:.1f}%")
--- 开始模拟:当前位置 x = 0.1 ---
尝试总次数: 1000
撞墙次数 (跳到负数区): 451
有效提议次数: 549
⚠️ 浪费率: 45.1%
我们想要什么?
我们希望有一个“聪明的向导”,在边界附近时,能自动建议我们:“嘿,后面是墙,我们只往正方向跳吧!”这就需要一个不对称的分布(比如对数正态分布 Log-Normal),它只会生成正数。
痛点 2:高维空间的迷路 (The High-Dim Maze)
在二维平面上,“醉汉随机乱跳”可能还能凑合。但在 100 维空间里,随机乱跳几乎等于找死。
- Metropolis 的尴尬: 它的 $Q$ 是盲目的。它不知道哪里是山峰(高概率区)。它只是向四周均匀地发射探测器。
- 结果: 在高维空间,绝大多数方向都是“下坡路”(概率极低)。如果你盲目乱跳,你的提议会被疯狂拒绝,导致接受率极低,采样器卡在原地不动。
import numpy as np
def run_simulation(dim):
# 目标:标准正态分布
# 提议:对称的高斯游走
n_steps = 1000
current_x = np.zeros(dim) # 从原点出发
accepted = 0
step_size = 0.5 # 固定的步长
for _ in range(n_steps):
# 1. 盲目地向四周随机跳一步 (Symmetric)
proposal_x = current_x + np.random.normal(0, step_size, size=dim)
# 2. 计算接受率 (Metropolis 简化版)
# log 形式计算防止数值溢出
# log_ratio = -0.5 * (new^2 - old^2)
log_ratio = -0.5 * (np.sum(proposal_x**2) - np.sum(current_x**2))
# 接受/拒绝
if np.log(np.random.rand()) < log_ratio:
current_x = proposal_x
accepted += 1
return accepted / n_steps
print("--- 高维空间的迷路测试 (固定步长 0.5) ---")
# 测试 2D
acc_rate_2d = run_simulation(dim=2)
print(f"维度 = 2 时的接受率: {acc_rate_2d * 100:.1f}% (非常健康)")
# 测试 100D
acc_rate_100d = run_simulation(dim=100)
print(f"维度 = 100 时的接受率: {acc_rate_100d * 100:.1f}% (几乎卡死)")
print("\n结论:在高维空间,如果不使用梯度指引方向,盲目乱跳几乎总是会被拒绝。")
--- 高维空间的迷路测试 (固定步长 0.5) ---
维度 = 2 时的接受率: 72.6% (非常健康)
维度 = 100 时的接受率: 0.0% (几乎卡死)
结论:在高维空间,如果不使用梯度指引方向,盲目乱跳几乎总是会被拒绝。
我们想要什么?
我们希望利用 梯度 (Gradient) 信息。如果知道东边是上坡,我们就让 $Q$ 往东跳的概率大一点(比如 80%),往西跳的概率小一点(20%)。这显然打破了对称性:$Q(A \to B) \neq Q(B \to A)$。
核心冲突:不对称带来的“流量危机”
那么,如果现在我们决定引入“不对称”的 $Q$(比如我们偏向于往山顶跳)。
但这带来了一个严重的数学危机:细致平衡 (Detailed Balance) 被破坏了。
让我们想象两个城市:低城 (Low City, A) 和 高城 (High City, B)。
- 原来的 Metropolis (对称):
- 路修得一样宽。从 A 去 B 的车道,和从 B 回 A 的车道一样多。
- 系统靠 $\pi(B) > \pi(A)$ 这个自然吸引力来调节人口。
- 现在的 MH (不对称/有偏见):
- 你为了让小人更快爬山,你人为地修了一条从 A 到 B 的高速公路($Q(B|A)$ 很大)。
- 同时,你把从 B 回 A 的路变成了羊肠小道($Q(A|B)$ 很小)。
后果:如果不加干预,所有人都会顺着高速公路涌向 B,并且很难从 B 回来。最终,系统在 B 处积压的人口会远超 $\pi(B)$ 应有的比例。你的采样结果这就 失真了(Over-represented the high probability region)。
💡 破局思路
我们想要“不对称提议”带来的效率(不撞墙、指引方向),但又不想失去“细致平衡”带来的准确性。
怎么办?
既然 $Q$(提议)这边的交通流已经变得不平衡了(去程容易回程难),我们就必须在 $\alpha$ (接受率/海关) 那里找补回来。
- 如果去程的路太顺了($Q$ 偏大),那海关($\alpha$)就要严一点,多拒签一些人。
- 如果回程的路太难走($Q$ 偏小),那海关($\alpha$)就要宽一点,多放行一些人。
这就是 Metropolis-Hastings 算法诞生的那一刻:通过修改接受率公式,来抵消提议分布的不对称性。
哈斯廷斯的修正 (The Hastings Correction)
核心公式:从 Metropolis 到 MH
回顾一下,我们的目标是构造一个满足 细致平衡 的马尔可夫链:
$$\pi(x) \cdot Q(x \to x') \cdot \alpha(x \to x') = \pi(x') \cdot Q(x' \to x) \cdot \alpha(x' \to x)$$(当前概率 $\times$ 提议概率 $\times$ 接受率 = 逆向的三个量)
在 Metropolis 中,因为 $Q$ 是对称的($Q(x \to x') = Q(x' \to x)$),中间那一项直接消掉了。
但在 MH 中,因为 $Q$ 不对称,我们必须把 $Q$ 保留下来。经过推导,Hastings 给出的新的接受率公式如下:
$$\alpha = \min\left(1, \underbrace{\frac{\pi(x_{new})}{\pi(x_{old})}}_{\text{目标比率}} \times \underbrace{\frac{Q(x_{old}|x_{new})}{Q(x_{new}|x_{old})}}_{\text{哈斯廷斯修正项}} \right)$$这个新增的 修正项 (Correction Term):
- 分母 ($Q_{new}|Q_{old}$):是正向跳过去的概率。
- 分子 ($Q_{old}|Q_{new}$):是逆向跳回来的概率。
这个修正项的意思是:“如果你跳过去很容易,但跳回来很难,那我就要降低你的通过率,以此来维持平衡。”
直观理解:城市与高速公路 🏙️🛣️
用一个 **“人口流动模型”**来类比。场景设定如下:
- 城市 A (小镇): 目标人口 $\pi(A) = 100$。
- 城市 B (大都会): 目标人口 $\pi(B) = 200$。
- 平衡目标: 我们希望 B 的人口始终是 A 的 2 倍 ($\frac{\pi(B)}{\pi(A)} = 2$)。
不对称的道路 ($Q$)。现在,你设计了一个极其不对称的交通系统:
- A $\to$ B (高速公路): 非常容易走。$Q(B|A) = 0.9$ (90% 的人都想去大城市)。
- B $\to$ A (泥泞小路): 非常难走。$Q(A|B) = 0.1$ (只有 10% 的人想回小镇)。
如果不加修正 (原始 Metropolis):
- 接受率只看人口吸引力:$\alpha = \min(1, \frac{200}{100}) = 1$。
- 后果: 人们疯狂地通过高速公路涌向 B,但很少有人能从 B 回来。不久之后,B 的人口会爆炸,变成 A 的 100 倍,而不是 2 倍。细致平衡崩溃。
加上哈斯廷斯修正 (MH 算法):让我们看看修正项是如何作为 “交通管制员” 介入的。
情况 1:有人想从 A 去 B (走高速公路)
$$ \alpha(A \to B) = \min\left(1, \frac{200}{100} \times \frac{0.1 \text{ (回程难)}}{0.9 \text{ (去程易)}} \right) \\ \alpha = \min\left(1, 2 \times 0.11 \right) = \mathbf{0.22} $$- 解读: 虽然 B 城市更有吸引力(2倍),但因为去 B 的路太容易了(不对称),如果放任不管就会失衡。所以海关狠狠地砍了一刀,只批准 22% 的人通行。
情况 2:有人想从 B 回 A (走泥泞小路)
$$ \alpha(B \to A) = \min\left(1, \frac{100}{200} \times \frac{0.9 \text{ (回程易)}}{0.1 \text{ (去程难)}} \right)\\ \alpha = \min\left(1, 0.5 \times 9 \right) = \min(1, 4.5) = \mathbf{1} $$- 解读: 虽然 A 城市没什么吸引力(0.5倍),但因为回 A 的路太难走了,几乎没人愿意尝试。所以海关规定:只要有人愿意回 A,统统放行! (100% 接受)。
结果:通过严控“容易的路”,放宽“艰难的路”,人口流动最终在 A 和 B 之间达成了完美的 1:2 动态平衡。
数学证明:为什么它刚好能平衡?(The Proof)
我们要证明以下等式成立(细致平衡):
$$\pi(x) Q(x'|x) \alpha(x \to x') = \pi(x') Q(x|x') \alpha(x' \to x)$$假设 $x'$ 是那个“更好”的状态(即 $\pi(x') Q(x|x') > \pi(x) Q(x'|x)$,这一边更有优势)。
- 看左边 (从 $x$ 跳到 $x'$):根据公式,这一侧处于劣势,所以接受率 $\alpha(x \to x') = 1$(完全接受)。$$\text{Left Flow} = \pi(x) \cdot Q(x'|x) \cdot 1$$
- 看右边 (从 $x'$ 跳回 $x$):这一侧处于优势,所以接受率需要修正:$$\alpha(x' \to x) = \frac{\pi(x)}{\pi(x')} \times \frac{Q(x'|x)}{Q(x|x')}$$那么右边的流量是:$$\text{Right Flow} = \pi(x') \cdot Q(x|x') \cdot \left( \frac{\pi(x)}{\pi(x')} \frac{Q(x'|x)}{Q(x|x')} \right)$$
- 奇迹般的抵消:注意看右边的式子,$\pi(x')$ 和 $Q(x|x')$ 全部抵消了!$$\text{Right Flow} = \pi(x) \cdot Q(x'|x)$$
- 结论:$$\text{Left Flow} = \text{Right Flow}$$
证毕。✅
实战中的 $Q$ (The Choice of Proposals)
哈斯廷斯修正公式意味着,只要算出那个修正项,就可以使用任何提议分布 $Q$!
| 你的困境 | 推荐的 $Q$ | 修正项 $\frac{Q(x\|x')}{Q(x'\|x)}$ |
|---|---|---|
| 标准情况 (无边界) | 对称高斯游走 (Symmetric Random Walk) | 1 (不用算,直接消掉) |
| 有边界约束 (如 $x > 0$) | 对数正态游走 (Log-Normal Walk) | $\frac{x_{new}}{x_{old}}$ (极为简单) |
| 高维复杂地形 | MALA / HMC (Langevin Dynamics) | 复杂公式 (但计算机能算) |
独立采样器 (Independent Sampler)
完全不看脚下,直接根据猜测的新分布乱跳。
这是最极端的一种设计。
- 规则: $Q(x_{new} | x_{old}) = Q(x_{new})$。无论你现在在哪,我都完全忽略,$x_{new}$ 是从一个固定的全局分布里抽出来的。
- 适用场景: 当你对目标分布 $\pi$ 已经有一个大概的了解,能构造出一个跟 $\pi$ 长得很像的 $Q$ 时。
- 修正项简化:$$\frac{Q(x_{old})}{Q(x_{new})}$$
- 接受率变为:$$\alpha = \min\left(1, \frac{\pi(x_{new}) / Q(x_{new})}{\pi(x_{old}) / Q(x_{old})} \right) = \min\left(1, \frac{w_{new}}{w_{old}} \right)$$(这里的 $w = \pi/Q$ 叫权重)
- 评价:
- 优点: 如果 $Q$ 选得好(跟 $\pi$ 很像),收敛速度极快,几步就能遍历全图。
- 缺点: 只要 $\pi$ 有一点点地方比 $Q$ “胖”(Q 覆盖不住的地方),算法就会在那里卡死极长时间。高维空间中极其危险。
对数正态游走 (Log-normal Walk)
专门用于处理必须为正数的变量(解决边界问题)。
我们不再用 $x_{new} = x_{old} + \text{Noise}$,而是用乘法或者对数空间的加法。
- 规则:$$\ln(x_{new}) \sim \text{Normal}(\ln(x_{old}), \sigma^2)$$也就是说,我们在“对数尺度”上进行对称游走,但在“原始尺度”上,这完全是不对称的。
- 为什么是不对称的?
- 从 1 跳到 2 的概率,不等于 从 2 跳到 1 的概率。
- 对数正态分布的形状是“左边陡,右边拖尾”。
- 数学推导(省略过程,直接给结论):$Q(x'|x)$ 正比于 $\frac{1}{x'}$。
- 修正项(非常优雅):$$\frac{Q(x_{old}|x_{new})}{Q(x_{new}|x_{old})} = \frac{x_{new}}{x_{old}}$$
- 直观理解修正项:
- 因为对数正态分布倾向于往“大数值”的方向扩散(右偏)。
- 如果你提议了一个很大的 $x_{new}$(跳得远了),修正项 $\frac{x_{new}}{x_{old}} > 1$ 会奖励这次跳跃,增加接受率。
- 这完美抵消了分布本身的偏差。
MALA (Metropolis-Adjusted Langevin Algorithm)
利用梯度信息,让 $Q$ 总是倾向于往概率高的地方“漂移”。
这是现代机器学习(如贝叶斯神经网络)中最常用的高级策略。它是解决第一阶段“高维迷路”痛点的神器。
- 直觉:与其盲目乱跳,不如算一下目标分布的梯度 $\nabla \log \pi(x)$(地形的坡度)。
- 如果东边是上坡,那我就给 $Q$ 加一个向东的 “漂移力” (Drift)。
- 规则:$$x_{new} = x_{old} + \underbrace{\frac{\tau}{2} \nabla \log \pi(x_{old})}_{\text{向高处漂移}} + \underbrace{\sqrt{\tau} \xi}_{\text{随机噪声}}$$(这就好比:我想往山顶走,但我还是喝醉了,所以走得歪歪扭扭)
- 为什么需要 MH 修正? 虽然是往高处走,但因为我们需要把连续的时间离散化(步长 $\tau$),这会引入误差。如果不加修正,最后采样的分布会略微偏离真实的 $\pi$。MH 的修正项在这里起到了“纠错”的作用,确保即使步长没设好,最终结果也是精确的 $\pi$。
代码实战 (Python Implementation)
- 任务: 模拟一个经典的 Gamma 分布(形状类似钟形,但左边被 0 截断,右边拖尾)
- 对比实验:
- 方案 A:Naive Metropolis。对称高斯游走(虽然对,但在边界处效率低)。
- 方案 B:Broken MH (错误示范)。用了不对称的 Log-Normal 提议,但是忘记加修正项。
- 预期后果: 因为 Log-Normal 倾向于往数值大的方向跳,如果不加修正,样本会整体向右偏移(偏大)。
- 方案 C:orrect MH (正确示范): 用 Log-Normal 提议,并且加上修正项。
- 预期后果: 完美贴合。
import numpy as np
import matplotlib.pyplot as plt
# --- 1. 设定目标分布 ---
# Gamma 分布 (必须 > 0)
def target_pi(x):
# 使用 np.where 修复之前的报错
return np.where(x <= 0, 0, x * np.exp(-x / 2))
# --- 场景 A: Naive Metropolis (撞墙选手) ---
def run_naive_metropolis(n_samples, sigma=1.0):
samples = []
current_x = 2.0
wall_hits = 0 # 计数器:记录撞墙次数
for _ in range(n_samples):
# 对称提议:可能跳到负数
proposal_x = np.random.normal(current_x, sigma)
# 撞墙检查
if proposal_x <= 0:
alpha = 0
wall_hits += 1 # 记录撞墙
else:
alpha = min(1, target_pi(proposal_x) / target_pi(current_x))
if np.random.rand() < alpha:
current_x = proposal_x
samples.append(current_x)
return samples, wall_hits
# --- 场景 B: Broken MH (有偏见,无修正) ---
def run_broken_mh(n_samples, sigma=1.0):
samples = []
current_x = 2.0
# LogNormal 永远大于 0,所以不会撞墙,不需要 wall_hits 计数
for _ in range(n_samples):
# 不对称提议 (倾向于变大)
proposal_x = np.random.lognormal(np.log(current_x), sigma)
# ❌ 错误核心:只计算概率比,忘记乘修正项!
ratio_pi = target_pi(proposal_x) / target_pi(current_x)
alpha = min(1, ratio_pi)
if np.random.rand() < alpha:
current_x = proposal_x
samples.append(current_x)
return samples
# --- 场景 C: Correct MH (有偏见,有修正) ---
def run_correct_mh(n_samples, sigma=1.0):
samples = []
current_x = 2.0
for _ in range(n_samples):
# 不对称提议
proposal_x = np.random.lognormal(np.log(current_x), sigma)
# ✅ 正确核心:加上 Hastings 修正项 (new / old)
ratio_pi = target_pi(proposal_x) / target_pi(current_x)
correction = proposal_x / current_x
alpha = min(1, ratio_pi * correction)
if np.random.rand() < alpha:
current_x = proposal_x
samples.append(current_x)
return samples
# --- 4. 运行模拟并打印数据 ---
N = 100000
sigma_val = 0.8
print(f"--- 正在运行模拟 (N={N}) ---")
# 运行 A
samples_naive, walls = run_naive_metropolis(N, sigma_val)
print(f"\n[A. Naive Metropolis]")
print(f"❌ 撞墙次数: {walls}")
print(f"📉 算力浪费率: {walls/N*100:.2f}% (这些计算完全白费了)")
# 运行 B
samples_broken = run_broken_mh(N, sigma_val)
print(f"\n[B. Broken MH]")
print(f"✅ 撞墙次数: 0 (天生免疫)")
print(f"⚠️ 这里的平均值会偏大,因为没有修正项")
# 运行 C
samples_correct = run_correct_mh(N, sigma_val)
print(f"\n[C. Correct MH]")
print(f"✅ 撞墙次数: 0")
print(f"🎉 既不浪费算力,分布也是对的")
# --- 5. 绘图对比 ---
print("\n正在绘图...")
plt.figure(figsize=(16, 5))
x_true = np.linspace(0.1, 15, 1000)
y_true = target_pi(x_true)
y_true = y_true / np.trapz(y_true, x_true) # 归一化
# 图 1
plt.subplot(1, 3, 1)
plt.hist(samples_naive, bins=80, density=True, color='gray', alpha=0.6, label='Samples')
plt.plot(x_true, y_true, 'r-', lw=2, label='True Target')
plt.title(f"A. Naive (Symmetric)\nWasted {walls/N*100:.1f}% Calc")
plt.legend()
# 图 2
plt.subplot(1, 3, 2)
plt.hist(samples_broken, bins=80, density=True, color='orange', alpha=0.6, label='Biased Samples')
plt.plot(x_true, y_true, 'r-', lw=2, label='True Target')
plt.title("B. Broken MH (No Correction)\n⚠️ Curve Shifted Right!")
plt.legend()
# 图 3
plt.subplot(1, 3, 3)
plt.hist(samples_correct, bins=80, density=True, color='green', alpha=0.6, label='Correct Samples')
plt.plot(x_true, y_true, 'r-', lw=2, label='True Target')
plt.title("C. Correct MH (With Correction)\nPerfect Fit")
plt.legend()
plt.tight_layout()
plt.show()
--- 正在运行模拟 (N=100000) ---
[A. Naive Metropolis]
❌ 撞墙次数: 2606
📉 算力浪费率: 2.61% (这些计算完全白费了)
[B. Broken MH]
✅ 撞墙次数: 0 (天生免疫)
⚠️ 这里的平均值会偏大,因为没有修正项
[C. Correct MH]
✅ 撞墙次数: 0
🎉 既不浪费算力,分布也是对的
正在绘图...
/var/folders/mx/684cy0qs5zd3c_pdx4wy4pkc0000gn/T/ipykernel_28347/4241814712.py:99: DeprecationWarning: `trapz` is deprecated. Use `trapezoid` instead, or one of the numerical integration functions in `scipy.integrate`.
y_true = y_true / np.trapz(y_true, x_true) # 归一化
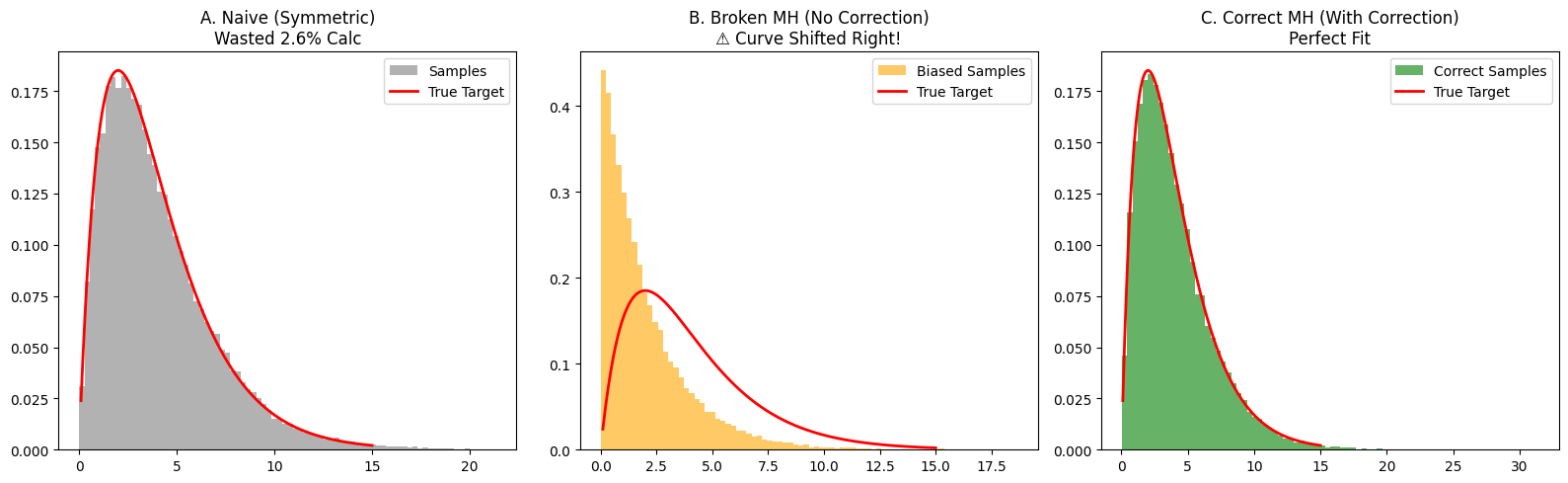
关于撞墙次数:
- Naive 方法在 $x$ 接近 0 的时候(比如 $x=0.5$),一半的提议都会跳到负数去。这些计算完全是无用功。
- 而 MH 方法利用 Log-Normal 提议,每次提议都是有效的正数。
正确性的验证 (Correctness)
- 图B:Broken MH (橙色)
- 直方图明显向左偏移(堆积在 0 附近),而红色理论曲线在右边。
- 数学解释
- 当你试图往右跳时 (x 变大,例如 1 -> 2):修正项 $= 2/1 = 2$ (大于 1)。
- 这意味着:修正项原本的作用是 “奖励” 往右跳的行为,增加接受率。
- Broken 算法删掉了这个奖励 $\to$导致往右跳变得比理论上更难 $\to$ 样本很难去右边。
- 当你试图往左跳时 (x 变小,例如 2 -> 1):修正项 $= 1/2 = 0.5$ (小于 1)。
- 这意味着:修正项原本的作用是**“惩罚”**往左跳的行为,降低接受率。
- Broken 算法删掉了这个惩罚 $\to$ 导致往左跳变得太容易了 $\to$ 样本更容易回到左边。
- 当你试图往右跳时 (x 变大,例如 1 -> 2):修正项 $= 2/1 = 2$ (大于 1)。
- 但加上修正项后,你可以看到绿色直方图(图C)完美地贴合了红色曲线。
- 这意味着:哈斯廷斯修正项成功地抵消了不对称提议带来的偏差!
MCMC 的诊断与调优 (Diagnostics & Tuning)
核心概念:三个体检指标
轨迹图 (Trace Plot) —— MCMC 的心电图
轨迹图的横轴是 迭代次数 (Time),纵轴是 采样值 (Value)。它记录了小人走的每一步。
- ✅ 好的轨迹(毛毛虫): 上下跳动非常剧烈,没有明显的趋势,看起来像一条毛茸茸的毛毛虫。这说明小人充分遍历了整个空间。
- ❌ 坏的轨迹(蛇): 缓慢地游走,或者长时间卡在一个地方不动。说明混合(Mixing)很差。
预热 (Burn-in) —— 丢弃垃圾时间
如果你把小人随机扔在了一个离山峰很远的地方(比如山峰在 0,你从 1000 开始跑)。小人需要花很多步才能从 1000 慢慢走到 0。这段“赶路”的时间,采样的并不是目标分布,而是过渡状态。
- 操作: 我们通常直接丢弃前 1000 或 5000 个样本,这一步叫 Burn-in。
接受率 (Acceptance Rate) —— 步长的金发姑娘原则
步长 $\sigma$ 决定了接受率:
- 太小(胆小鬼): 接受率 $\approx 99\%$。大家都在动,但走不远。轨迹图会像一条平滑的蛇。
- 太大(莽夫): 接受率 $\approx 1\%$。总是被拒绝。轨迹图会像方波(长时间平线,偶尔跳一下)。
- 完美(黄金区): 理论证明,对于高维高斯分布,最佳接受率在 23.4% 左右(一维可以在 40%-50%)。轨迹图是毛毛虫。
Python 代码实战:诊断“生病”的链
我们要模拟一个 标准正态分布(中心在 0),但我们将展示两种病态和一种健康的情况。
import numpy as np
import matplotlib.pyplot as plt
# 目标:标准正态分布
def target_pi(x):
return np.exp(-0.5 * x**2)
# 通用的 Metropolis 采样器
def run_metropolis(n_samples, start_x, sigma):
samples = []
current_x = start_x
accepted_count = 0
for _ in range(n_samples):
# 对称提议
proposal_x = np.random.normal(current_x, sigma)
# 计算接受率
alpha = min(1, target_pi(proposal_x) / target_pi(current_x))
if np.random.rand() < alpha:
current_x = proposal_x
accepted_count += 1
samples.append(current_x)
acc_rate = accepted_count / n_samples
return np.array(samples), acc_rate
# --- 实验设置 ---
N = 2000
start_bad = 20.0 # 离中心(0)很远,模拟初始化不当
start_good = 0.0
# 1. 病态 A: 步长太小 (胆小鬼) + 初始位置差
# sigma=0.1, start=20
samples_slow, acc_slow = run_metropolis(N, start_bad, sigma=0.1)
# 2. 病态 B: 步长太大 (莽夫)
# sigma=50, start=0
samples_stuck, acc_stuck = run_metropolis(N, start_good, sigma=50.0)
# 3. 健康 C: 步长适中 + 初始位置好
# sigma=1.0, start=0
samples_good, acc_good = run_metropolis(N, start_good, sigma=1.0)
# --- 绘图诊断 ---
plt.figure(figsize=(12, 10))
# 图 A: 步长太小 (Slow Mixing)
plt.subplot(3, 1, 1)
plt.plot(samples_slow, color='orange', lw=1)
plt.title(f"A. Step Size Too Small (Sigma=0.1) - Acc Rate: {acc_slow:.1%}")
plt.ylabel("Sample Value")
plt.axhline(0, color='r', linestyle='--', alpha=0.5, label="Target Mean (0)")
plt.axvline(750, color='k', linestyle=':', label="Burn-in Cutoff?")
plt.legend()
plt.text(100, 15, "Drifting slowly...", color='red', fontweight='bold')
# 图 B: 步长太大 (Stuck)
plt.subplot(3, 1, 2)
plt.plot(samples_stuck, color='purple', lw=1)
plt.title(f"B. Step Size Too Large (Sigma=50) - Acc Rate: {acc_stuck:.1%}")
plt.ylabel("Sample Value")
plt.axhline(0, color='r', linestyle='--', alpha=0.5, label="Target Mean (0)")
plt.text(100, 2, "Stuck (Flat lines)", color='red', fontweight='bold')
# 图 C: 健康 (Good Mixing)
plt.subplot(3, 1, 3)
plt.plot(samples_good, color='green', lw=1)
plt.title(f"C. Optimal Step Size (Sigma=1.0) - Acc Rate: {acc_good:.1%}")
plt.ylabel("Sample Value")
plt.xlabel("Iteration")
plt.axhline(0, color='r', linestyle='--', alpha=0.5, label="Target Mean (0)")
plt.text(100, 2, "Fuzzy Caterpillar (Healthy)", color='green', fontweight='bold')
plt.tight_layout()
plt.show()
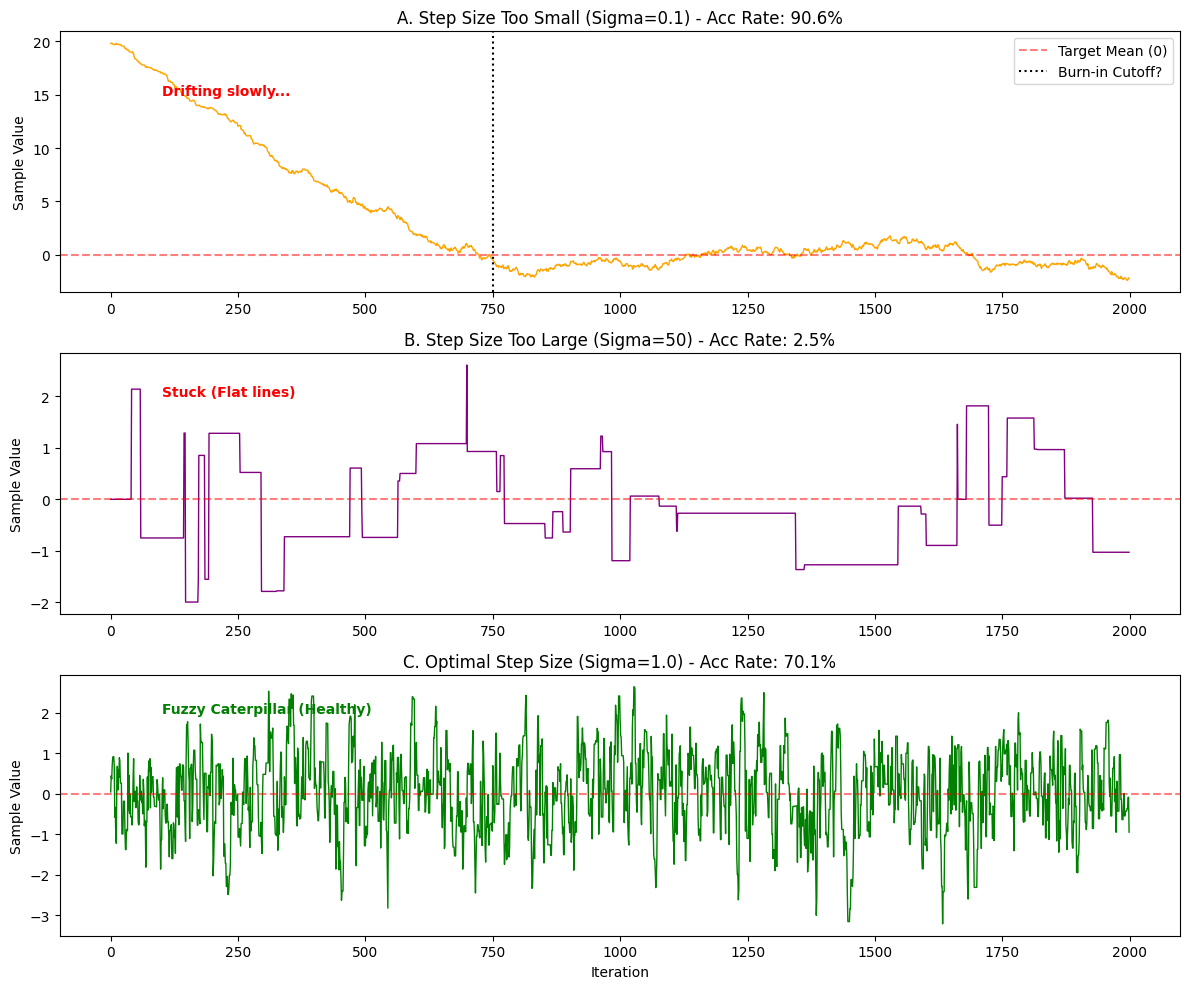
图 A:步长太小 (The Snake)
- 表现: 接受率极高(可能 >90%)。
- 轨迹形态: 线条虽然连续,但像蛇一样缓慢爬行。
- Burn-in 问题: 你会看到它从 20 开始,花了很久很久(可能 500-1000 步)才慢慢爬到 0 附近。
- 诊断: 这种链的相关性太强,收敛极慢。你需要增大步长,并且丢弃掉前面爬坡的数据 (Burn-in)。
图 B:步长太大 (The Square Wave)
- 表现: 接受率极低(可能 <5%)。
- 轨迹形态: 像方波或者楼梯。长时间是一条直线(一直被拒绝,值没变),突然跳一下,又是一条直线。
- 诊断: 这种链几乎没采到几个有效样本,效率极低。你需要减小步长。
图 C:健康 (The Caterpillar) 🐛
- 表现: 接受率适中(30% - 50%)。
- 轨迹形态: 毛茸茸的毛毛虫。你看不到明显的趋势,它围绕着中心 0 剧烈地震荡。
- 诊断: 这就是完美的 MCMC 链!这样的样本才是独立且有效的。
Scan to Share
微信扫一扫分享