我们要解决什么问题?(The Core Problem)
1. 核心困境:无法计算的 $Z$
在贝叶斯统计、物理模拟和高维计算中,我们经常需要从一个复杂的概率分布 $\pi(x)$ 中进行采样。但是,我们通常只知道这个分布的“形状”,却不知道它的“规模”。
- 已知: 未归一化的密度函数 $f(x)$(相对权重)。
- 未知: 归一化常数 $Z$(总和或积分)。$$\pi(x) = \frac{f(x)}{Z}, \quad \text{其中 } Z = \int f(x) dx$$
- 痛点: 在高维空间中,计算 $Z$(遍历整个空间求和)是计算上不可行的 (Intractable)。
- 后果: 因为不知道 $Z$,我们无法算出绝对概率 $\pi(x)$,传统的直接采样方法(如逆变换法)全部失效。
关于 $\pi$
| 场景 | $\pi$ 的形式 | 数学名称 | 物理意义 |
|---|---|---|---|
| 基础马尔可夫链 | 向量 | 平稳分布向量 | 各个状态的长期停留概率 |
| Metropolis (MCMC) | 函数 | 目标概率密度 | 我们希望采集样本的那个“形状” |
2. Metropolis 的解决策略:相对比值法
Metropolis 算法的核心洞见是:既然 $Z$ 算不出来,那就消掉它。
如果不去计算绝对概率,而是比较两个状态之间的相对概率比值,常数 $Z$ 就会在分子分母中自动抵消:
$$\frac{\pi(x_{\text{new}})}{\pi(x_{\text{old}})} = \frac{f(x_{\text{new}}) / Z}{f(x_{\text{old}}) / Z} = \frac{f(x_{\text{new}})}{f(x_{\text{old}})}$$这使得我们只利用相对高低($f(x)$的比值)就能判断两个状态的优劣,从而绕过了计算 $Z$ 的难题。
3. 连接点:为什么要用马尔可夫链?
既然我们只能做“局部比较”(比较当前位置和下一步位置),我们就无法一步到位地生成独立样本。我们需要一个能够在空间中游走的机制,这就引入了马尔可夫链。
动态模拟静态: 我们的目标是得到一个静态分布 $\pi$ 的样本,Metropolis 的手段是构造一个动态过程(马尔可夫链)。
逆向工程思维:
- 传统马尔可夫链问题: 给定转移矩阵 $P$ ,求稳态分布 $\pi$ 。
- Metropolis (MCMC) 问题: 已知目标分布 $\pi$ ,设计一个转移矩阵 $P$,使得这个链最终收敛到 $\pi$。
算法本质: Metropolis 算法通过细致平衡原则 (Detailed Balance) 构造了特殊的“接受/拒绝”规则,实时生成了一个HIA 链(齐次、不可约、非周期)。
最终结论: 根据遍历定理 (Ergodic Theorem),这个马尔可夫链跑出来的轨迹 (Trajectory),在长期统计上等价于从目标分布 $Z$ 中抽取的样本。
一句话总结: Metropolis 算法是为了解决 “在归一化常数 $Z$ 未知的情况下进行采样” 的难题,它通过 “构造一个以目标分布为稳态的马尔可夫链” 来实现这一目标。
Metropolis(随机游走)
为了保证收敛到 $\pi$,我们只需要构造一个满足 细致平衡方程 的链:
$$\pi_i P_{ij} = \pi_j P_{ji}$$Metropolis 算法把转移过程拆成了两步:
- 提议 (Proposal) $Q_{ij}$:提议转移方程。在数学符号里,它通常写作 $Q(x_{new} | x_{old})$ 或者 $q(x' | x)$。意思是:“已知我现在站在 $x_{old}$,我下一步提议跳到 $x_{new}$ 的概率是多少?”
- 请注意,它叫“提议” (Proposal)。因为它只是负责建议:“嘿,我们要不要试试去那里?” 至于到底去不去,那是后面 $\alpha$ (接受率) 决定的事。
- 在原始的 Metropolis 算法中,$Q$ 必须是对称的(Symmetry):$$Q(x_{new} | x_{old}) = Q(x_{old} | x_{new})$$
- 这样在后续计算接受率的时候,我们就可以把 $Q$ 消去了。
- 在实践时,$Q$ 通常就是一行简单的随机数生成代码。它有两种常见的形态
- A. 均匀游走 (Uniform Random Walk)
- 代码:
x_new = x_old + random.uniform(-1, 1) - 逻辑: 以当前位置为中心,画一个宽为 2 的盒子,盒子里的任何一个点被选中的概率都一样。
- 特点: 简单粗暴。
- 代码:
- B. 高斯游走 (Gaussian Random Walk)
- 代码:
x_new = x_old + random.normal(0, sigma) - 逻辑: 以当前位置为中心,生成一个正态分布。离当前位置越近的点,越容易被提议;太远的点很少被提议。
- 特点: 更符合自然界的移动规律(大多数时候迈小步,偶尔迈大步)。
- 代码:
- A. 均匀游走 (Uniform Random Walk)
- 接受 (Acceptance) $\alpha_{ij}$: 决定“我真的要跳过去吗,还是留在原地?”。
- 接受率虽然是由状态对 $(i, j)$ 决定的固定值,但在工程上,因为状态数量 $N$ 是天文数字,我们永远无法把这个 $N \times N$ 的表格预先算出来存储。我们只能 “走到哪,算到哪”。
- ⚠️ Metropolis 算法存在的全部意义,就是因为状态空间太大(或连续无限),导致我们无法提前确定这个关于接受率的“二维数组”。
所以,实际的转移概率是:$P_{ij} = Q_{ij} \times \alpha_{ij}$(注意这里 $i \ne j$)。把它代入细致平衡方程:
$$\pi_i (Q_{ij} \alpha_{ij}) = \pi_j (Q_{ji} \alpha_{ji})$$假设我们使用的是对称的提议规则(即 $Q_{ij} = Q_{ji}$,比如向左跳和向右跳的概率一样,都是 0.5)。那么方程就简化为:
$$\pi_i \alpha_{ij} = \pi_j \alpha_{ji}$$或者写成比率:
$$\frac{\alpha_{ij}}{\alpha_{ji}} = \frac{\pi_j}{\pi_i}$$三个版本的接受率 $\alpha_{ij}$
| 版本 | 公式核心 | 适用性 | 效率 (Peskun序) | 备注 |
|---|---|---|---|---|
| 1. Metropolis | $\frac{\pi_j}{\pi_i}$ | 仅对称 $q$ | ⭐⭐⭐ (最高) | 简单粗暴,只要能用就用它。 |
| 2. Barker | $\frac{\pi_j}{\pi_i + \pi_j}$ | 仅对称 $q$ | ⭐ (较低) | 物理学偏爱,数学性质好(光滑),但拒绝率高。 |
| 3. MH | $\frac{\pi_j q_{ji}}{\pi_i q_{ij}}$ | 任意 $q$ | ⭐⭐⭐ (最高) | 现代 MCMC 的基石,涵盖了第 1 种情况。 |
版本一:Metropolis 选择 (The Metropolis Choice)
假设你现在处于状态 $i$,系统建议你跳到状态 $j$。如果状态 $j$ 的概率比状态 $i$ 更高(即 $\pi_j > \pi_i$,这一步是往“高处”走),为了满足上面的比率,接受概率 $\alpha_{ij}$ 应该设为 1 (100%) 最合适(也最有效率)。因为既然 $\pi_j > \pi_i$,说明新状态 $j$ 是一个“更好”或者是“更重要”的状态,我们总是乐意往高处走,所以我们毫不犹豫地接受这个提议。
这得到了著名的 Metropolis 接受准则 (Acceptance Probability):
$$\alpha_{ij} = \min \left( 1, \frac{\pi_j}{\pi_i} \right)$$它包含了两种情况:
- 往高处走 ($\pi_j > \pi_i$): 比值 $>1$,取 $\min$ 后得到 1。总是接受。
- 往低处走 ($\pi_j < \pi_i$): 比值 $<1$,取 $\min$ 后得到 $\frac{\pi_j}{\pi_i}$。
- 这才是算法的灵魂!
- 即使新状态不如现在好,我们也有一定的概率(虽然不是 100%)接受它。
- 为什么? 为了防止陷入“局部最优” (Local Optima)。偶尔接受坏结果,能让你跳出小坑,去寻找更远处的最高峰。
🔍 适用条件:提议分布必须是对称的,即 $q_{ij} = q_{ji}$(从 $i$ 跳到 $j$ 的概率等于从 $j$ 跳回 $i$ 的概率)。
- 例子: 随机游走,向左一步和向右一步概率相等。
证明
$$ \pi_ip_{ij} = \pi_iq_{ij}\alpha_{ij} = \pi_iq_{ij}\min \left( 1, \frac{\pi_j}{\pi_i} \right) = q_{ij}\min \left( \pi_i, \pi_j \right) = q_{ij}\min \left( \pi_j, \pi_i \right) = \pi_jq_{ij}\min \left( 1, \frac{\pi_i}{\pi_j} \right) = \pi_jq_{ji}\min \left( 1, \frac{\pi_i}{\pi_j} \right) = \pi_jq_{ji} \alpha_{ji} $$优劣
- ✅ 优势(Peskun 定理): 这是数学上最优的选择。Peskun (1973) 证明了,在所有满足细致平衡的接受率函数中,Metropolis 选择能使得估计量的渐近方差最小。简单说:它最不爱拒绝人,能在保持平衡的前提下最大化流动性。
- ❌ 劣势:
- 受限。必须保证提议分布对称,无法处理非对称的复杂提议(如 Log-Normal)。
- 从计算机计算的角度来说,“对比操作”效率更低。
版本 二:Barker 选择 (The Barker Choice / Glauber Dynamics)
这个版本由 Barker (1965) 提出,在统计物理中(特别是 Ising 模型和自旋玻璃模拟)被称为 Glauber Dynamics 或 Heat Bath 的变体。
$$ \alpha_{ij} = \frac{\pi_i}{\pi_i+\pi_j} $$🔍 适用条件:同样通常用于 对称提议($q_{ij}=q_{ji}$) 的场景。常见于统计物理中的 Ising 模型 模拟(也称为 Heat Bath 算法的一种形式)。
证明
同样假设对称 $q$,只需证明 $\pi_i \alpha_{ij} = \pi_j \alpha_{ji}$。
- 左边 ($i \to j$):$$\pi_i \times \frac{\pi_j}{\pi_i + \pi_j} = \frac{\pi_i \pi_j}{\pi_i + \pi_j}$$
- 右边 ($j \to i$):$$\pi_j \times \frac{\pi_i}{\pi_j + \pi_i} = \frac{\pi_j \pi_i}{\pi_i + \pi_j}$$
- 结论: 分子分母完全一样。得证。
优劣
- ✅ 优势:函数光滑。$\min(1, x)$ 函数在 1 处有一个尖角(不可导),而 $\frac{x}{1+x}$ 是一条平滑的 Sigmoid 曲线。在某些需要对动力学过程求导的理论分析中,这个性质非常重要。
- ❌ 劣势: 效率较低。
- 当 $\pi_j > \pi_i$ 时,Metropolis 会 100% 接受。
- 但 Barker 即使面对更好的状态,接受率也永远小于 1(例如 $\pi_j = \pi_i$ 时,Metropolis 接受率是 1,Barker 只有 0.5)。这意味着它会拒绝更多的好样本,收敛变慢。
版本三:Metropolis-Hastings (MH) 接受率
$$ \alpha_{ij} = \min \left(1, \frac{q_{ji}\pi_j}{q_{ij}\pi_i}\right) $$🔍 适用条件:通用完全体。适用于任何提议分布 $q$,无论是否对称。它是第 1 种情况(版本一)的一般化形式。
数学证明
我们要证明完整形式:$\pi_i q_{ij} \alpha_{ij} = \pi_j q_{ji} \alpha_{ji}$。
定义接受率比值 $R = \frac{\pi_j q_{ji}}{\pi_i q_{ij}}$。不妨设 $R \ge 1$(即 $i \to j$ 是更有利或更倾向的流动方向):
- 左边 ($i \to j$): $\alpha_{ij} = \min(1, R) = 1$。$$\text{Left} = \pi_i q_{ij}$$
- 右边 ($j \to i$): 逆向的比值是 $1/R$,因为 $R \ge 1 \implies 1/R \le 1$,所以 $\alpha_{ji} = 1/R = \frac{\pi_i q_{ij}}{\pi_j q_{ji}}$。$$\text{Right} = \pi_j q_{ji} \times \left( \frac{\pi_i q_{ij}}{\pi_j q_{ji}} \right)$$消去 $\pi_j q_{ji}$ 后:$$\text{Right} = \pi_i q_{ij}$$
- 结论: 左边 = 右边。得证。
优劣
- ✅ 优势:极其灵活。因为引入了 $q_{ji}/q_{ij}$ 这个Hastings 修正项,你可以设计任何你喜欢的提议分布(比如 Log-Normal, MALA, 甚至神经网络生成的分布),只要能计算出概率密度即可。它解决了边界问题和高维引导问题。
- ❌ 劣势: 计算略繁琐。每次迭代都需要计算 $q$ 的比值。如果 $q$ 函数很复杂,计算成本会增加。
算法流程
离散 Metropolis 算法
- 定义与假设
- 状态空间 (State Space):$S = \{s_1, s_2, \dots, s_n\}$,是一个有限离散集合。
- 目标分布 (Target Distribution):$\pi = (\pi_1, \pi_2, \dots, \pi_n)$,满足 $\sum \pi_i = 1$。
- 这是一个极限稳定的分布。
- 提议矩阵 (Proposal Matrix):$Q = (q_{ij})$,其中 $q_{ij} = P(X^* = s_j | X_t = s_i)$。
- 对称性要求:$q_{ij} = q_{ji}, \forall i, j$。
- 当前状态:设 $X_t = s_i$。
- 转移算法步骤:在每一时刻 $t$,转移到 $t+1$ 的过程如下:
- 提议阶段 (Proposal Phase):
- 生成随机变量 $U_1 \sim \text{Uniform}(0, 1)$。
- 根据 $Q$ 矩阵的第 $i$ 行离散分布确定候选状态 $s_j$。具体地,找到 $j$ 使得:$$\sum_{k=1}^{j-1} q_{ik} \le U_1 < \sum_{k=1}^{j} q_{ik}$$
- 接受阶段 (Acceptance Phase):
- 计算接受概率 $\alpha_{ij} = \min \left( 1, \frac{\pi_j}{\pi_i} \right)$。
- 生成随机变量 $U_2 \sim \text{Uniform}(0, 1)$。
- 更新状态:$$X_{t+1} = \begin{cases} s_j & \text{若 } U_2 \le \alpha_{ij} \quad (\text{接受}) \\ s_i & \text{若 } U_2 > \alpha_{ij} \quad (\text{拒绝}) \end{cases}$$
- 注意,当 $\pi_j \lt \pi_i$ 时,$\alpha_{ij}=1$,这个时候总是接受的。
- 提议阶段 (Proposal Phase):
示例
设定场景
- 状态空间:$S = \{1, 2, 3\}$。
- 目标分布:$\pi = (0.2, 0.5, 0.3)$。
- 提议矩阵 $Q$(设定为一个对称的转移矩阵,每个状态有相等的概率跳向任意状态,包括自身):$$Q = \begin{pmatrix} 1/3 & 1/3 & 1/3 \\ 1/3 & 1/3 & 1/3 \\ 1/3 & 1/3 & 1/3 \end{pmatrix}$$
单步转移手算过程:
假设当前状态 $X_t = 1$。
- 第一步:生成提议状态
- 生成随机数 $U_1 = 0.72$。
- 查看 $Q$ 的第 1 行累积分布:$[0, 1/3, 2/3, 1]$。
- 由于 $2/3 \le 0.72 < 1$,落在第三个区间。
- 候选状态确定:$s_j = 3$。
- 第二步:计算接受率
- 我们要从状态 1 跳往状态 3。
- $\alpha_{13} = \min \left( 1, \frac{\pi_3}{\pi_1} \right) = \min \left( 1, \frac{0.3}{0.2} \right) = 1$。
- 第三步:决定最终状态
- 生成随机数 $U_2 = 0.45$。
- 由于 $U_2 \le \alpha_{13}$ (即 $0.45 \le 1$),接受提议。
- ⚠️ 事实上,这里因为 $\alpha_{13} == 1$,所以我们总是接受。
- 结果:$X_{t+1} = 3$。
再走一步:假设当前 $X_{t+1} = 3$
- 第一步:生成提议状态
- 生成随机数 $U_1 = 0.15$。查
- 看 $Q$ 的第 3 行累积分布:$[0, 1/3, 2/3, 1]$。
- 由于 $0 \le 0.15 < 1/3$,落在第一个区间。
- 候选状态确定:$s_j = 1$。
- 第二步:计算接受率
- 我们要从状态 3 跳往状态 1。
- $\alpha_{31} = \min \left( 1, \frac{\pi_1}{\pi_3} \right) = \min \left( 1, \frac{0.2}{0.3} \right) = 0.6667$。
- 第三步:决定最终状态
- 生成随机数 $U_2 = 0.82$。
- 由于 $U_2 > \alpha_{31}$ (即 $0.82 > 0.6667$),拒绝提议。
- 结果:$X_{t+2} = X_{t+1} = 3$。
import numpy as np
import matplotlib.pyplot as plt
# --- 1. 参数设置 ---
# 目标分布 pi (岛A: 0.2, 岛B: 0.5, 岛C: 0.3)
pi = np.array([0.2, 0.5, 0.3])
states_map = {0: 'Island A (0.2)', 1: 'Island B (0.5)', 2: 'Island C (0.3)'}
# 提议矩阵 Q (对称,均匀跳跃)
# Q[i][j] 代表从 i 提议去 j 的概率
Q = np.array([
[1/3, 1/3, 1/3],
[1/3, 1/3, 1/3],
[1/3, 1/3, 1/3]
])
def discrete_metropolis(n_iter, initial_state):
samples = []
current_state = initial_state
# 预计算 Q 的累积分布,用于 U1 的分位数查找
Q_cumsum = np.cumsum(Q, axis=1)
for t in range(n_iter):
# --- 第一步:生成提议 (U1) ---
u1 = np.random.uniform(0, 1)
# 根据 Q 的当前行累积概率确定候选状态 j
# 对应数学公式:sum(q_ik) < u1 <= sum(q_ik)
proposed_state = np.searchsorted(Q_cumsum[current_state], u1) # 逆变换采样 (Inverse Transform Sampling) 的离散实现
# --- 第二步:计算接受率 alpha ---
# 这里的 pi_j / pi_i
alpha = min(1, pi[proposed_state] / pi[current_state])
# --- 第三步:判定是否转移 (U2) ---
u2 = np.random.uniform(0, 1)
if u2 <= alpha:
# 接受提议
current_state = proposed_state
else:
# 拒绝提议,状态保持不变
pass
samples.append(current_state)
return np.array(samples)
# --- 2. 运行模拟 ---
N = 5000 # 迭代次数
samples = discrete_metropolis(N, initial_state=0)
# --- 3. 可视化展示 ---
plt.figure(figsize=(15, 10))
# 图 1: 轨迹图 (Trace Plot) - 只看前 100 步
# 这让我们看到具体的“跳跃”动作
plt.subplot(2, 2, 1)
plt.step(range(100), samples[:100], where='mid', color='blue', linewidth=1.5)
plt.yticks([0, 1, 2], [states_map[0], states_map[1], states_map[2]])
plt.title("1. Trace Plot (First 100 Steps)\nWatch the jumper move!", fontsize=12)
plt.grid(True, axis='y', linestyle='--', alpha=0.5)
plt.xlabel("Step")
# 图 2: 收敛图 (Convergence of Frequencies)
# 展示频率是如何随时间逼近真实概率的
plt.subplot(2, 2, 2)
# 计算动态频率
iterations = np.arange(1, N + 1)
prob_0 = np.cumsum(samples == 0) / iterations
prob_1 = np.cumsum(samples == 1) / iterations
prob_2 = np.cumsum(samples == 2) / iterations
plt.plot(prob_0, label='Simulated A', color='red', alpha=0.6)
plt.plot(prob_1, label='Simulated B', color='green', alpha=0.6)
plt.plot(prob_2, label='Simulated C', color='blue', alpha=0.6)
# 画出理论横线
plt.axhline(pi[0], color='red', linestyle='--', label='True A (0.2)')
plt.axhline(pi[1], color='green', linestyle='--', label='True B (0.5)')
plt.axhline(pi[2], color='blue', linestyle='--', label='True C (0.3)')
plt.title("2. Convergence Plot\nLaw of Large Numbers in action", fontsize=12)
plt.xlabel("Iterations")
plt.ylabel("Estimated Probability")
plt.legend()
plt.grid(True, alpha=0.3)
# 图 3: 最终直方图 vs 理论分布
plt.subplot(2, 1, 2)
counts = np.bincount(samples, minlength=3)
freqs = counts / N
x_pos = [0, 1, 2]
# 画柱状图
plt.bar(x_pos, freqs, width=0.4, label='Simulation', color='gray', alpha=0.7)
# 画理论点
plt.plot(x_pos, pi, 'ro', markersize=10, label='Theoretical Target', linestyle='None')
# 添加标签
for i, v in enumerate(freqs):
plt.text(i, v + 0.01, f"{v:.3f}", ha='center', fontweight='bold')
plt.xticks(x_pos, [states_map[0], states_map[1], states_map[2]])
plt.ylim(0, 0.6)
plt.title(f"3. Final Distribution (N={N})\nDid we match the target?", fontsize=12)
plt.legend()
plt.tight_layout()
plt.show()
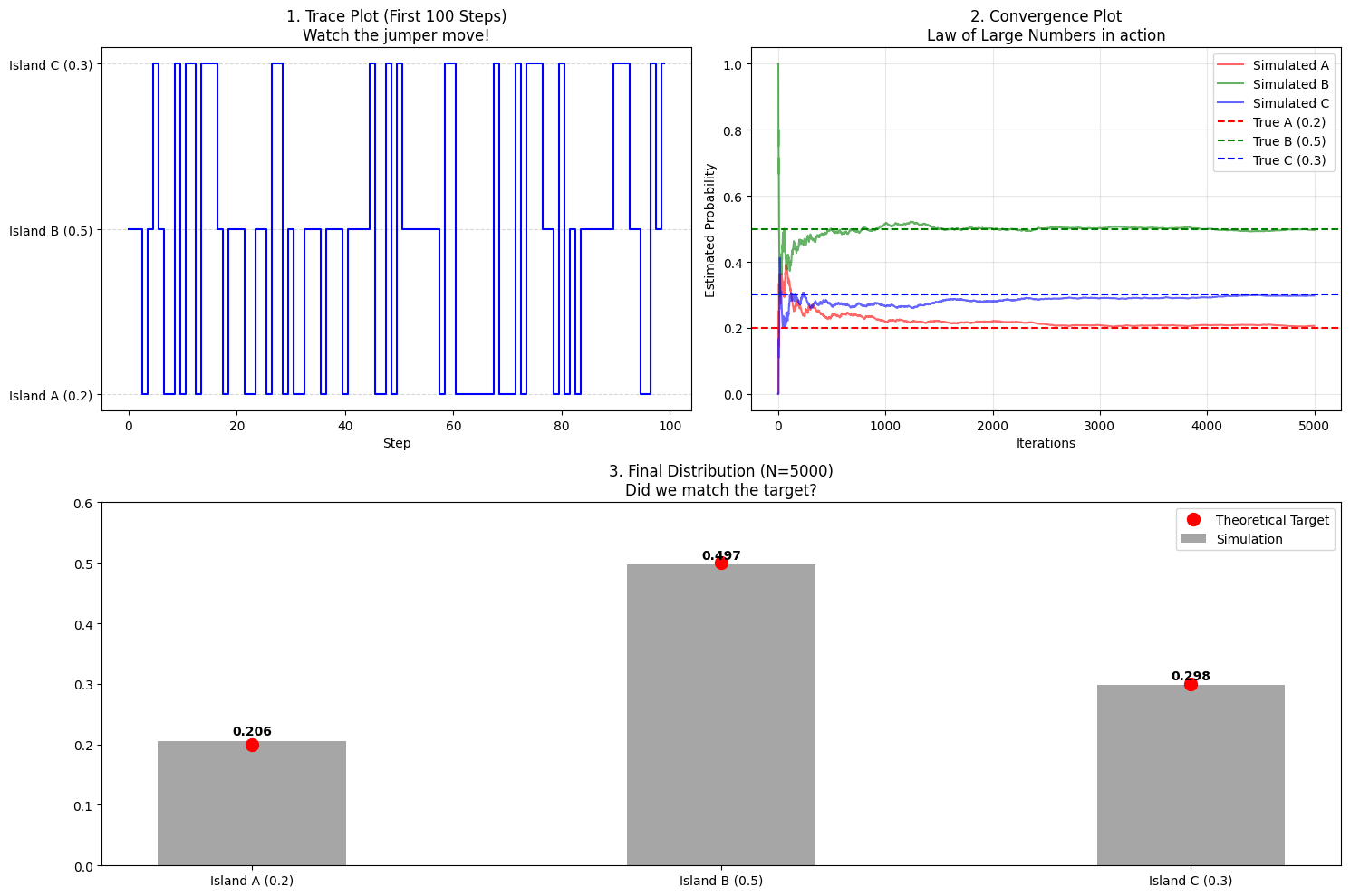
- 左上图:跳跃的细节 (Trace Plot)
- 这张图展示了算法的前 100 步。
- 直线部分: 你会看到有时候线条会在某一个水平高度(比如 Island B)保持好几步,形成一条横线。
- 数学含义: 这就是 拒绝 (Rejection)!
- 当小人在 B 岛,提议去 A 岛($0.2/0.5$ 只有 40% 概率接受)。
- 随机数 $U_2 > 0.4$,拒绝!小人留在 B。
- 关键点: 虽然位置没变,但在数学上,这算作“我们在 B 又采样了一次”。这正是为什么 B 的概率会比 A 高的原因——因为易进难出。
- 右上图:大数定律的魔法 (Convergence)
- 这张图展示了随着步数 $N$ 增加,每个岛的统计频率是如何变化的。
- 初期 (0-500步): 线条波动很大,很不稳定。
- 后期 (2000步以后): 线条逐渐变平,死死地贴在虚线(理论值)上。
- 数学含义: 这就是 遍历性 (Ergodicity)。只要时间足够长,访问频率一定收敛于 $\pi$。
- 下图:最终成绩单 (Comparison)
- 灰色的柱子是模拟出来的结果。
- 红色的圆点是定义的目标分布 $\pi$ 。
- 结果: 应该几乎完全重合。
连续 Metropolis 算法
定义与假设
- $q(x, y)$ 或者 $K(x, y)$ (提议核): 这是一个函数。
- 含义:给定当前位置 $x$,提议跳到 $y$ 的概率密度。它对标离散离散场景下的 $Q$,因为在连续空间中,状态是无限的,我们没法用矩阵来表示。
- 最著名的例子是 高斯核 (Gaussian Kernel):$$q(y|x) = \frac{1}{\sqrt{2\pi\sigma^2}} \exp\left( -\frac{(y-x)^2}{2\sigma^2} \right)$$
- 直观理解: 这就像以 $x$ 为中心的一个“钟形土包”。离 $x$ 越近的地方,被选为 $y$ 的概率越高。这其实就是我们之前说的 np.random.normal(x, sigma) 的数学本质。
- $\pi(x)$ (目标): 目标分布的概率密度函数 (PDF)。
算法步骤 (Algorithm Steps): 在时刻 $t$,当前状态为 $X_t = x$:
- 提议阶段 (Proposal):
- 从提议核 $q(\cdot | x)$ 中生成一个候选点 $x^*$。
- 代码实现:
x_star = x + np.random.normal(0, sigma)(如果用高斯核)。
- 接受阶段 (Acceptance):
- 计算接受率 (这里假设对称核 $q(x,y)=q(y,x)$,如高斯核):$$\alpha(x, x^*) = \min\left(1, \frac{\pi(x^*)}{\pi(x)}\right)$$
- 生成 $U \sim \text{Uniform}(0, 1)$。
- 决策阶段 (Update): $$ X_{t+1} = \begin{cases} x^* & \text{若 } U \le \alpha(x, x^*) \\ x & \text{若 } U \> \alpha(x, x^*) \end{cases} $$
示例
地形描述:有两座山峰。
- 主峰在 $x=2$。
- 次峰在 $x=-2$。
- 中间隔着深谷。
挑战:如果我们用的 Proposal Kernel (高斯核) 的方差 $\sigma$ 太小(步子太小),小人可能会被困在其中一座山头,跳不过峡谷(局部最优陷阱)。
import numpy as np
import matplotlib.pyplot as plt
# --- 1. 定义目标分布 (双峰) ---
# 这是一个非归一化的密度函数 (Unnormalized PDF)
# 峰 1: Mean=-2, Std=0.5
# 峰 2: Mean= 2, Std=0.5
def target_pdf(x):
p1 = np.exp(- (x + 2)**2 / (2 * 0.5**2))
p2 = np.exp(- (x - 2)**2 / (2 * 0.5**2))
return p1 + p2 # 双峰叠加
# --- 2. 定义提议核 (Proposal Kernel) ---
# 这里使用对称的高斯核: q(y|x) ~ N(x, sigma^2)
def sample_proposal_kernel(current_x, sigma):
return np.random.normal(current_x, sigma)
# --- 3. 连续 Metropolis 算法 ---
def continuous_metropolis(n_iter, start_x, sigma):
samples = []
current_x = start_x
accepted_count = 0
for _ in range(n_iter):
# A. 从核中采样 (Proposal)
x_star = sample_proposal_kernel(current_x, sigma)
# B. 计算接受率 (Symmetric Metropolis)
# alpha = min(1, pi(new) / pi(old))
p_new = target_pdf(x_star)
p_old = target_pdf(current_x)
alpha = min(1, p_new / p_old)
# C. 决策 (Decision)
u = np.random.uniform(0, 1)
if u <= alpha:
current_x = x_star
accepted_count += 1
samples.append(current_x)
return np.array(samples), accepted_count / n_iter
# --- 4. 运行模拟 ---
N = 10000
start_x = 0.0 # 从峡谷中间开始
# 实验 A: 窄核 (小步长) - 可能会被困住
samples_narrow, acc_narrow = continuous_metropolis(N, start_x, sigma=0.2)
# 实验 B: 宽核 (适中步长) - 能跨越峡谷
samples_wide, acc_wide = continuous_metropolis(N, start_x, sigma=1.5)
# --- 5. 可视化对比 ---
plt.figure(figsize=(14, 8))
x_axis = np.linspace(-6, 6, 1000)
y_truth = target_pdf(x_axis)
# 简单归一化一下用于画图对比
y_truth /= np.trapezoid(y_truth, x_axis)
# 图 1: 窄核 (Sigma=0.2)
plt.subplot(2, 2, 1)
plt.plot(samples_narrow, color='orange', alpha=0.7, lw=0.5)
plt.title(f"A. Narrow Kernel (sigma=0.2)\nAcc Rate: {acc_narrow:.1%}")
plt.ylabel("Position x")
plt.grid(alpha=0.3)
plt.subplot(2, 2, 3)
plt.hist(samples_narrow, bins=50, density=True, color='orange', alpha=0.5, label='Samples')
plt.plot(x_axis, y_truth, 'r-', lw=2, label='Target')
plt.title("Distribution (Trapped in one peak?)")
plt.legend()
# 图 2: 宽核 (Sigma=1.5)
plt.subplot(2, 2, 2)
plt.plot(samples_wide, color='green', alpha=0.7, lw=0.5)
plt.title(f"B. Wide Kernel (sigma=1.5)\nAcc Rate: {acc_wide:.1%}")
plt.ylabel("Position x")
plt.grid(alpha=0.3)
plt.subplot(2, 2, 4)
plt.hist(samples_wide, bins=50, density=True, color='green', alpha=0.5, label='Samples')
plt.plot(x_axis, y_truth, 'r-', lw=2, label='Target')
plt.title("Distribution (Good Mixing)")
plt.legend()
plt.tight_layout()
plt.show()
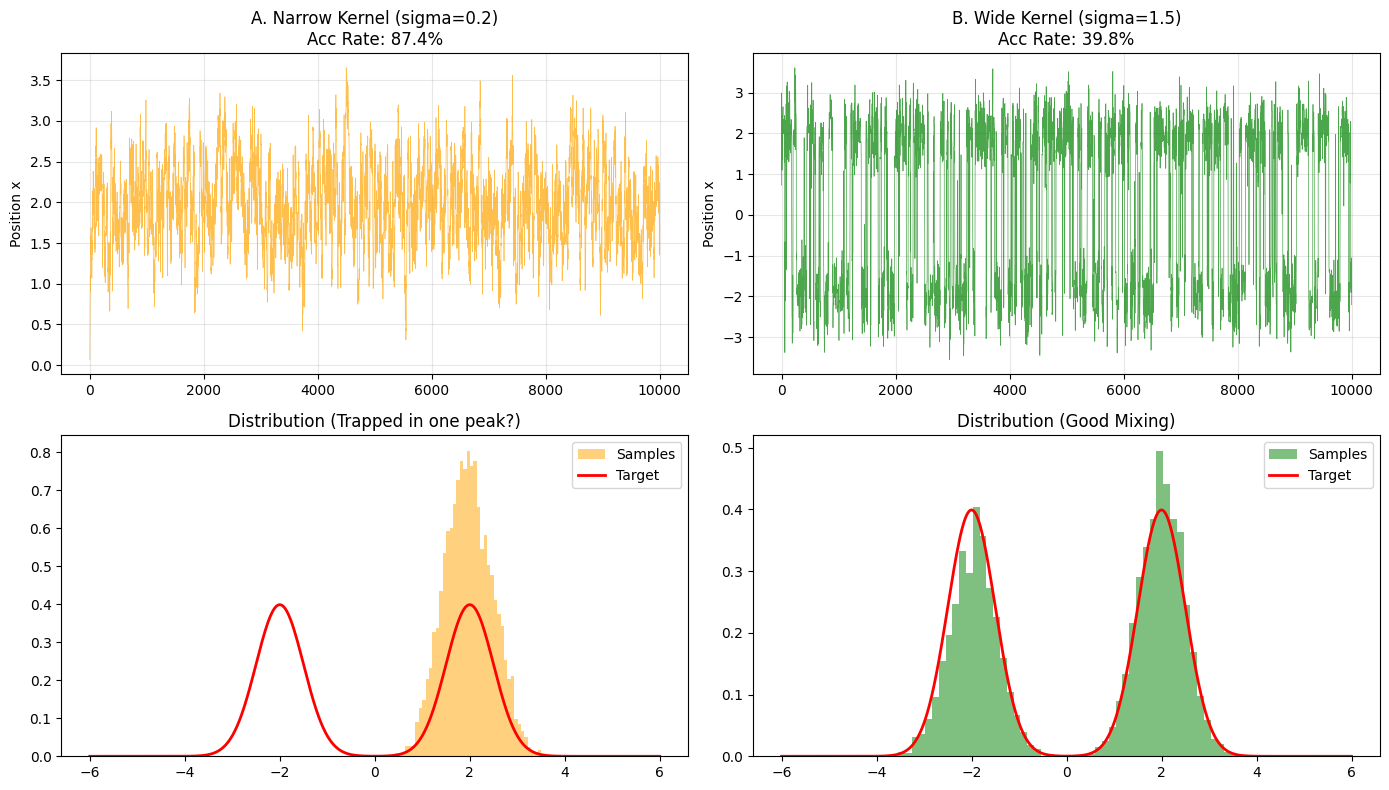
结果解析:
- 窄核 (Narrow Kernel, $\sigma=0.2$)
- 轨迹图 (左上): 你可能会看到小人一直待在 $x=0$ 附近,或者一旦滑入左边的山谷($x=-2$),就再也跳不到右边的山谷($x=2$)了。
- 分布图 (左下): 直方图可能只有单峰。
- 数学解释: 高斯核的尾巴太细了。要从 $-2$ 跳到 $2$,距离是 4。对于 $\sigma=0.2$ 的高斯分布来说,跳出 $4\sigma$ 以外的概率微乎其微。
- 宽核 (Wide Kernel, $\sigma=1.5$)
- 轨迹图 (右上): 你会看到小人在 $-2$ 和 $2$ 之间反复横跳。
- 分布图 (右下): 完美复现了双峰结构。
- 数学解释: 此时的高斯核足够宽,使得从一个山头“探”到另一个山头的概率变得可观,从而实现了全局遍历。
$Q$ 的选择
在 Metropolis 算法(对称提议)的框架下,选择 $Q$ 主要有三个维度的考量:尺度 (Scale)、形状 (Shape) 和 方向 (Orientation)。
尺度 (Scale):步子该迈多大?
这是最基础的问题,也就是在上一个代码中看到的 sigma。
- 过小 ($\sigma \ll$ 目标宽度):
- 现象:接受率极高(接近 100%),但轨迹像爬行的蜗牛。
- 术语:随机游走行为 (Random Walk Behavior)。
- 代价:你需要 $N^2$ 步才能走过距离 $N$。
- 过大 ($\sigma \gg$ 目标宽度):
- 现象:接受率极低(接近 0%),轨迹像心电图停搏。
- 原因:你总是试图从高概率区跳到极低概率区(荒野),然后被拒绝。
- 黄金标准 (Goldilocks Zone):
- 对于高维高斯目标分布,理论证明最佳接受率约为 23.4% ($0.234$)。
- 对于 1 维问题,通常在 40% ~ 50% 左右比较好。
- 💡 调参策略: 自适应 MCMC (Adaptive MCMC)。先跑一小段,如果接受率 $<10\%$,就把 $\sigma$ 减小;如果 $>60\%$,就把 $\sigma$ 增大。
形状 (Shape):尾巴该有多长?
默认我们都用 高斯分布 (Normal Distribution) 作为核,但它有一个致命弱点:轻尾 (Light-tailed)。
高斯分布的概率密度在远离中心时下降得极快(指数级下降)。这意味着它极度厌恶产生“大跳跃”。
- 场景:刚才的“双峰”问题。如果两座山峰隔得很远(比如距离 $10\sigma$),高斯核产生的提议几乎永远无法跨越这个峡谷。
- 解法:使用 柯西分布 (Cauchy Distribution) 或 t-分布。
- 在 python 中就是
np.random.standard_cauchy - 柯西分布的密度函数是 $\frac{1}{1+x^2}$(多项式级下降),它的尾巴非常“肥”。
- 效果:它大部分时候迈小步(局部搜索),但偶尔会发疯似地迈出巨大的一步(全局跳跃)。这对于跳出局部最优陷阱极其有效。
- 在 python 中就是
方向 (Orientation):如何穿越峡谷?
假设目标分布是一个细长的椭圆(两个变量高度相关),就像一条倾斜的峡谷。
- 这种分布的特点:
- 沿着峡谷方向(长轴):变化很慢,地势平坦。
- 垂直峡谷方向(短轴):变化极快,稍微偏一点就掉下悬崖(概率骤降)。
- 如果你用标准的高斯核 (各向同性, Isotropic):
- 你的 $Q$ 是一个正圆。
- 如果你把圆弄大(为了沿长轴走得快),你在短轴方向就会频繁撞墙(掉下悬崖),导致被拒绝。
- 如果你把圆弄小(为了在短轴方向安全),你在长轴方向就走不动了。
- 解法:预处理 (Preconditioning) 或 协方差矩阵 (Covariance Matrix)。
- 我们希望 $Q$ 的形状也是一个倾斜的椭圆,和目标分布的方向一致。
- 数学上,设目标协方差为 $\Sigma$,我们让提议分布为 $q(\cdot|x) \sim N(x, c^2 \Sigma)$。
- 这相当于先把坐标系旋转、缩放,把峡谷变成正圆,然后再采样。
收敛 (Convergence) 和 混合 (Mixing)
什么是 Mixing (混合)?
简单来说,Mixing 就是链条“忘掉”它从哪里出发、并完全融入目标分布的速度。
把它想象成往咖啡里倒牛奶:
- 刚开始 (未混合): 牛奶只在杯子的一角,浓度极不均匀(链条受初始值影响很大,还在赶路)。
- 搅拌中 (混合慢 - Slow Mixing): 你用很细的牙签慢慢划拉。牛奶在扩散,但很慢。你需要搅很久,杯子各处的牛奶浓度才一样。
- 搅拌好 (混合快 - Fast Mixing): 你用大勺子猛搅几下。牛奶瞬间均匀分布。此时你随便舀一勺,都代表了整杯咖啡的平均状态。
在 MCMC 中:
- Good Mixing: 无论你把小人扔在哪里,它能迅速跑遍整个地形(遍历性),且第 100 步的位置和第 1 步的位置几乎没有关系(独立性)。
- Bad Mixing: 小人要么被困在某个山头出不去(Stiff),要么走得太慢(Smooth),导致它采集的样本严重依赖于它刚才所在的位置。
衡量混合好坏的最佳标尺就是 自相关性 (Autocorrelation)。
核心度量工具:自相关函数 (ACF)
首先,我们要量化“当前这一步 $X_t$ 和它之前的某一步 $X_{t-k}$ 到底有多像”。这就是 Autocorrelation Function (ACF)。
- Lag $k$ (滞后):表示相隔 $k$ 步。
- $\rho_k$ (自相关系数):
- $\rho_k \approx 1$:强相关。今天的状态几乎完全由 $k$ 天前决定(坏事,说明没忘掉过去)。
- $\rho_k \approx 0$:无相关。今天的状态和 $k$ 天前无关(好事,说明是独立样本)。
我们在诊断时,会画一张 ACF 图:横轴是 $k$,纵轴是 $\rho_k$。我们希望 $\rho_k$ 像悬崖一样快速掉到 0。
场景 A: The Smooth Chain (平滑链 / 步长太小)
“Smooth $\to$ Long correlation”。
- 现象: 步长 $\sigma$ 很小,接受率极高($\approx 90\%$)。
- 轨迹图表现: 线条连续、圆滑,像一条蜿蜒的长蛇。
- 物理机制(随机游走):$$X_{t+1} = X_t + \epsilon \quad (\epsilon \text{ is tiny})$$虽然每一步都被接受了,但 $X_{t+1}$ 和 $X_t$ 长得几乎一模一样。
- Correlation 分析:
- 你要花 1000 步才能从分布的左边走到右边。
- 这意味着 $X_{1000}$ 依然能在某种程度上预测 $X_{1001}$。
- ACF 图: $\rho_k$ 下降极慢(Slow decay)。哪怕 $k=100$,相关性可能还有 0.8。结论:
- 混合极差 (Poor Mixing)。虽然在动,但动得太墨迹。
场景 B: The Stiff Chain (僵硬链 / 步长太大)
通常“步长极大”会导致接受率极低($\approx 1\%$)。
- 现象: 提议 $X_{new}$ 总是跳到很远的地方(概率极低区),然后被拒绝。
- 轨迹图表现: 方波 (Square Wave)。长时间是一条直线(僵硬、卡死),偶尔跳变一下。物理机制(拒绝即重复):$$X_{t+1} = X_t \quad (\text{因为拒绝})$$注意!当拒绝发生时,我们必须记录旧值。
- Correlation 分析:
- 你以为步子大,样本之间就没关系了吗?
- 错!因为大部分时间你都在 重复同一个数字。$X_t, X_{t+1}, \dots, X_{t+10}$ 全是同一个数值。这不仅仅是相关,这是完全相同!
- ACF 图: $\rho_k$ 依然很高,甚至比 Smooth 的情况更难看,因为它包含长段的 $1.0$ 相关性。
- 结论: 混合也极差。这种“僵硬”导致的短视(Short correlation)只存在于“提议”阶段,但在“接受”后的链条里,它是强相关的。
黄金平衡:有效样本量 (ESS)
既然“太顺滑”不行(相关性高),“太僵硬”也不行(重复率高,相关性也高)。我们要追求中间态。我们用一个核心指标来给链条打分:有效样本量 (Effective Sample Size, ESS)。
假设你跑了 $N = 10,000$ 步。
- 如果是 Smooth 链: 样本高度相关,这 1万个样本包含的信息量,可能只相当于 50 个 独立样本。
- 如果是 Stiff 链: 大部分样本是重复的,信息量可能只相当于 10 个 独立样本。
- 如果是 Optimal 链: 2-3 步就能忘掉过去,信息量可能相当于 3,000 个 独立样本。公式:$$N_{eff} = \frac{N}{1 + 2 \sum_{k=1}^{\infty} \rho_k}$$(分母就是 Integrated Autocorrelation Time, $\tau$,也就是“产生一个独立样本平均需要多少步”)
相关性的 U 型曲线
如果我们将 步长 (Step Size $\sigma$) 作为横轴,自相关时间 ($\tau$) 作为纵轴,会得到一条 U 型曲线。
- 左侧 (Small $\sigma$): Smooth。接受率高,但单步位移小。$\tau$ 很高(慢)。
- 右侧 (Large $\sigma$): Stiff。单步位移大,但接受率低(老是被拒,老是重复)。$\tau$ 很高(慢)。
- 谷底 (Optimal $\sigma$): Sweet Spot。
- 接受率控制在 23.4% (高维) 或 40-50% (1维)。
- ACF 像瀑布一样迅速掉到 0。
- 这就是所谓的 “Good Mixing”。
示例:三张 ACF 图
用 Python 模拟一个简单的 标准正态分布采样,并画出Smooth (步长小) vs Stiff (步长很大) vs Optimal (步长适中)的 轨迹图 (Trace Plot) 和 自相关图 (ACF Plot)。
import numpy as np
import matplotlib.pyplot as plt
import statsmodels.api as sm
# --- 1. 准备工作 ---
# 目标:标准正态分布 N(0, 1)
def target_log_prob(x):
return -0.5 * x**2
# Metropolis 采样核
def run_chain(n_steps, step_size, start_x=0.0):
samples = np.zeros(n_steps)
current_x = start_x
accepted = 0
for i in range(n_steps):
# 提议
proposal = current_x + np.random.normal(0, step_size)
# 接受率 (Log scale for stability)
log_alpha = target_log_prob(proposal) - target_log_prob(current_x)
# min(1, A) -> min(0, log_A) in log domain
if np.log(np.random.rand()) < log_alpha:
current_x = proposal
accepted += 1
samples[i] = current_x
acc_rate = accepted / n_steps
return samples, acc_rate
# --- 2. 运行三种场景 ---
N = 2000
# A. Smooth (步长太小)
chain_smooth, acc_smooth = run_chain(N, step_size=0.1)
# B. Stiff (步长太大)
chain_stiff, acc_stiff = run_chain(N, step_size=50.0)
# C. Optimal (步长适中)
chain_optimal, acc_optimal = run_chain(N, step_size=2.4) # 对于1维高斯,大一点没事
# --- 3. 绘图对比 (Trace + ACF) ---
fig, axes = plt.subplots(3, 2, figsize=(14, 10))
lags = 100 # 看前100步的相关性
# 辅助函数:画一行图
def plot_row(row_idx, samples, acc, title, color):
# 左边:Trace Plot
ax_trace = axes[row_idx, 0]
ax_trace.plot(samples, color=color, lw=1)
ax_trace.set_title(f"{title} - Trace (Acc: {acc:.1%})")
ax_trace.set_ylabel("Value")
# 右边:ACF Plot
ax_acf = axes[row_idx, 1]
# 使用 statsmodels 计算 ACF
acf_values = sm.tsa.acf(samples, nlags=lags)
ax_acf.bar(range(len(acf_values)), acf_values, width=0.3, color=color, alpha=0.7)
ax_acf.set_title(f"{title} - Autocorrelation")
ax_acf.set_ylim(-0.1, 1.1)
ax_acf.set_ylabel("Correlation")
ax_acf.axhline(0.05, linestyle='--', color='gray', alpha=0.5) # 显著性阈值
ax_acf.axhline(0, color='black', lw=1)
# 绘制三行
plot_row(0, chain_smooth, acc_smooth, "A. Smooth (Step=0.1)", "orange")
plot_row(1, chain_stiff, acc_stiff, "B. Stiff (Step=50)", "purple")
plot_row(2, chain_optimal, acc_optimal, "C. Optimal (Step=2.4)", "green")
plt.tight_layout()
plt.show()
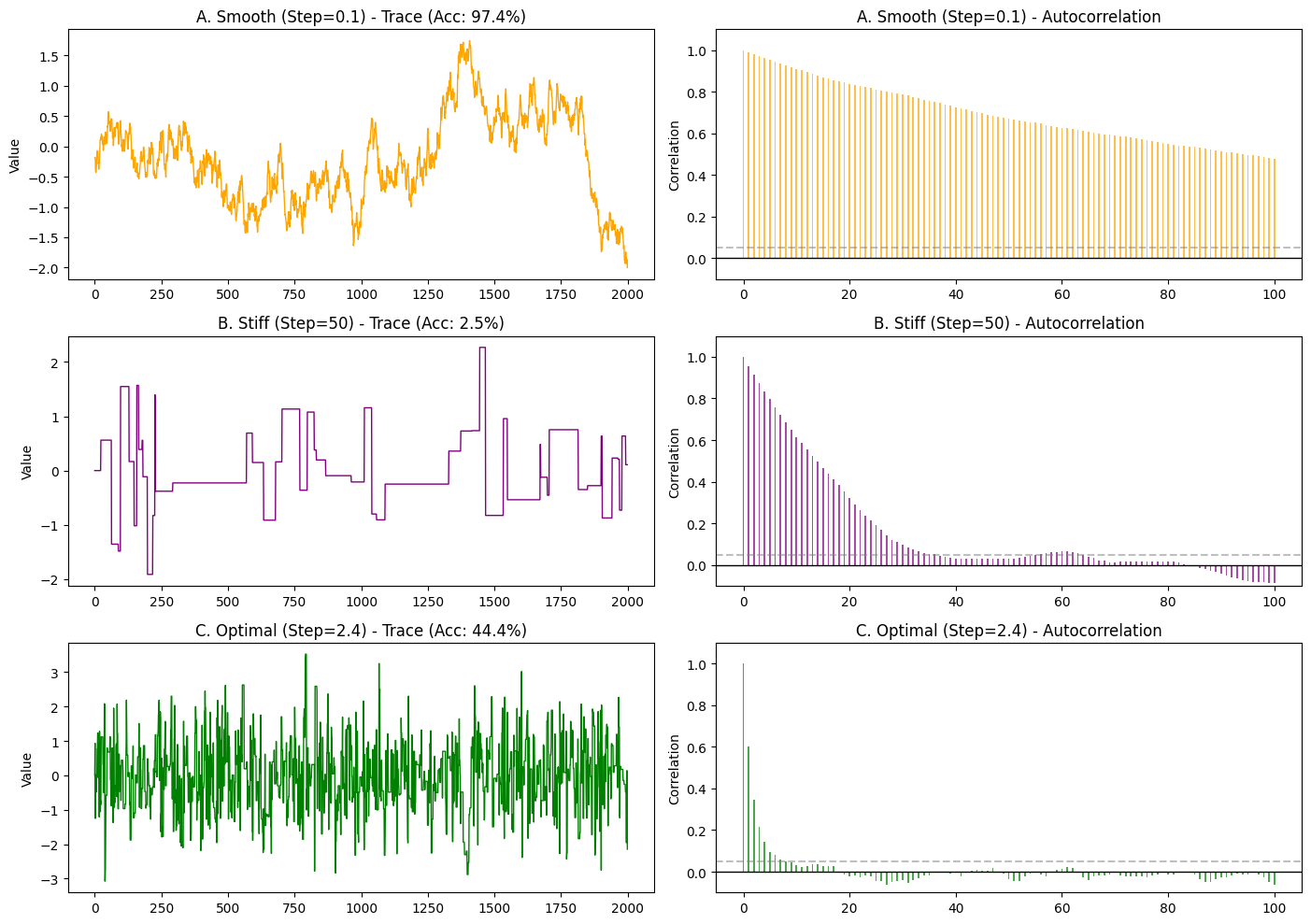
A. Smooth (橙色) —— 步长太小
- Trace (左): 像一条蜿蜒的蛇,爬得很慢。
- ACF (右): 长长的拖尾 (Slow Decay)。
- 即使到了 Lag=100(相隔100步),相关性可能还有 0.8 或 0.9。
- 含义: “我记得我祖宗十八代的样貌”。第 100 步的状态依然强烈依赖于第 1 步。这意味着虽然你跑了 2000 步,但有效样本量(独立样本)可能只有几十个。Mixing 很差。
B. Stiff (紫色) —— 步长太大
- Trace (左): 方波/心电图。长时间卡在一个值不动(拒绝),偶尔跳一下。
- ACF (右): 同样是长拖尾,甚至更严重。
- 你会发现相关性并不是像 Smooth 那样平滑下降,而是可能在一大段 Lag 内都维持在很高水平(因为数值根本没变,相关性当然是 1.0)。
- 含义: “我不仅记得过去,我简直就是过去的复制品”。由于大量重复值,信息量极低。Mixing 也很差。
C. Optimal (绿色) —— 黄金步长
- Trace (左): 毛毛虫。围绕 0 剧烈震荡,看不出趋势。
- ACF (右): 断崖式下跌 (Fast Decay)。
- Lag=0 时是 1.0(自己跟自己肯定相关)。
- Lag=5 或 10 左右,柱子就迅速掉到了 0 附近(虚线区域)。
- 含义: “好汉不提当年勇”。仅仅走了几步,链条就完全忘记了刚才在哪里。这说明每隔几步我们就能获得一个全新的、独立的有效样本。这就是 Perfect Mixing!
Burn-in(预热 / 老化)
Burn-in 指的是在 MCMC 采样开始后,我们要直接丢弃掉的前面 $N$ 个样本。
比如你让程序跑了 10,000 步,但你可能只保留第 1,001 步到第 10,000 步的数据。前 1,000 个样本就是 Burn-in 期,直接扔进垃圾桶。🗑️
为什么要扔掉它们?(The Bias Problem)
因为 MCMC 算法有一个 “初始化偏见” (Initialization Bias) 的问题。
想象你要统计一个万人体育馆里观众的平均身高:
- 随机空降: 你不可能直接空降到人最密集的地方。程序初始化时,通常是随机猜一个起点(比如 $x_0 = 100$)。
- 爬山赶路: 假设目标分布(大部分人)都在 $x=0$ 附近。你的采样器从小人从 $x=100$ 出发,它需要一步一步“爬”到 $x=0$ 的区域。
- 垃圾时间: 在它从 100 走到 0 的这段路程中,它记录的样本是:99, 98, …, 50, …, 10, …。
- 问题来了: 这些数值根本不属于目标分布($N(0,1)$)!它们只是小人“赶路”留下的脚印。
- 后果: 如果你把这些赶路的数据算进平均值,你的结果就会被严重拉高(偏离真实值)。
Burn-in 的作用就是: 等小人真正走到了体育馆中心(进入了平稳分布 Stationary Distribution),我们才开始按下录像键。之前的赶路过程统统剪掉。
Python 视觉实战:看见 Burn-in
模拟一个标准正态分布(中心在 0),但我们将起点故意设在极远的地方 ($x=20$),并且让步长稍微小一点(模拟走得慢的情况)。
import numpy as np
import matplotlib.pyplot as plt
# 1. 目标:标准正态分布 N(0, 1)
def target_log_prob(x):
return -0.5 * x**2
# 2. 模拟采样
def run_burnin_demo(n_steps, start_x, step_size):
samples = np.zeros(n_steps)
current_x = start_x
for i in range(n_steps):
# 提议
proposal = current_x + np.random.normal(0, step_size)
# 接受率
log_alpha = target_log_prob(proposal) - target_log_prob(current_x)
if np.log(np.random.rand()) < log_alpha:
current_x = proposal
samples[i] = current_x
return samples
# --- 设置 ---
N = 1000
start_val = 20.0 # <--- 起点离中心(0)非常远!
step = 0.5 # 步长较小,走得慢
chain = run_burnin_demo(N, start_val, step)
# --- 绘图 ---
plt.figure(figsize=(12, 6))
# 画出轨迹
plt.plot(chain, label='MCMC Chain', color='blue', lw=1.5)
# 标出 Burn-in 的分界线 (比如大约在第 200 步到达中心)
burn_in_cutoff = 200
plt.axvline(x=burn_in_cutoff, color='red', linestyle='--', lw=2, label='Burn-in Cutoff')
# 标注文字
plt.text(50, 15, "Transient Phase\n(Garbage Samples)", color='red', fontsize=12, fontweight='bold')
plt.text(400, 5, "Stationary Phase\n(Valid Samples)", color='green', fontsize=12, fontweight='bold')
plt.title(f"Visualizing Burn-in: Starting from x={start_val} to target N(0,1)")
plt.xlabel("Iteration")
plt.ylabel("Sample Value")
plt.axhline(0, color='gray', linestyle=':', alpha=0.5) # 目标均值
plt.legend()
plt.grid(True, alpha=0.3)
plt.show()
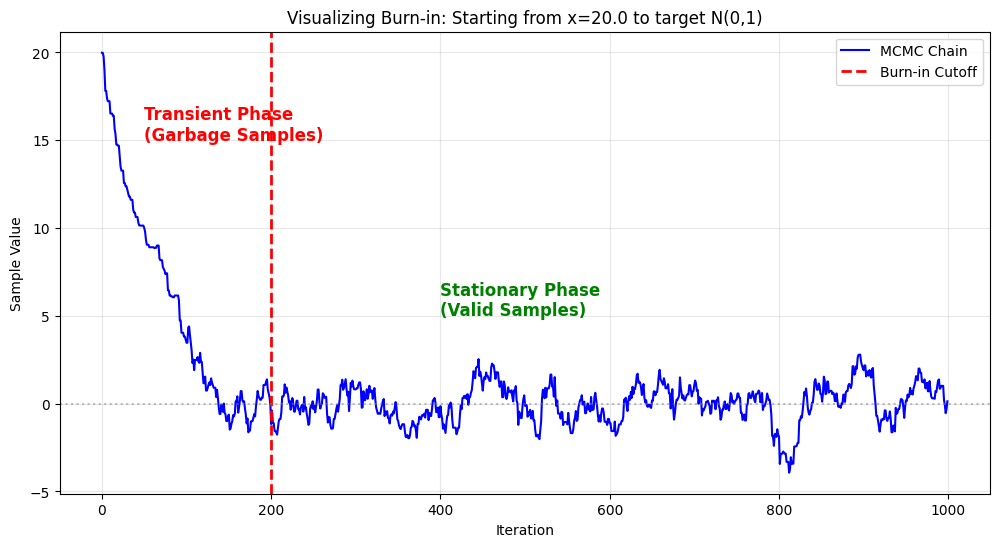
观察那条蓝线:
- 左侧(红线左边):
- 下坡路小人从 20 开始,一路跌跌撞撞往下掉。
- 这段时间的数据(比如 18, 15, 8…)全是垃圾。它们只反映了你的初始值设得有多偏,完全不代表 $N(0,1)$ 分布。
- 这就是 Burn-in Period。
- 右侧(红线右边):
- 毛毛虫大约在第 200 步左右,小人终于到达了 0 附近。
- 之后的轨迹开始围绕 0 上下震荡,看不出任何趋势。
- 这时候,链条才真正 **收敛(Converged)**到了目标分布。这之后的数据才是我们能用的。
Burn-in 要设多长?
这是 MCMC 调参中最玄学的问题之一。
- 看图法(最常用): 画出 Trace Plot(就像上面那样)。肉眼观察曲线什么时候不再有明显的上升或下降趋势,开始变得像毛毛虫一样平稳震荡。
- 保守法: 直接扔掉前 50% 的样本。反正现在的电脑算力便宜,多扔点不心疼,总比保留了垃圾数据强。
- 关联之前的知识:
- 如果步长太小(Smooth Chain),小人走得慢,从 20 走到 0 需要很久 $\to$ 需要很长的 Burn-in。
- 如果混合得好(Optimal Chain),小人几步就跳过去了 $\to$ 只需要很短的 Burn-in。
Scan to Share
微信扫一扫分享