MCs are in time, while MRFs are in space
从时间到空间——跨越维度的马尔可夫假设
在正式介绍马尔可夫随机场 (Markov Random Field, MRF) 之前,我们先回顾一下马尔可夫链 (Markov Chain)。
马尔可夫链的局限:时间的单向性
想象你正在记录每天的天气。在马尔可夫链的假设中,今天的天气 $x_n$ 只与昨天的天气 $x_{n-1}$ 有关,而与前天、大前天都无关 。用概率公式表达就是:
$$P(x_n | x_0, x_1, \dots, x_{n-1}) = P(x_n | x_{n-1})$$这种模型处理一维的、离散的 时间序列 (Time) 非常好用。但是,现实世界并不只有时间。如果我们面对的是一张二维的照片,或者一个三维的空间呢?这时候,只有前后关系的“链”就不够用了。毕竟,对于超过一维的情况,要如何定义前后关系呢?
引入网格 (Lattice) 与随机场 (Random Field)
为了解决二维或高维空间的问题,我们需要把一维的“线”扩展成二维的“网”——这就是 格点 (Lattice) 。
假设我们有一张由像素组成的黑白图片。图片的每一个像素点的位置可以用坐标 $m = (i, j)$ 来表示 。 在这个网格上的每一个点,我们都放置一个 随机变量 (Random Variables, RV),比如 $X_{i,j}$ 代表这个像素是黑还是白。
当这 $N \times M$ 个随机变量组合在一起时,它们就构成了一个 随机场 (Random Field) 。我们不仅关注某一个点,我们关注的是整个场里所有变量的 联合分布 (Joint Distribution):
$$P(X) = P(X_1, X_2, \dots, X_{NM})$$这就引出了 MRF 的核心难点:在一个拥有成千上万个像素的网格里,计算所有点的联合概率简直是天文数字。我们必须找到一种方法来简化它,这就是“马尔可夫性”要在这个空间里发挥的作用。
import numpy as np
import matplotlib.pyplot as plt
def create_random_field(rows, cols):
"""
创建一个简单的二维随机场 (Lattice)
这里我们假设每个格点 (随机变量) 只有两种状态:1 (黄) 或 -1 (紫)
"""
# 随机初始化 N x M 的网格,值在 {-1, 1} 之间
lattice = np.random.choice([-1, 1], size=(rows, cols))
return lattice
def plot_lattice(lattice, title="2D Random Field (Lattice)"):
"""
将网格可视化
"""
plt.figure(figsize=(6, 6))
# 使用 matshow 画出网格
plt.matshow(lattice, cmap='viridis', fignum=1)
# 画出网格线以便更清楚地看到 "格点" 的概念
rows, cols = lattice.shape
for i in range(rows):
plt.axhline(i - 0.5, color='white', linewidth=1)
for j in range(cols):
plt.axvline(j - 0.5, color='white', linewidth=1)
plt.title(title, pad=20)
plt.xticks([]) # 隐藏坐标轴数字
plt.yticks([])
plt.show()
# 1. 初始化一个 10x10 的随机场
N, M = 10, 10
my_field = create_random_field(N, M)
# 2. 可视化
plot_lattice(my_field, title="Initial Random Field (No Rules Applied)")

在上图中,你会看到一堆杂乱无章的色块。这是因为目前的随机场里,每个点都是完全独立的,没有任何规律。但在真实世界里(比如自然图像中),相邻的像素往往颜色是相近的。
这就引发了一个问题:我们该如何用数学语言,把“相邻的点互相影响”这个规则加入到这个场中呢?
建立社交网络——邻域(Neighbors)、马尔可夫性与“团”(Clique)
为了把马尔可夫链那优雅的“局部依赖”属性转移到这个空间场里,我们需要引入“距离”或者说“附近”的概念 。
1. 谁是我的邻居?(Neighbors)
在 MRF 中,我们用 $\Delta_m$ 来表示点 $m$ 的“邻域” (Neighborhood)
如何定义邻居呢?在图像处理或空间模型中,最常见的有两种:
- 4-邻域 (十字型):只看上下左右四个点 。
- 8-邻域 (九宫格):包括对角线上的点,一共八个 。
选择哪种邻域形状和大小,完全取决于你想要解决的具体问题 。但是,无论你怎么选,数学上必须严格遵守两个铁律 :
- 不包含自己:一个点不能是它自己的邻居 ($m \notin \Delta_m$) 。
- 绝对对称:如果 A 是 B 的邻居,那么 B 也必须是 A 的邻居 ($A \in \Delta_B \iff B \in \Delta_A$) 。
2. 空间的马尔可夫性 (Markov Property in MRF)
有了邻域,我们终于可以写出 MRF 最核心的数学定义了。
假设 $X_{-m}$ 代表网格上除了点 $m$ 以外的所有其他点。那么,空间马尔可夫性可以这样表达 :
$$P(X_m | X_{-m}) = P(X_m | X_{\Delta m})$$这句公式翻译成人话就是:
“如果你想预测点 $m$ 的状态,你不需要看整个宇宙(全图),你只需要看它周围的那几个邻居 ($\Delta_m$) 就足够了。”
这个伟大的等式,把一个全局的复杂计算,瞬间降维成了局部的简单计算!
3. 社交小团体:团 (Clique)
既然相邻的点会互相影响,我们需要一个基本的数学结构来量化这种影响。这里,就是“团 (Clique)”。
- 什么是团? 团是网格上的一个子集 (subset) 。在这个子集里,任何两个节点要么是同一个点,要么彼此之间互为邻居。简而言之,它必须根据你定义的邻域规则“连接”在一起 。
- 团的阶数 (Order): 团里面包含的节点数量,就是它的阶数。
- 一阶团 (Order 1):孤零零的一个点 。
- 二阶团 (Order 2):两个相邻的点连成的一条线 。
- (注:如果用 8-邻域,还会有三个点组成的三角形三阶团,等等。)
我们将为每一个“团”赋予一个 势能函数 (Clique Potential, $U_c$) 。比如,二阶团的势能 $U(X) = X_a X_b$ 可以用来评估相邻两个像素颜色是否一致。
物理直觉:什么是“势能”?
在物理学里,势能 (Energy/Potential) 越低,系统越稳定。
- 想象一个山坡上的石头:它在山顶时势能很高(不稳定,想滚下来);停在谷底时势能最低(最稳定,不想动了)。
- 在概率论里:系统越稳定,出现这种情况的概率就越大。
所以,在 MRF 里,我们设计“势能”的目的只有一个:给不同的状态打分。
- 低势能 = 这是一个好状态(符合常理,概率高)。
- 高势能 = 这是一个坏状态(反常,概率低)。
放到网格里:势能就是“惩罚/奖励规则”
势能函数 $U_c$ 就是我们为这个小团体量身定制的评分规则。
我们拿最经典的黑白图像去噪来举例。假设像素点的值只有两种:$+1$ (白) 和 $-1$ (黑)。
- 规则 A:一阶团势能 (Order 1)
- 一阶团就是孤零零的一个点 。它的势能 $U(X_a)$ 通常代表 “这个点本身长啥样”。
- 假设我们有一张带有噪点的观测图片 $Y$。如果当前估计的像素 $X_a$ 和实际观测到的像素 $Y_a$ 不一样,我们就惩罚它(势能变高)。
- 二阶团势能 (Order 2)
- 二阶团是两个相邻的点 $X_a$ 和 $X_b$ 。
- 在真实的图片中,相邻的两个像素大概率是同一个颜色(要么都是黑,要么都是白)。我们怎么用数学公式表达“鼓励同色,惩罚异色”呢?
- 为了让“好状态”势能低,我们稍微改写一下,加个负号定义为:$$U(X_a, X_b) = - X_a X_b$$
- 如果 $X_a$ 和 $X_b$ 颜色一样(都是 $+1$ 或都是 $-1$):$$X_a \cdot X_b = 1$$$$U = -1$$ (势能变低了!系统得到了奖励,变得更稳定)
- 如果 $X_a$ 和 $X_b$ 颜色不一样(一个是 $+1$,一个是 $-1$):$$X_a \cdot X_b = -1$$$$U = +1$$ (势能变高了!系统受到了惩罚,变得不稳定)
- 所以,势能函数 $U_c$ 其实就是一个“探测器”。它在网格上到处巡逻,每看到一对相邻的像素,就用 $X_a X_b$ 算一下。如果发现它们颜色不一样,就给总能量加上一点;如果颜色一样,就减去一点。
- 为了让“好状态”势能低,我们稍微改写一下,加个负号定义为:$$U(X_a, X_b) = - X_a X_b$$
所以,在 MRF 中,势能 $U_c$ 就是你人为设定的、用来描述局部节点之间“默契程度”的数学公式。
- 两个点越“违背常理”(比如本该一样的颜色却不一样),势能就越大。
- 两个点越“顺应常理”,势能就越小。
Python 直观示例
寻找邻域与构建“团”
为了在代码里落实马尔可夫性,我们需要写一个函数,专门用来找某个像素的“邻居”。
import numpy as np
import matplotlib.pyplot as plt
def get_neighbors(lattice, row, col, mode='4-way'):
"""
获取网格中指定位置 (row, col) 的邻居坐标
"""
rows, cols = lattice.shape
neighbors = []
# 4-邻域 (上下左右)
if mode == '4-way':
directions = [(-1, 0), (1, 0), (0, -1), (0, 1)] # 上下左右
# 8-邻域
elif mode == '8-way':
directions = [(-1, 0), (1, 0), (0, -1), (0, 1),
(-1, -1), (-1, 1), (1, -1), (1, 1)]
for dr, dc in directions:
r, c = row + dr, col + dc
# 边界检查:确保邻居没有跑出图像外
if 0 <= r < rows and 0 <= c < cols:
neighbors.append((r, c))
return neighbors
def plot_neighbors_and_cliques():
"""可视化邻域和二阶团"""
lattice = np.zeros((6, 6))
# 选定中心点 m
center_r, center_c = 2, 2
lattice[center_r, center_c] = 2 # 设为 2 (黄色代表中心点)
# 获取 4-邻域 的邻居
neighbors = get_neighbors(lattice, center_r, center_c, mode='4-way')
# 将邻居标记为 1 (绿色)
for r, c in neighbors:
lattice[r, c] = 1
plt.figure(figsize=(6, 6))
plt.matshow(lattice, cmap='viridis', fignum=1)
# 画网格线
rows, cols = lattice.shape
for i in range(rows): plt.axhline(i - 0.5, color='white', linewidth=2)
for j in range(cols): plt.axvline(j - 0.5, color='white', linewidth=2)
# 画出二阶团的连接线 (连结中心点和它的邻居)
for r, c in neighbors:
plt.plot([center_c, c], [center_r, r], color='red', linewidth=3, linestyle='--')
plt.title("Center Point (Yellow), 4-Neighbors (Green)\nRed lines represent 2nd-Order Cliques", pad=20)
plt.xticks([])
plt.yticks([])
plt.show()
# 运行可视化
plot_neighbors_and_cliques()
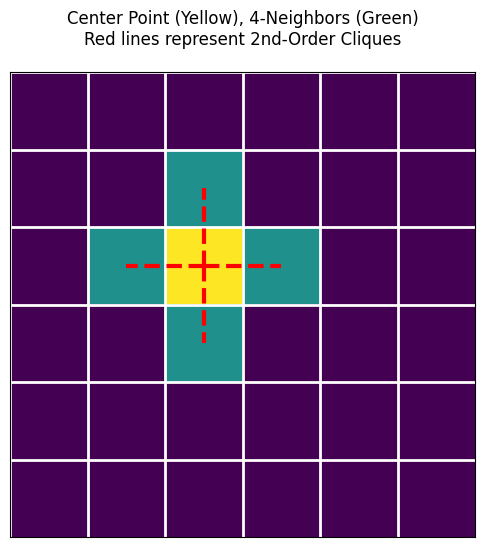
在上图中,你会看到红色的虚线把中心点和它的邻居连接了起来。每一根红色的连线和它两端的两个点,就构成了一个二阶团 (Clique)!
算算势能
# 假设这是两个相邻的像素点
x_a = 1 # 像素 A 是白色
x_b = -1 # 像素 B 是黑色
# 1. 定义我们设计的二阶团势能函数 U(x_a, x_b) = - x_a * x_b
def clique_potential_order2(pixel1, pixel2):
return - (pixel1 * pixel2)
# 2. 算一下它俩的势能
energy = clique_potential_order2(x_a, x_b)
print(f"像素A: {x_a}, 像素B: {x_b}")
print(f"这对相邻像素的势能是: {energy}")
# 结果会是 +1,因为它们颜色不同,系统很不开心(势能升高)。
像素A: 1, 像素B: -1
这对相邻像素的势能是: 1
现在,图纸已经画好了。但在自然界中,水往低处流,系统总是倾向于稳定。我们如何把这些局部的“团”组合起来,计算出整个随机场的能量呢?
从能量到概率——吉布斯分布与等价性定理
现在,我们知道了如何用“团势能” $U_c(x)$ 来给相邻像素的“默契程度”打分 。现在,我们把视野从局部放大到全局。
1. 全局的尺子:吉布斯能量 (Gibbs Energy)
如果把网格上所有可能的“团”(比如所有的单点、所有的相邻像素对)的势能全部加起来,我们就得到了整个系统(整张图像)的总能量,称为吉布斯能量 (Gibbs Energy) :
$$E(\underline{X}) = \sum_{c} U_c(\underline{X})$$- 物理直觉:如果整张图片非常平滑自然,大家都很“默契”,总能量 $E$ 就会很低;如果图片全是噪点,像雪花屏一样,总能量 $E$ 就会极高。
2. 从能量到概率:吉布斯分布 (Gibbs Distribution)
我们有了能量,但我们在统计学里最终需要的是概率。怎么把能量变成概率呢?统计物理学给了我们一个完美的公式——吉布斯分布 :
$$P(x) = A e^{-\lambda E(x)}$$- $E(x)$ 是我们刚算的吉布斯能量。
- $A$ 是一个归一化常数,为了确保所有可能状态的概率加起来等于 1,它的计算公式是 $A = \frac{1}{\int e^{-\lambda E(x)} dx}$ 。
- 负号的魔法:注意指数上的负号。能量 $E(x)$ 越低,$-E(x)$ 就越大,算出来的概率 $P(x)$ 就越高!这完美契合了“水往低处流,系统越稳定(能量低)越容易出现”的自然法则。
3. MRF 皇冠上的明珠:Hammersley-Clifford 定理
此时,你可能会问:这和我们第一节说的“马尔可夫随机场 (MRF)”有什么关系?
这就引出了概率图模型中最伟大的定理之一:
如果一个随机场的概率分布是吉布斯分布,那么它必然是一个马尔可夫随机场 (MRF),反之亦然 。
简写为:
$$MRF \iff Gibbs$$为什么这个定理这么牛?
因为定义一个宏观的、包含上万个节点的联合概率分布 是根本不可能完成的任务。但这个定理告诉我们:你不需要去算那个天文数字的联合概率!你只需要在微观上定义好每个小团体(团)的势能规则 $U_c(x)$,然后把它们加起来,你自然就得到了一个满足马尔可夫性质的完美场!
4. 见证奇迹的时刻:推导证明 (The Proof)
我们要证明:在一个服从吉布斯分布的网格中,某个点 $m$ 的状态只和它的邻居有关(即满足马尔可夫性 $P(X_m | X_{-m}) = P(X_m | X_{\Delta m})$)。
第一步:写出条件概率
根据基础的条件概率公式 $P(A|B) = \frac{P(AB)}{P(B)}$ ,我们可以写出点 $m$ 的条件概率:
$$P(X_m | X_{-m}) = \frac{P(X_m, X_{-m})}{P(X_{-m})} = \frac{P(X)}{\sum_{X_m} P(X)}$$第二步:代入吉布斯分布
把 $P(X) = A e^{-\lambda E(X)}$ 代入上面的公式中,常数 $A$ 在分子分母中直接约掉了 :
$$= \frac{e^{-\lambda E(\underline{x})}}{\sum_{X_m} e^{-\lambda E(\underline{x})}}$$第三步:拆分能量
我们知道总能量 $E(X) = \sum_c U_c(X)$ 。 网格上成千上万个团,我们可以把它们强行分成两类:
- 包含点 $m$ 的团:$\sum_{m \in c} U_c(X)$
- 不包含点 $m$ 的团:$\sum_{m \notin c} U_c(X)$
把这两部分代回指数中,利用 $e^{a+b} = e^a \cdot e^b$ :
$$= \frac{e^{-\lambda \sum_{m \in c} U_c(x)} \cdot e^{-\lambda \sum_{m \notin c} U_c(x)}}{\sum_{X_m} \left[ e^{-\lambda \sum_{m \in c} U_c(x)} \cdot e^{-\lambda \sum_{m \notin c} U_c(x)} \right]}$$第四步:完美的抵消 (Cancellation)
注意分母是在对 $X_m$ 求和。对于那些不包含点 $m$ 的团($\sum_{m \notin c} U_c(x)$),它们的值和 $X_m$ 取什么完全没关系!
所以在对 $X_m$ 求和时,这一项就相当于一个常数,可以直接提取到求和符号外面。
提取出来后,它和分子中一模一样的项完美抵消了!最后只剩下包含点 $m$ 的团 :
$$= \frac{e^{-\lambda \sum_{m \in c} U_c(x)}}{\sum_{X_m} e^{-\lambda \sum_{m \in c} U_c(x)}}$$结论:
你看最后剩下的这个式子,所有的计算都只依赖于“包含点 $m$ 的团”。而根据“团”的定义,包含点 $m$ 的团里,除了 $m$ 本身,就只有 $m$ 的邻居 $\Delta_m$ 了! 这完美地证明了:
$$P(X_m | X_{-m}) = P(X_m | X_{\Delta m})$$Python 直观示例:能量算概率
我们可以写一个简单的函数,直观地感受一下能量 $E$ 是如何通过吉布斯公式变成概率 $P$ 的。
import numpy as np
import matplotlib.pyplot as plt
def gibbs_probability(energies, lambda_param=1.0):
"""
将一组能量值转换为吉布斯概率分布
P(x) \\propto e^{-\\lambda E(x)}
"""
# 计算未归一化的权重 e^{-\lambda E(x)}
weights = np.exp(-lambda_param * np.array(energies))
# 归一化 (除以总和 A),使得概率加起来等于 1
probabilities = weights / np.sum(weights)
return probabilities
# 假设我们有三个状态,计算出了它们的总能量
# 状态 A: 能量极低 (非常稳定)
# 状态 B: 能量中等
# 状态 C: 能量极高 (非常反常)
energy_states = [1.5, 5.0, 12.0]
state_names = ['State A (Low E)', 'State B (Med E)', 'State C (High E)']
# 计算概率
probs = gibbs_probability(energy_states, lambda_param=1.0)
# 打印结果
for name, e, p in zip(state_names, energy_states, probs):
print(f"{name}: Energy = {e:5.1f} --> Probability = {p*100:6.2f}%")
# 可视化
plt.figure(figsize=(8, 4))
plt.bar(state_names, probs, color=['green', 'orange', 'red'])
plt.title("Gibbs Distribution: Lower Energy = Higher Probability")
plt.ylabel("Probability")
plt.show()
State A (Low E): Energy = 1.5 --> Probability = 97.07%
State B (Med E): Energy = 5.0 --> Probability = 2.93%
State C (High E): Energy = 12.0 --> Probability = 0.00%
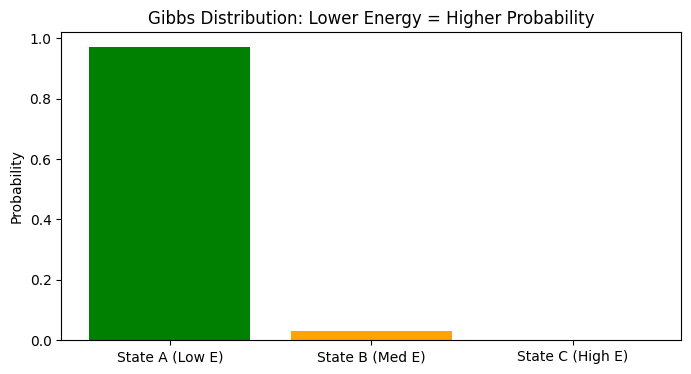
通过上面代码你会发现,能量低的状态 A 占据了几乎所有的概率(97%),而能量高的状态 C 出现的概率几乎为 0。
现在,我们有了理论武器(MRF 和 Gibbs 的等价性),也知道了如何算概率。那么,面对一张充满噪点的烂图,我们如何让计算机自动去寻找那个“能量最低、概率最大”的完美状态呢?
寻找最优解——模拟退火与 Gibbs 采样大显身手
graph TD;
A["开始: 输入带噪图像 Y"] --> B["建模与初始化<br>设定 X=Y, T_init, T_end"]
subgraph S1 ["外层循环: 模拟退火 (Simulated Annealing)"]
B --> C{"当前温度 T > T_end ?"}
C -- 是 --> D["计算当前温度 T"]
subgraph S2 ["内层循环: Gibbs 采样 (Gibbs Sampler)"]
D --> E["选择下一个像素点 m"]
E --> F["计算点 m 变成 +1 时的局部能量 E_pos"]
F --> G["计算点 m 变成 -1 时的局部能量 E_neg"]
G --> H["计算吉布斯概率<br>P(+1) = 1 / (1 + exp(ΔE/T))"]
H --> I{"生成随机数 u < P(+1) ?"}
I -- "是 (接受+1)" --> J["点 m 设为 +1"]
I -- "否 (接受-1)" --> K["点 m 设为 -1"]
J --> L{"遍历完所有像素了吗?"}
K --> L
L -- 否 --> E
end
L -- 是 --> M["完成一次全图扫描, 降温"]
M --> C
end
C -- "否 (温度已极低)" --> N["算法收敛: 冻结当前状态"]
N --> O["结束: 输出去噪后的图像 X"]
%% 样式设置
style A fill:#f9f,stroke:#333,stroke-width:2px
style O fill:#f9f,stroke:#333,stroke-width:2px
style B fill:#bbf,stroke:#f66,stroke-width:2px,color:#fff,stroke-dasharray:5
我们现在知道了吉布斯分布的核心逻辑:要想让系统处于概率最大的完美状态,就必须让系统的总能量降到最低。
在 MRF 的实际应用中(比如图像去噪、图像分割),我们的总体工作流 (Overall Workflow) 非常明确 :
- 建模 (Model a MRF):把问题变成一个 MRF 网格,定义好势能规则 。
- 优化 (Optimization):寻找拥有最高条件概率(最低能量)的那个状态 。
- 求解:利用模拟退火算法,配合降温法则和 Gibbs 采样技术来实现多维度的状态更新 。
这套求解方案中有两位关键的“超级英雄”:
1. 局部探路者:Gibbs 采样 (Gibbs Sampler)
在有成千上万个变量的 N 维空间里,同时更新所有变量是会“爆炸”的 。Gibbs 采样的聪明之处在于:每次只盯着一个点 看,其他点全部当成木头人(固定不动)。
- 如何更新这个点? 这正是 MRF 最耀眼的时刻!根据我们在上一节证明的马尔可夫性,我们完全不需要理会全图,我们只需要利用马尔可夫属性 (exploiting the Markov property),看看这个点周围的几个邻居就行了 。
- 计算概率:算一下这个点变成黑色时,它和邻居组成的局部能量是多少;变成白色时,局部能量又是多少。然后用吉布斯公式把能量转化为概率,掷个骰子(采样)决定它的新颜色。
2. 全局指挥官:模拟退火 (Simulated Annealing)
如果只用 Gibbs 采样,算法很容易卡在一个“还不错但不是最好”的局部死胡同里。为了找到全局绝对的最优解,我们需要引入温度 (Temperature) 的概念。
整个退火过程分为以下几步 :
- 高温探索 (Initial: Fix a high Temp $T_0$):一开始设定一个很高的温度 $T_0$ 。此时吉布斯分布非常平缓,算法像一个无头苍蝇,可以轻易接受“变差”的结果。这有助于它跳出局部的坑 。
- 逐步降温 (Decrease T):让温度慢慢降下来 ($T_0 > T_1 > T_2 > \dots > T_n$) 。随着温度降低,系统越来越挑剔,只倾向于接受“让能量变低”的改变。
- 降温法则 (Temperature Law):在纯理论中,Geman & Geman 证明了如果按照 $T(t) \sim \log(1/t + 1)$ 的对数规律极慢地降温,必定能找到全局最优解 。但在工程代码里,为了速度,我们通常会用几何降温法(每次乘以 0.99)。
- 得出结果:在最低温 $T_n$ 下,系统会被“冻结”在能量最低的那个最优解里 。我们把最后采样的结果取个平均值 (mean),这就是我们要找的最终答案。
Python 实战:用 MRF 和模拟退火给图像去噪
我们来写一段不到 100 行的代码来感受这一过程。我们将人为制造一张布满噪点的图像,然后利用 MRF + Gibbs 采样 + 模拟退火,让计算机自己把它“洗干净”!
这个模型在学术界有一个赫赫有名的名字:Ising Model (伊辛模型)。
import numpy as np
import matplotlib.pyplot as plt
def add_noise(image, noise_ratio=0.2):
"""给干净的二值图像添加噪点"""
noisy_img = np.copy(image)
# 随机生成噪点掩码
mask = np.random.rand(*image.shape) < noise_ratio
noisy_img[mask] = -noisy_img[mask] # 翻转颜色 (1变-1, -1变1)
return noisy_img
def get_local_energy(padded_X, Y, r, c, weight_data, weight_smooth):
"""
计算局部吉布斯能量 (对应一阶团和二阶团)
padded_X: 当前状态的图像 (加了 padding 方便处理边界)
Y: 观测到的带噪图像
r, c: 当前像素在 padded_X 中的坐标
"""
# 当前像素的状态 x_m
x_m = padded_X[r, c]
# 1. 一阶团势能 (Data Term): 惩罚和观测图像 Y 不同的情况
# 注意:Y 没有 padding,所以坐标是 [r-1, c-1]
# 如果 x_m 和 Y 相同,x_m * Y = 1,加上负号变成 -1 (能量低,系统得到奖励)
energy_data = - weight_data * (x_m * Y[r-1, c-1])
# 2. 二阶团势能 (Smoothness Term): 惩罚和四个邻居不同的情况
# 获取上下左右四个邻居的值
neighbors_sum = (padded_X[r-1, c] + padded_X[r+1, c] +
padded_X[r, c-1] + padded_X[r, c+1])
# 如果 x_m 和大多数邻居同色,乘积大于 0,加上负号变负数 (能量低,系统得到奖励)
energy_smooth = - weight_smooth * (x_m * neighbors_sum)
return energy_data + energy_smooth
def mrf_denoising(Y, iter_max=15, T_init=5.0, T_end=0.1):
"""MRF 图像去噪 (使用 Gibbs 采样和模拟退火)"""
rows, cols = Y.shape
X = np.copy(Y) # 初始状态从带噪图像开始
# 几何降温的系数 tau
tau = -np.log(T_end / T_init) / (iter_max - 1)
for i in range(iter_max):
T_curr = T_init * np.exp(-tau * i) # 计算当前温度
# 为了方便处理边界,给图像加一圈 0 (padding)
padded_X = np.pad(X, 1, mode='constant')
# Gibbs 采样:逐个像素更新 (利用马尔可夫性,只看邻居)
for r in range(1, rows + 1):
for c in range(1, cols + 1):
# --- 修正的地方在这里:参数名统一为 weight_data 和 weight_smooth ---
# 假设当前像素变成 1 的能量
padded_X[r, c] = 1
E_pos = get_local_energy(padded_X, Y, r, c, weight_data=1.0, weight_smooth=1.5)
# 假设当前像素变成 -1 的能量
padded_X[r, c] = -1
E_neg = get_local_energy(padded_X, Y, r, c, weight_data=1.0, weight_smooth=1.5)
# 吉布斯公式算概率: P(x=1) = exp(-E_pos/T) / (exp(-E_pos/T) + exp(-E_neg/T))
# 为防止计算溢出,化简为 logistic 形式: 1 / (1 + exp((E_pos - E_neg) / T))
delta_E = E_pos - E_neg
prob_pos = 1.0 / (1.0 + np.exp(delta_E / T_curr))
# 掷骰子采样!生成一个 0~1 的随机数
if np.random.rand() < prob_pos:
padded_X[r, c] = 1
else:
padded_X[r, c] = -1
# 剥去 padding,更新整张图,为下一次迭代准备
X = padded_X[1:-1, 1:-1]
print(f"Iteration {i+1:2d}/{iter_max}, Temp = {T_curr:.2f}")
return X
# ----------------- 运行与可视化 -----------------
print("开始生成测试图像...")
# 1. 创建一张 40x40 的黑白十字架测试图
img_clean = -np.ones((40, 40))
img_clean[10:30, 15:25] = 1
img_clean[15:25, 10:30] = 1
# 2. 添加噪点 (25% 的像素被翻转)
img_noisy = add_noise(img_clean, noise_ratio=0.25)
# 3. 使用 MRF 进行去噪
print("开始进行 MRF 模拟退火去噪...")
img_denoised = mrf_denoising(img_noisy, iter_max=15, T_init=3.0, T_end=0.1)
# 4. 画图对比
print("去噪完成,正在生成对比图...")
fig, axes = plt.subplots(1, 3, figsize=(12, 4))
axes[0].imshow(img_clean, cmap='gray')
axes[0].set_title("Original (Ground Truth)")
axes[1].imshow(img_noisy, cmap='gray')
axes[1].set_title("Noisy Observation (Input)")
axes[2].imshow(img_denoised, cmap='gray')
axes[2].set_title("MRF Denoised Output")
for ax in axes:
ax.axis('off')
plt.tight_layout()
plt.show()
开始生成测试图像...
开始进行 MRF 模拟退火去噪...
Iteration 1/15, Temp = 3.00
Iteration 2/15, Temp = 2.35
Iteration 3/15, Temp = 1.85
Iteration 4/15, Temp = 1.45
Iteration 5/15, Temp = 1.14
Iteration 6/15, Temp = 0.89
Iteration 7/15, Temp = 0.70
Iteration 8/15, Temp = 0.55
Iteration 9/15, Temp = 0.43
Iteration 10/15, Temp = 0.34
Iteration 11/15, Temp = 0.26
Iteration 12/15, Temp = 0.21
Iteration 13/15, Temp = 0.16
Iteration 14/15, Temp = 0.13
Iteration 15/15, Temp = 0.10
去噪完成,正在生成对比图...

你会看到三张图。输入给计算机的是一张如同雪花屏一样、满是噪点的图片(中间图)。 但在 MRF 势能规则(鼓励相邻像素同色) 的引导下,在 模拟退火 的大局控制下,经过 15 次全图的 Gibbs 采样扫描,图像的噪点像被施了魔法一样奇迹般地消失了,几乎完美还原了最初的十字架图案(右图)!
结语
至此,这篇“马尔可夫随机场入门指南”就全部结束了。
从打破时间维度束缚的网格 (Lattice),到定义局部联系的团 (Clique);从主宰一切的吉布斯分布 (Gibbs Distribution),到抽丝剥茧的 Gibbs 采样与模拟退火。
希望你能通过这套数学与代码交织的旅程,真切地感受到概率图模型那令人窒息的数学之美!
Scan to Share
微信扫一扫分享