为什么我们需要 MCMC?
一言蔽之,因为很多分布只知道未归一化形式,传统抽样/积分方法失效。
目标:从复杂分布 $\pi(x)$(常常只是“未归一化”的 $\tilde\pi(x)\propto \pi(x)$)中抽样,或计算期望/边际:
$$ \mathbb{E}_\pi[f(X)] \;=\; \int f(x)\,\pi(x)\,dx. $$现实里难点:
- 高维性:维度一高,网格/数值积分指数爆炸;
- 归一化常数未知:贝叶斯里后验 $\pi(\theta\mid y)\propto p(y\mid \theta)p(\theta)$ 的分母 $p(y)=\int p(y\mid \theta)p(\theta)\,d\theta$ 常算不出;
- 多峰/强相关:拒绝采样、重要性采样的方差会非常大或“权重退化”。
Monte Carlo 的核心思路:有了样本 $x^{(1)},\dots,x^{(T)}\sim \pi$,就能用样本均值
$$ \frac{1}{T}\sum_{t=1}^T f\!\big(x^{(t)}\big) $$近似 $\mathbb{E}_\pi[f(X)]$。问题是如何从 $\pi$ 抽样?这正是 MCMC 要解决的:不要求知道归一化常数、只需能计算 $\tilde\pi(x)$(或其对数),就能构造一个“会长期停在 $\pi$”的随机过程来取样。
MCMC 与其它路线的对比(直觉层面):
- 变分推断(VI):快、可扩展,但用“可解的近似族”逼近,存在近似偏差;
- SMC/粒子法:适合序贯问题,但设计与退火/重采样较复杂;
- MCMC:渐近无偏(跑得够久可以任意逼近 $\pi$),但样本相关、计算可能昂贵,需要诊断与调参。
示例
假设我们想从下面的分布采样:
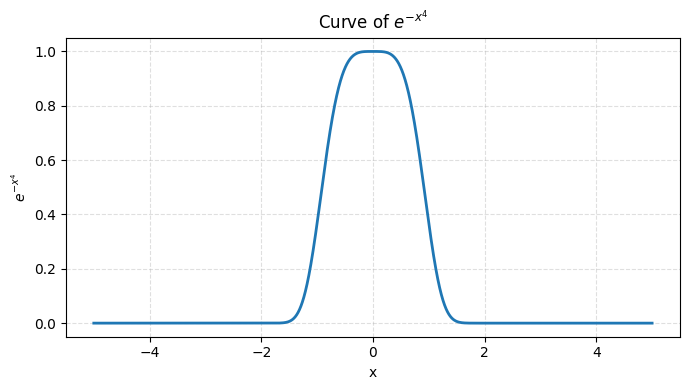
$$ \pi(x) \propto e^{-x^4}, \quad x \in \mathbb{R}. $$- 这是个“超级尖”的单峰分布。
- 没有归一化常数 $Z=\int e^{-x^4}\,dx$,手工算不出来。
- 想计算期望 $\mathbb{E}[X^2]$。
👉 问题:
- 直接积分没法做(解析不可解)。
- 拒绝采样需要一个“合适的包络函数”,但这里分布尾部特别重,难找。
👉 直观结论: 这就是 MCMC 登场的场景:我们只要能计算 $\tilde\pi(x)=e^{-x^4}$,即未归一化密度,就能设计一个马尔可夫链来收敛到它。
# 画出e^{-x^4} 分布的图像
import numpy as np
import matplotlib.pyplot as plt
# 自变量范围(-5 到 5 基本能看到主要形状)
x = np.linspace(-5, 5, 4001)
y = np.exp(-x**4)
plt.figure(figsize=(7, 4))
plt.plot(x, y, lw=2)
plt.title(r"Curve of $e^{-x^4}$")
plt.xlabel("x")
plt.ylabel(r"$e^{-x^4}$")
plt.grid(True, ls="--", alpha=0.4)
plt.tight_layout()
plt.show()
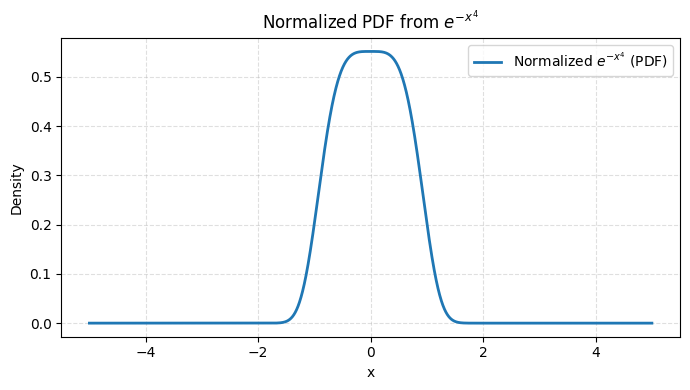
# 归一化 e^{-x^4} 使其成为概率密度函数 (PDF)
Z = np.trapezoid(y, x) # 数值积分
pdf = y / Z
plt.figure(figsize=(7, 4))
plt.plot(x, pdf, lw=2, label="Normalized $e^{-x^4}$ (PDF)")
plt.title(r"Normalized PDF from $e^{-x^4}$")
plt.xlabel("x")
plt.ylabel("Density")
plt.grid(True, ls="--", alpha=0.4)
plt.legend()
plt.tight_layout()
plt.show()
从马尔可夫链到抽样
一言蔽之,通过构造“正确的马尔可夫链”,让它的平稳分布就是目标分布;轨迹的长期分布 ≈ 目标分布。
把抽样问题变成“造一条链”
设状态空间 $\mathsf{X}$,想要样本来自目标分布 $\pi$。我们不直接抽样,而是构造转移核 $P(x,A)=\Pr(X_{t+1}\in A\mid X_t=x)$,使得 $\pi$ 是它的平稳分布(stationary/invariant):
$$ \pi(A) \;=\; \int_{\mathsf{X}} \pi(dx)\,P(x,A),\quad \forall A. $$直觉:如果你在 $\pi$ 下随机抽一个起点,然后按 $P$ 走一步,分布不变。如此“分布不变”的随机游走,一直走、一直停留在 $\pi$ 上。
保证“能到达、无周期、会遗忘起点”
仅有“平稳”不够;我们还需要这条链收敛到 $\pi$。常见充分条件:
- 不可约(irreducible):从任何地方都有正概率在有限步内到达任何“有质量”的区域;
- 非周期(aperiodic):不被固定的周期卡住;
- 合理的“返归/复现性”(Harris recurrence 等技术条件)。
有了这些,经典结果告诉我们:无论初始分布如何,随着时间 $t\to\infty$,分布 $P^t(x_0,\cdot)$ 在 total variation 距离下收敛到 $\pi$:
$$ \big\|P^t(x_0,\cdot)-\pi\big\|_{\mathrm{TV}}\to 0. $$于是,丢掉前期样本(burn-in),后续轨迹近似来自 $\pi$。
为什么“未归一化也行”
很多 MCMC 构造只需要比例 $\tilde\pi(x)\propto \pi(x)$。原因在于详细平衡/可逆性(见下一节):只用比值 $\tilde\pi(y)/\tilde\pi(x)$ 就能保证“对称流量”相等,从而得到 $\pi$ 为平稳分布。无需 $Z$ 是 MCMC 的关键优势。
示例
为了避免引入具体算法,我们先用最熟悉的分布:均匀分布来说明。
设目标分布是
$$ \pi(x) = \text{Uniform}\{1,2,3\}. $$我们设计一个马尔可夫链:
- 从 1、2、3 这三个状态中游走;
- 在每个位置,都等概率跳到另一个位置;
- 例如在 1 时,以 0.5 概率跳到 2,以 0.5 概率跳到 3。
👉 这个转移矩阵 P:
$$ P=\begin{bmatrix} 0 & 0.5 & 0.5 \\ 0.5 & 0 & 0.5 \\ 0.5 & 0.5 & 0 \end{bmatrix}. $$我们来跑一下,看它分布如何演化。
import numpy as np
import matplotlib.pyplot as plt
# 转移矩阵 P
P = np.array([
[0.0, 0.5, 0.5],
[0.5, 0.0, 0.5],
[0.5, 0.5, 0.0]
])
# 初始分布:全在 state 1
dist = np.array([1.0, 0.0, 0.0])
history = [dist]
# 演化 20 步
for t in range(20):
dist = dist @ P
history.append(dist)
history = np.array(history)
# 理论平稳分布(均匀)
pi = np.array([1/3, 1/3, 1/3])
# 绘图
plt.figure(figsize=(6,4))
for i in range(3):
plt.plot(history[:,i], label=f"State {i+1}")
plt.axhline(pi[0], color="k", linestyle="--", label="Stationary dist.")
plt.xlabel("Step")
plt.ylabel("Probability")
plt.title("Markov chain approaching uniform distribution")
plt.legend()
plt.show()
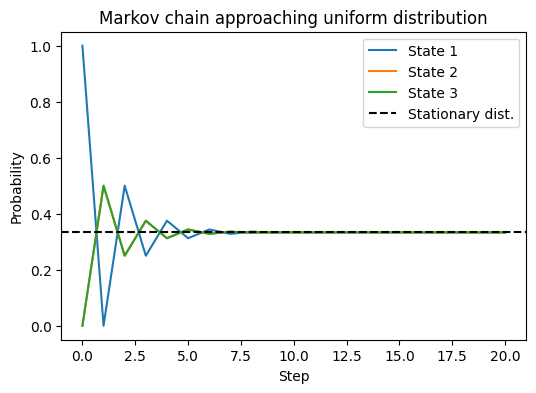
可以看到:
- 一开始分布全在 state 1;
- 随着转移步数增加,三条曲线逐渐趋近于 $1/3$;
- 最终收敛到平稳分布(均匀分布)。
👉 直觉: 马尔可夫链的“走动”让我们即使不直接从 $\pi$ 抽样,也能靠“长期停留比例”实现从 $\pi$ 取样。
理论与直觉
为什么可行、为何会收敛
一言蔽之,
- 平稳分布存在,且满足详细平衡 → 正确性。
- 收敛速度(混合时间)影响样本质量。
- 自相关越小,ESS 越大,链越“高效”。
详细平衡(reversibility)与平稳
若存在 $\pi$ 使得
$$ \pi(dx)\,P(x,dy) \;=\; \pi(dy)\,P(y,dx) \quad (\text{对称流量}) $$则称链对 $\pi$ 可逆,并可推出 $\pi$ 为平稳分布。
直觉:从 $\pi$ 出发,正向一步与“反向一步”的联合分布相同,整体“无净流”,所以稳态“不会被扰动”。
许多 MCMC 算法(MH、Gibbs、HMC 等)都在显式或隐式地构造这种可逆性/不变性。
收敛:遍历定理、LLN、CLT
当链是遍历的(不可约、非周期且适当返归),有:
遍历定理 / 马尔可夫链大数定律
$$ \frac{1}{T}\sum_{t=1}^T f(X_t) \;\xrightarrow{a.s.}\; \mathbb{E}_\pi[f(X)]. $$这保证了用轨迹均值估计期望是一致的。
中心极限定理(CLT)(在几何遍历等条件下)
$$ \sqrt{T}\Big(\bar f_T-\mathbb{E}_\pi[f]\Big)\ \Rightarrow\ \mathcal N\!\Big(0,\ \sigma_f^2\Big), $$其中
$$ \sigma_f^2 \;=\; \mathrm{Var}_\pi(f)\Big(1+2\sum_{k=1}^\infty \rho_k\Big), $$$\rho_k$ 是滞后 $k$ 的自相关。定义积分自相关时间(IACT)
$$ \tau_{\text{int}} \;=\; 1+2\sum_{k\ge1}\rho_k, $$则有效样本量 $\mathrm{ESS}\approx T/\tau_{\text{int}}$。 直觉:相关越强($\rho_k$ 衰减慢),每个样本信息量越低,ESS 越小。
混合时间、谱间隙与几何收敛
混合时间(mixing time)刻画 $P^t$ 到 $\pi$ 的接近速度,常用 TV 距离定义:
$$ \tau(\varepsilon)\;=\;\min\{t:\ \sup_{x_0}\|P^t(x_0,\cdot)-\pi\|_{\mathrm{TV}}\le \varepsilon\}. $$对有限可逆链,收敛速度与谱间隙 $\gamma=1-\lambda_\star$(除 1 外最大特征值 $\lambda_\star$)密切相关:$\tau(\varepsilon)$ 典型地与 $\frac{1}{\gamma}\log(1/\varepsilon)$ 同阶。 直觉:$\gamma$ 大 ⇒ “回忆性弱、遗忘快”,混合更快。
导通/瓶颈(conductance)刻画“跨区穿越难度”,与 $\gamma$ 通过 Cheeger 不等式相关。 直觉:分布多峰、峰间“峡谷”很深 ⇒ 导通小 ⇒ 混合慢(易“困在一个峰”)。
Burn-in、Thinning、诊断(从理论到实践)
Burn-in:前期“还没靠近 $\pi$”的样本会带偏估计,丢弃一段通常更稳妥。
Thinning:为减存储/相关常“隔点取样”,但从方差最小化角度不一定必要;很多情况下保留全部样本再用 IACT/ESS 做正确方差估计更好。
诊断(直觉导向):
- Trace 是否“游走自如”且无明显漂移;
- ACF/ESS:相关衰减是否够快;
- 多链 R-hat:多初值链是否混到一起;
- 多峰问题:是否出现“卡峰”(长滞留 + 突然跳峰)的模式。
为什么 MCMC 会“既能走、又能停在高密度区”
把 $\pi$ 看成玻尔兹曼分布:$\pi(x)\propto e^{-U(x)}$,$U(x)=-\log \tilde\pi(x)$ 类似“能量地形”。MCMC 像在地形里随机热运动:
- 在**低能量(高密度)**区域更愿意停留;
- 但通过“扰动/动量/接受-拒绝”等机制,仍有机会跨越能垒去探索其它区域;
- 只要机制保证不变分布是 $\pi$,且链遍历,长期统计就会正确。
示例
我们造一个“慢混合”的链:
- 状态 $\{0,1\}$,
- 从 0 出发,以 0.95 概率留在原地,0.05 概率跳到 1;
- 从 1 出发同理。
👉 虽然它的平稳分布仍是均匀 $[0.5,0.5]$,但“相关性”很强。
import numpy as np
import matplotlib.pyplot as plt
# 构造二状态链(黏滞性强)
P_slow = np.array([
[0.95, 0.05],
[0.05, 0.95]
])
# 模拟轨迹
T = 5000
x = np.zeros(T, dtype=int)
for t in range(1, T):
x[t] = np.random.choice([0,1], p=P_slow[x[t-1]])
# 计算自相关函数
def autocorr(x, lag):
n = len(x)
x_mean = np.mean(x)
num = np.sum((x[:n-lag]-x_mean)*(x[lag:]-x_mean)) # 自协方差
den = np.sum((x-x_mean)**2) # 方差
return num/den
lags = np.arange(50)
acfs = [autocorr(x, lag) for lag in lags]
# 绘图
plt.figure(figsize=(6,4))
plt.bar(lags, acfs)
plt.xlabel("Lag")
plt.ylabel("Autocorrelation")
plt.title("ACF of slow-mixing 2-state chain")
plt.show()
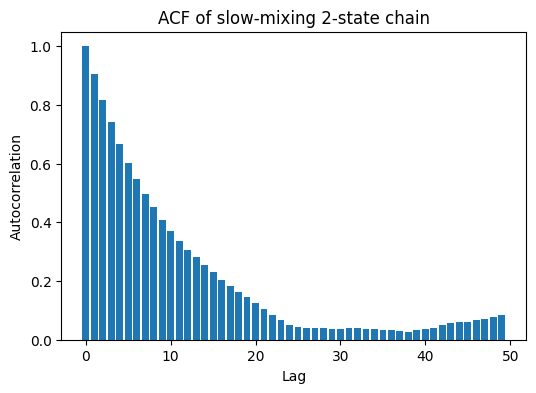
这里你能看到:
- 自相关函数 (ACF) 衰减非常慢;
- 意味着相邻样本高度依赖,有效样本数 (ESS) 远小于总步数。
👉 直觉总结:
- 马尔可夫链一定能收敛到平稳分布(如果条件满足);
- 但“混合速度”不同:有的链走几步就均衡,有的链拖很久;
- 在 MCMC 中,慢混合链的效率差,得到的样本“信息量少”。
实践层面的关键信号灯(不涉及具体算法)
只需 $\tilde\pi(x)$:能算对数密度 up to constant,就能上 MCMC。
三件事必须兼顾:
- 不变性($\pi$ 是平稳)——不变则长期正确;
- 可到达(不可约/非周期)——到不了就谈不上;
- 混合快(谱间隙/导通/IACT 小)——否则 ESS 太低、代价太大。
误差评估:用 IACT/ESS + 马尔可夫链 CLT 给 MC 方差和置信区间。
多峰警告:多峰 + 高维相关常导致亚稳态(metastability),这时要用更“会爬山过谷”的算法或策略(退火、平行温度、梯度方法等)提升导通。
小结
目的:从复杂 $\pi$ 估计期望/抽样;不需要归一化常数。
方法:造一个链 $P$ 使 $\pi$ 不变(常用详细平衡)。
条件:不可约 + 非周期 + 适当返归 ⇒ $P^t\to\pi$。
评估:
- 收敛(burn-in 后) + 混合(IACT/ESS、谱间隙、导通)
- 诊断:Trace、ACF、R-hat、多链一致性
误差:$\mathrm{ESS}\approx T/\tau_{\text{int}}$,CLT 给置信区间。
难点:多峰/高维相关 ⇒ 混合慢;需要更好的“移动策略”。