Gibbs Sampler is an algorithm to build a Markov Chain having a given N-dimension limit distribution, exploring its conditional distribution.
分而治之的智慧 (The “Divide and Conquer” Intuition)
痛点回顾: 在高维空间(比如 100 维)做 MH 采样,想一次性提议一个新的 100 维向量 $x_{new}$ 且被接受,是非常难的。这就像试图一次性猜中 100 个硬币的正反面。
- 虽然我们可以把多维问题通过组合降维为一个一维问题。但是当维度变大并且每个维度的状态空间也很大的时候,降维为一个一维问题后的状态空间会极大以至于解决极为困难。
Gibbs 的策略: 降维打击。
- 我们不一次变动所有维度。
- 每次只更新一个维度,把其他 99 个维度视为常量(固定住)。
直观类比:
- MH 算法:像直升机一样在地图上随机跳。
- Gibbs 采样:像在曼哈顿街头走路,每次只能沿东西方向走,或者沿南北方向走(Axis-aligned moves)。
MH 算法的困境:高维度的“彩票”
想象一下,你正在做一个 100 维 的采样任务(比如生成一张 10x10 像素的小图片,每个像素是一个维度)。
在 Metropolis-Hastings (MH) 中,为了生成下一个样本,你通常需要设计一个提议分布 $Q$。如果你尝试一次性更新所有 100 个像素(维度):
- 你是在问:“嘿,这 100 个数字组成的新组合,看起来像一张合理的图吗?”
- 在一个 100 维的空间里,随机瞎猜一个“好点”的概率就像中彩票一样低!
- 结果: 你的提议几乎总是被拒绝。接受率接近 0,电脑空转一天也没动静。
Gibbs 的策略:一次只做一件事
Gibbs Sampling 说:“别贪心。既然同时猜 100 个数字太难,那我们一次只猜 1 个数字怎么样?”
它的逻辑是这样的:
- 锁定第 2 到第 100 个维度(假装它们是常数)。
- 现在,问题变成了:“在其他人都固定的情况下,第 1 个维度的最佳值应该是多少?”
- 这是一个 1 维 的问题!这太容易了。我们直接从这个**条件分布 (Conditional Distribution) **里抽一个数出来。
- 更新第 1 个维度。接下来,锁定第 1、3…100 个维度,只更新第 2 个…
核心哲学: 将一个复杂的 $N$ 维问题,拆解成 $N$ 个简单的 $1$ 维问题。
数学维度:将联合分布(joint distribution)转换为条件分布(conditional distribution)
视觉直觉:曼哈顿漫步 (Manhattan Walk)
为了形象地理解它的轨迹,我们对比一下 MH 和 Gibbs 在二维地图上的走法。
假设我们要爬一座山(目标分布 $\pi$),山顶在右上角。
🚁 MH 算法:直升机式跳跃
- 动作: 它不管地形,随机向任意方向(斜着跳、远跳)扔出一个探测器。
- 轨迹: 可以在地图上任意角度移动。
- 代价: 如果跳到了悬崖(低概率区),就会被弹回来(拒绝)。
🚶 Gibbs 采样:曼哈顿街头漫步
- 动作: 想象你在曼哈顿这种棋盘式街道的城市里走路。你不能穿墙,不能斜着走。你只能沿着街道(坐标轴)走。
- 轨迹:
- 先沿着 X 轴 移动(更新 $x$,保持 $y$ 不变)。
- 再沿着 Y 轴 移动(更新 $y$,保持 $x$ 不变)。
- 重复。
- 特征: 它的轨迹永远是直角折线 (Zig-zag),像是在爬楼梯。
为什么这么做容易?(切片思维)
你可能会问:“只是换个方向走,为什么就不用拒绝了?”
想象一个二维的正态分布(像一个小山包)。Gibbs 采样的每一步,实际上是在对这个山包做 “切片” (Slicing)。
- 当你固定 $y=5$ 时,你就像是用一把刀,在 $y=5$ 的位置水平切开了这个山包。
- 切面是一个 1 维的曲线。
- Gibbs 说:“请直接在这个 1 维曲线上采样。”
- 既然你是直接从这个切面上拿数据,拿到的肯定是合理的,所以接受率 = 100%!
数学原理
提供联合分布等价于提供所有的“满条件分布”
通常我们认为:联合分布 (Joint Distribution) $P(x_1, \dots, x_n)$ 包含了所有的信息,有了它,求边缘分布或条件分布都是简单的积分或除法运算。但反过来就没那么直观了:如果我只给你所有的“满条件分布” (Full Conditionals) $P(x_i | x_{-i})$,你真的能唯一还原出原来的联合分布吗?
答案是:是的,但有一个前提条件(正性假设)。 这个结论被称为 Brook’s Lemma (布鲁克引理)。
证明
第一步:Joint $\Rightarrow$ Conditionals (简单方向)
这个方向非常直观,其实就是条件概率的定义。假设我们要从联合分布 $P(x_1, \dots, x_n)$ 推导第 $i$ 个变量的满条件分布。
$$ P(x_i | x_{-i}) = \frac{P(x_1, \dots, x_n)}{P(x_{-i})} = \frac{P(x_1, \dots, x_n)}{\int P(x_1, \dots, x_n) dx_i} $$显然,只要给定了联合分布,分母(边缘分布)可以通过积分算出,分子是已知的,所以所有的满条件分布也就唯一确定了。这不需要任何技巧。
第二步:Conditionals $\Rightarrow$ Joint (困难方向:Brook’s Lemma)
这是 Gibbs Sampling 的核心。如果没有这个引理,我们拿着一堆条件分布去采样,最后根本不知道自己收敛到了什么联合分布上。
我们需要证明:仅通过所有的满条件分布,可以重构出联合分布(差一个归一化常数)。
为了让证明不那么枯燥,我们以 二维 (Bivariate) 情况为例。假设有两个变量 $x$ 和 $y$。
- 设定目标。我们要找到 $\frac{P(x, y)}{P(x_0, y_0)}$ 的表达式,其中 $(x_0, y_0)$ 是任意选定的一个参考点(基准点)。如果我们能用条件分布把这个比值写出来,那就证明了联合分布是可以被还原的。
- 利用恒等式。我们把目标比值拆解成两步走(从基准点 $(x_0, y_0)$ 走到 $(x, y)$):$$\frac{P(x, y)}{P(x_0, y_0)} = \frac{P(x, y)}{P(x_0, y)} \cdot \frac{P(x_0, y)}{P(x_0, y_0)}$$注意看,我们插入了一个中间状态 $(x_0, y)$。
- 展开第一项。利用贝叶斯定义:$P(x, y) = P(x | y) P(y)$ 和 $P(x_0, y) = P(x_0 | y) P(y)$。代入第一项:$$\frac{P(x, y)}{P(x_0, y)} = \frac{P(x | y) \cancel{P(y)}}{P(x_0 | y) \cancel{P(y)}} = \frac{P(x | y)}{P(x_0 | y)}$$看! 边缘分布 $P(y)$ 消掉了!这一项完全只由条件分布决定。
- 展开第二项。同样利用定义:$P(x_0, y) = P(y | x_0) P(x_0)$ 和 $P(x_0, y_0) = P(y_0 | x_0) P(x_0)$。代入第二项:$$\frac{P(x_0, y)}{P(x_0, y_0)} = \frac{P(y | x_0) \cancel{P(x_0)}}{P(y_0 | x_0) \cancel{P(x_0)}} = \frac{P(y | x_0)}{P(y_0 | x_0)}$$看! 边缘分布 $P(x_0)$ 也消掉了!这一项也只由条件分布决定。
- 合并结果 (Brook’s Lemma for 2D)将两步合并,我们得到:$$P(x, y) \propto \frac{P(x | y)}{P(x_0 | y)} \cdot \frac{P(y | x_0)}{P(y_0 | x_0)}$$
结论:看,等式右边全部都是条件分布。这意味着,只要你告诉我 $P(x|y)$ 和 $P(y|x)$ 长什么样,我就能通过这个公式,算出任意一点 $(x, y)$ 相对于基准点 $(x_0, y_0)$ 的概率比值。这就唯一确定了联合分布 $P(x, y)$ 的形状(up to a constant)。
推广到 N 维 (Brook’s Lemma 通式)
这个逻辑可以推广到 $n$ 维。我们要计算 $\frac{P(x_1, \dots, x_n)}{P(x_1^0, \dots, x_n^0)}$。
我们可以像走楼梯一样,每次只改变一个坐标,从 $\mathbf{x}^0$ 走到 $\mathbf{x}$:$(0,0,0) \to (x_1, 0, 0) \to (x_1, x_2, 0) \to (x_1, x_2, x_3)$。
公式长这样:
$$P(\mathbf{x}) \propto \prod_{i=1}^n \frac{P(x_i | x_1, \dots, x_{i-1}, x_{i+1}^0, \dots, x_n^0)}{P(x_i^0 | x_1, \dots, x_{i-1}, x_{i+1}^0, \dots, x_n^0)}$$重要的前提:正性假设 (Positivity Condition)
在上面的证明中,你有没有发现一个潜在的 Bug?我们在做除法!分母出现了 $P(x_0 | y)$ 之类的项。
如果在状态空间中,概率 $P(x)$ 在某些地方是 0 怎么办?除以 0 是非法的。
这就是 Hammersley-Clifford 定理 的要求:联合分布必须满足正性假设 (Positivity Assumption)。 即:对于任意 $x_i$,如果边际上可能发生,那么它们的组合 $(x_1, \dots, x_n)$ 的概率必须 大于 0。
反例(条件不能决定联合的情况):想象一个棋盘,只有白色的格子有概率(概率为 1),黑色的格子概率为 0。
- $P(x|y)$ 只能告诉你:如果在第 $y$ 行,一定要在白格子里。
- 但是,它无法告诉你,这一行的白格子 和 那一行的白格子 谁的概率更高。因为它们之间可能被黑格子(概率为0的深渊)隔开了,你没法通过“中间路径”走过去做比较(比值链条断了)。
为什么不用拒绝?(Why Acceptance is 100%?)
Gibbs Sampling 本质上就是接受率 $\alpha=1$ 的 Metropolis-Hastings 算法。
直观理解:为什么不需要“审核”?
先不用公式,咱们用个生活中的例子。
- Metropolis (盲猜):你要去买衣服。你闭着眼睛随手抓一件(提议 $Q$),然后睁开眼看看合不合身(计算 $\pi$)。如果不合身,你就把它扔回去(拒绝)。因为你是瞎抓的,所以必须有“试穿和拒绝”的机制来保证质量。
- Gibbs (定制):你走进一家裁缝店。裁缝量了你的尺寸(固定住其他变量 $x_{-i}$),然后直接按照这个尺寸给你做了一件衣服(从条件分布 $P(x_i | x_{-i})$ 中采样)。请问:这件量身定做的衣服,还需要“审核”吗?不需要。因为它本身就是根据正确的规则生成的,所以它天生就是合法的。
数学证明:MH 接受率公式的完美对消
现在我们用数学语言来把这个“量身定做”的过程翻译一遍。
假设我们有两个变量 $x$ 和 $y$。当前状态:$(x, y)$
- 动作: 我们决定更新 $x$,把 $y$ 固定住。
- Gibbs 的提议: 直接从满条件分布中采样一个新的 $x^*$。
这意味着,我们的 提议分布 (Proposal Distribution) $Q$ 就是条件概率:
$$Q(\text{new} | \text{old}) = Q(x^*, y | x, y) = P(x^* | y)$$注意:提议只取决于 $y$,跟旧的 $x$ 没关系
同理,反向提议(从新变回旧)的概率是:
$$Q(\text{old} | \text{new}) = Q(x, y | x^*, y) = P(x | y)$$现在,我们要把这些代入 MH 接受率公式:
$$\alpha = \frac{\pi(\text{new})}{\pi(\text{old})} \times \frac{Q(\text{old} | \text{new})}{Q(\text{new} | \text{old})}$$- 代入目标分布 $\pi$。目标分布就是联合分布 $P(x, y)$。$$\text{Target Ratio} = \frac{P(x^*, y)}{P(x, y)}$$
- 代入提议分布 $Q$。就是刚才写的条件分布。$$\text{Proposal Ratio} = \frac{P(x | y)}{P(x^* | y)}$$
- 合并并利用乘法公式$$A = \frac{P(x^*, y)}{P(x, y)} \times \frac{P(x | y)}{P(x^* | y)}$$利用概率乘法公式:联合概率 = 条件概率 $\times$ 边缘概率
- 分子展开:$P(x^*, y) = P(x^* | y) \cdot P(y)$
- 分母展开:$P(x, y) = P(x | y) \cdot P(y)$
- 代回去:$$A = \frac{\mathbf{P(x^* | y)} \cdot \mathbf{P(y)}}{\mathbf{P(x | y)} \cdot \mathbf{P(y)}} \times \frac{\mathbf{P(x | y)}}{\mathbf{P(x^* | y)}}$$
- 见证奇迹 (The Cancellation)拿出你的红笔,开始消消乐:
- $P(y)$:分子分母都有(因为 $y$ 没变),消掉!
- $P(x^ | y)$*:前面的分子有,后面的分母有,消掉!
- $P(x | y)$:前面的分母有,后面的分子有,消掉!
- 最终结果:$$A = 1$$
所以接受率 $\alpha = \min(1, A) = 1$。
Gibbs Sampling 的正确性(缺)
##
算法流程
假设我们要从一个 $n$ 维的联合分布 $P(x_1, x_2, \dots, x_n)$ 中进行采样。
- 初始化 (Initialization)。选择一个初始状态 $\mathbf{x}^{(0)} = (x_1^{(0)}, x_2^{(0)}, \dots, x_n^{(0)})$。这个点可以是在状态空间内随机选取的,或者根据先验知识选定的。
- 迭代循环 (The Iteration Loop)对于每一次迭代 $t = 1, 2, \dots, T$:我们要依次更新向量 $\mathbf{x}$ 中的每一个分量。请注意,更新后的分量会立即参与到下一个分量的采样中。
- 更新第 1 维:从第一个满条件分布中采样新值 $x_1^{(t)}$:$$x_1^{(t)} \sim P(x_1 \mid x_2^{(t-1)}, x_3^{(t-1)}, \dots, x_n^{(t-1)})$$
- 更新第 2 维:利用刚采到的 $x_1^{(t)}$ 和旧的其余维度:$$x_2^{(t)} \sim P(x_2 \mid x_1^{(t)}, x_3^{(t-1)}, \dots, x_n^{(t-1)})$$
- 更新第 $i$ 维:$$x_i^{(t)} \sim P(x_i \mid x_1^{(t)}, \dots, x_{i-1}^{(t)}, x_{i+1}^{(t-1)}, \dots, x_n^{(t-1)})$$
- 更新第 $n$ 维:$$x_n^{(t)} \sim P(x_n \mid x_1^{(t)}, x_2^{(t)}, \dots, x_{n-1}^{(t)})$$
- 收集样本 (Data Collection)。将完成一轮更新后的向量 $\mathbf{x}^{(t)} = (x_1^{(t)}, x_2^{(t)}, \dots, x_n^{(t)})$ 记为一个样本。
更新顺序的不同策略
在实际操作中,更新顺序有几种不同的策略:
- 系统扫描 (Systematic Scan):
- 做法:严格按照 $1 \to 2 \to \dots \to n$ 的顺序循环。
- 特点:实现简单,最常用。
- 随机扫描 (Random Scan):
- 做法:每次随机抽取一个维度 $i \in \{1, \dots, n\}$ 进行更新。
- 特点:更容易满足理论上的细致平衡(Detailed Balance),在某些特定的数学证明中更受青睐。
- 分组/块采样 (Blocked Gibbs):
- 做法:如果 $x_1$ 和 $x_2$ 相关性极强,把它们打包在一起,从 $P(x_1, x_2 \mid \dots)$ 中同时采样。
- 特点:有效解决 Gibbs 在面对强相关变量时“走不动”(收敛慢)的问题。
代码实战
离散示例:二元离散系统 (Bivariate Discrete System)
假设有两个变量 $x$ 和 $y$,它们都是离散的,且只能取 $0$ 或 $1$。这就像是有两个开关,或者是两座只有两个区域的岛屿。
我们已知它们合在一起的概率表(这是我们的目标):
| x | y | P(x,y) | 描述 |
|---|---|---|---|
| 0 | 0 | 0.1 | 状态 (0,0) |
| 0 | 1 | 0.4 | 状态 (0,1) |
| 1 | 0 | 0.3 | 状态 (1,0) |
| 1 | 1 | 0.2 | 状态 (1,1) |
目标: 我们要在不知道这张表全貌的情况下,只通过局部规则采样,最终让样本的频率符合这个比例。
在离散 Gibbs 采样中,我们需要知道:如果固定一个,另一个该怎么变?
- 给定 $y$,求 $x$ 的条件分布 $P(x|y)$
- 如果 $y=0$:
- $P(x=0 | y=0) = \frac{P(0,0)}{P(0,0) + P(1,0)} = \frac{0.1}{0.1 + 0.3} = 0.25$
- $P(x=1 | y=0) = 0.75$
- 如果 $y=1$:
- $P(x=0 | y=1) = \frac{P(0,1)}{P(0,1) + P(1,1)} = \frac{0.4}{0.4 + 0.2} \approx 0.67$
- $P(x=1 | y=1) \approx 0.33$
- 如果 $y=0$:
- 给定 $x$,求 $y$ 的条件分布 $P(y|x)$
- 如果 $x=0$:
- $P(y=0 | x=0) = \frac{P(0,0)}{P(0,0) + P(0,1)} = \frac{0.1}{0.1 + 0.4} = 0.2$
- $P(y=1 | x=0) = 0.8$
- 如果 $x=1$:
- $P(y=0 | x=1) = \frac{0.3}{0.3 + 0.2} = 0.6$
- $P(y=1 | x=1) = 0.4$
- 如果 $x=0$:
import numpy as np
import matplotlib.pyplot as plt
# 1. 设定满条件分布 (依据上面的计算结果)
def sample_x_given_y(y):
if y == 0:
# P(x=0|y=0)=0.25, P(x=1|y=0)=0.75
return np.random.choice([0, 1], p=[0.25, 0.75])
else:
# P(x=0|y=1)=0.67, P(x=1|y=1)=0.33
return np.random.choice([0, 1], p=[0.67, 0.33])
def sample_y_given_x(x):
if x == 0:
# P(y=0|x=0)=0.2, P(y=1|x=0)=0.8
return np.random.choice([0, 1], p=[0.2, 0.8])
else:
# P(y=0|x=1)=0.6, P(y=1|x=1)=0.4
return np.random.choice([0, 1], p=[0.6, 0.4])
# 2. Gibbs 采样循环
def discrete_gibbs(n_iter):
samples = []
x, y = 0, 0 # 初始状态
for _ in range(n_iter):
x = sample_x_given_y(y) # 更新 x
y = sample_y_given_x(x) # 更新 y
samples.append((x, y))
return np.array(samples)
# 3. 运行并分析结果
n_iter = 10000
results = discrete_gibbs(n_iter)
# 计算每个状态出现的频率
unique, counts = np.unique(results, axis=0, return_counts=True)
frequencies = counts / n_iter
print("--- 离散 Gibbs 采样结果 ---")
for state, freq in zip(unique, frequencies):
print(f"状态 {state}: 采样频率 {freq:.4f}")
# 可视化前 50 步的路径
plt.figure(figsize=(6, 6))
plt.plot(results[:50, 0] + np.random.normal(0, 0.02, 50),
results[:50, 1] + np.random.normal(0, 0.02, 50),
'o-', alpha=0.5)
plt.xticks([0, 1])
plt.yticks([0, 1])
plt.title("Trace of First 50 Discrete Gibbs Steps\n(with small jitter for visibility)")
plt.xlabel("X state")
plt.ylabel("Y state")
plt.grid(True)
plt.show()
--- 离散 Gibbs 采样结果 ---
状态 [0 0]: 采样频率 0.1017
状态 [0 1]: 采样频率 0.4054
状态 [1 0]: 采样频率 0.2928
状态 [1 1]: 采样频率 0.2001
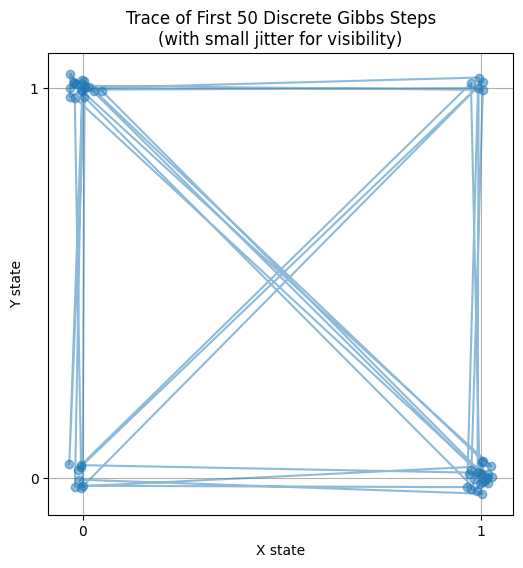
即便在如此简单的只有 4 个状态的离散空间里,Gibbs 依然表现得非常优雅:
- 收敛极快:对于简单的离散问题,Gibbs 几乎瞬间就能通过几次“全条件采样”锁定目标分布的比例。
- 路径特征:观察轨迹图(前 50 步),你会发现它在 $(0,0), (0,1), (1,0), (1,1)$ 这四个点之间跳跃。因为是直角移动,它总是先横着变,再竖着变。
- 应用场景:这种离散 Gibbs 采样是 图像去噪 (Image Denoising)(如 Ising 模型)和 隐含狄利克雷分布 (LDA) 等自然语言处理模型的核心技术。在那些场景下,我们有成千上万个离散变量(像素或单词), Gibbs 每次只翻转一个像素或更新一个单词的分类。
连续示例:二元正态分布 (Bivariate Normal Implementation)
我们要采样的目标是一个二维向量 $(x, y)$,服从标准二元正态分布:
- 均值:$\mu_x = 0, \mu_y = 0$
- 方差:$\sigma_x = 1, \sigma_y = 1$
- 相关系数:$\rho$ (rho)。这是一个 $[-1, 1]$ 之间的数,决定了 $x$ 和 $y$ 的关系有多紧密。
如果我们想直接从这里采样(比如用 Rejection Sampling),我们需要处理这个公式:
$$P(x, y) \propto \exp\left( -\frac{1}{2(1-\rho^2)} (x^2 - 2\rho xy + y^2) \right)$$这看起来就很麻烦,对吧?
现在我们使用 Gibbs Sampler。
根据多元高斯分布的性质,如果我们已知 $y$,那么 $x$ 的分布就是:
$$P(x | y) = \mathcal{N}(\text{均值}=\rho y, \text{方差}=1-\rho^2)$$反过来,如果我们已知 $x$,那么 $y$ 的分布就是:
$$P(y | x) = \mathcal{N}(\text{均值}=\rho x, \text{方差}=1-\rho^2)$$直观理解:
- 均值 $\rho y$:如果你知道 $y$ 是正的,且 $x, y$ 正相关 ($\rho>0$),那么 $x$ 大概率也是正的。所以 $x$ 的中心会向 $y$ 偏移。
- 方差 $1-\rho^2$:如果相关性很强 ($\rho \to 1$),方差趋近于 0。这意味着一旦 $y$ 确定了,$x$ 几乎也就确定了(没什么自由度)。
import numpy as np
import matplotlib.pyplot as plt
# --- 1. 参数设置 ---
rho = 0.8 # 相关系数 (Correlation)
n_samples = 2000 # 采样数量
start_x, start_y = -4.0, -4.0 # 故意从一个很远的角落开始
# --- 2. Gibbs Sampler ---
def run_gibbs_sampler(n, rho, start_x, start_y):
samples = np.zeros((n, 2))
x, y = start_x, start_y
# 标准差 (Scale) 是方差的平方根
# conditional variance = 1 - rho^2
cond_std = np.sqrt(1 - rho**2)
for i in range(n):
# A. 固定 y,采样 x
# x ~ N(rho * y, 1 - rho^2)
x = np.random.normal(loc=rho * y, scale=cond_std)
# B. 固定 x,采样 y (注意:这里用的是刚更新的 x)
# y ~ N(rho * x, 1 - rho^2)
y = np.random.normal(loc=rho * x, scale=cond_std)
samples[i] = [x, y]
return samples
# 运行采样
chain = run_gibbs_sampler(n_samples, rho, start_x, start_y)
# --- 3. 结果可视化 ---
plt.figure(figsize=(12, 5))
# 图 1: 轨迹细节 (前 50 步) - 看看它是怎么走的
plt.subplot(1, 2, 1)
plt.plot(chain[:50, 0], chain[:50, 1], 'o-', alpha=0.6, color='blue', markersize=4, label='Gibbs Path')
# 画出起点
plt.plot(start_x, start_y, 'ro', label='Start', markersize=8)
plt.title(f"Gibbs Trajectory (First 50 Steps)\nCorrelation rho={rho}")
plt.xlabel("X")
plt.ylabel("Y")
plt.legend()
plt.grid(True, alpha=0.3)
# 强制横纵比例一致,这样才能看出正态分布的椭圆形状
plt.axis('equal')
# 图 2: 最终分布散点图
plt.subplot(1, 2, 2)
plt.scatter(chain[:, 0], chain[:, 1], s=5, alpha=0.3, color='green')
plt.title(f"Final Samples (N={n_samples})\nTarget: Bivariate Normal")
plt.xlabel("X")
plt.ylabel("Y")
plt.axis('equal')
plt.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
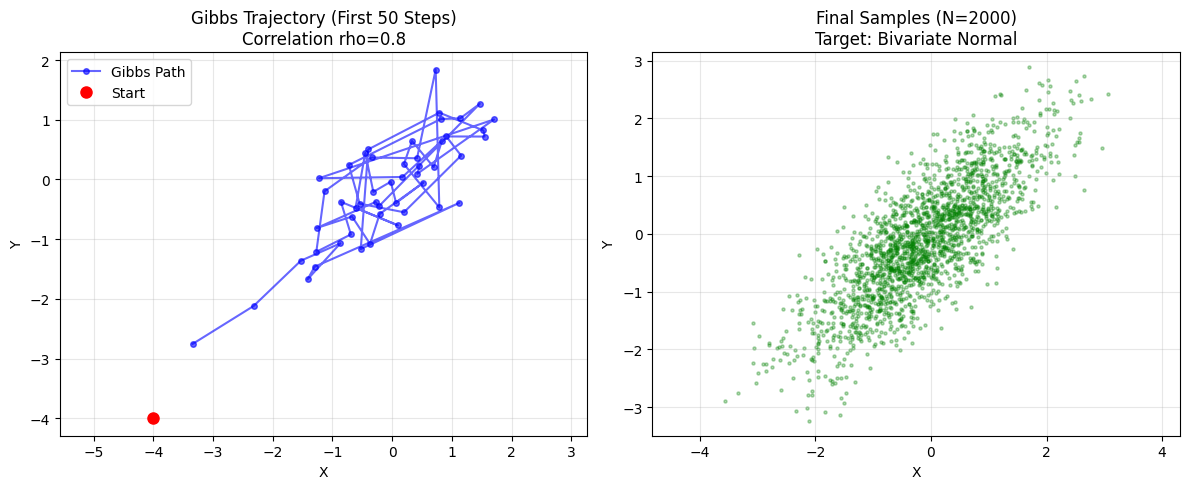
仔细观察上面的左图 (轨迹图)。
- 曼哈顿式移动 (Orthogonal Moves)
- 虽然我们在代码里只存了
[x, y]这个点,但实际上每次更新只变动一个坐标。 - 如果你把中间过程补全,它的真实路径其实是 “直角折线”:
- 先水平移动(更新 $x$)
- 再垂直移动(更新 $y$)
- 再水平移动…
- 这验证了 Gibbs Sampling “沿着坐标轴切片采样” 的本质。
- 虽然我们在代码里只存了
- Burn-in 的过程
- 小人从 $(-4, -4)$ 出发。
- 你会看到它在前几步迅速地向中心 $(0, 0)$ 靠拢。
- 这个过程非常快,可能只需要 5-10 步就进入了“椭圆”的主体区域。
Gibbs 的软肋——强相关性 (The Kryptonite: High Correlation)
- 主要缺陷: 虽然接受率是 100%,但这不代表它总是高效的。
- 场景模拟: 当两个变量高度相关($\rho = 0.99$)时,分布形状像一条细长的峡谷。
- 困境: Gibbs 只能横着走或竖着走。在狭窄的斜向峡谷里,它只能以极小的碎步像楼梯一样慢慢挪动(Slow Mixing)。
- 解决方案: Blocked Gibbs Sampling(打包更新)。
import numpy as np
import matplotlib.pyplot as plt
# --- 1. 参数设置 ---
rhos = {0: '无相关', 0.99: '极强相关'} # 相关系数 (Correlation)
n_samples = 2000 # 采样数量
start_x, start_y = -4.0, -4.0 # 故意从一个很远的角落开始
# --- 2. Gibbs Sampler ---
def run_gibbs_sampler(n, rho, start_x, start_y):
samples = np.zeros((n, 2))
x, y = start_x, start_y
# 标准差 (Scale) 是方差的平方根
# conditional variance = 1 - rho^2
cond_std = np.sqrt(1 - rho**2)
for i in range(n):
# A. 固定 y,采样 x
# x ~ N(rho * y, 1 - rho^2)
x = np.random.normal(loc=rho * y, scale=cond_std)
# B. 固定 x,采样 y (注意:这里用的是刚更新的 x)
# y ~ N(rho * x, 1 - rho^2)
y = np.random.normal(loc=rho * x, scale=cond_std)
samples[i] = [x, y]
return samples
# 运行采样
index = 1
for rho, rho_label in rhos.items():
chain = run_gibbs_sampler(n_samples, rho, start_x, start_y)
# --- 3. 结果可视化 ---
plt.figure(figsize=(12, 10))
# 图 1: 轨迹细节 (前 50 步) - 看看它是怎么走的
plt.subplot(2, 2, index)
plt.plot(chain[:50, 0], chain[:50, 1], 'o-', alpha=0.6, color='blue', markersize=4, label='Gibbs Path')
# 画出起点
plt.plot(start_x, start_y, 'ro', label='Start', markersize=8)
plt.title(f"Gibbs Trajectory (First 50 Steps)\nCorrelation rho={rho}")
plt.xlabel("X")
plt.ylabel("Y")
plt.legend()
plt.grid(True, alpha=0.3)
# 强制横纵比例一致,这样才能看出正态分布的椭圆形状
plt.axis('equal')
index += 1
# 图 2: 最终分布散点图
plt.subplot(2, 2, index)
plt.scatter(chain[:, 0], chain[:, 1], s=5, alpha=0.3, color='green')
plt.title(f"Final Samples (N={n_samples})\nTarget: Bivariate Normal")
plt.xlabel("X")
plt.ylabel("Y")
plt.axis('equal')
plt.grid(True, alpha=0.3)
index += 1
plt.tight_layout()
plt.show()
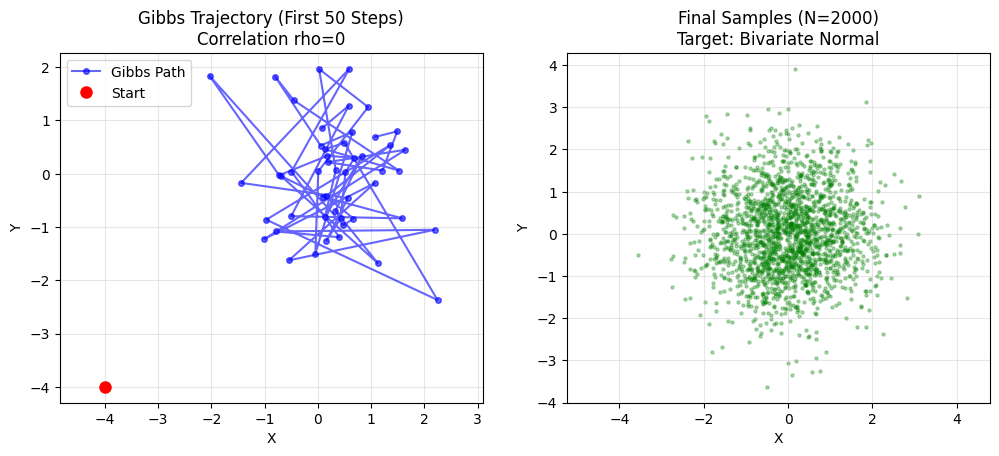
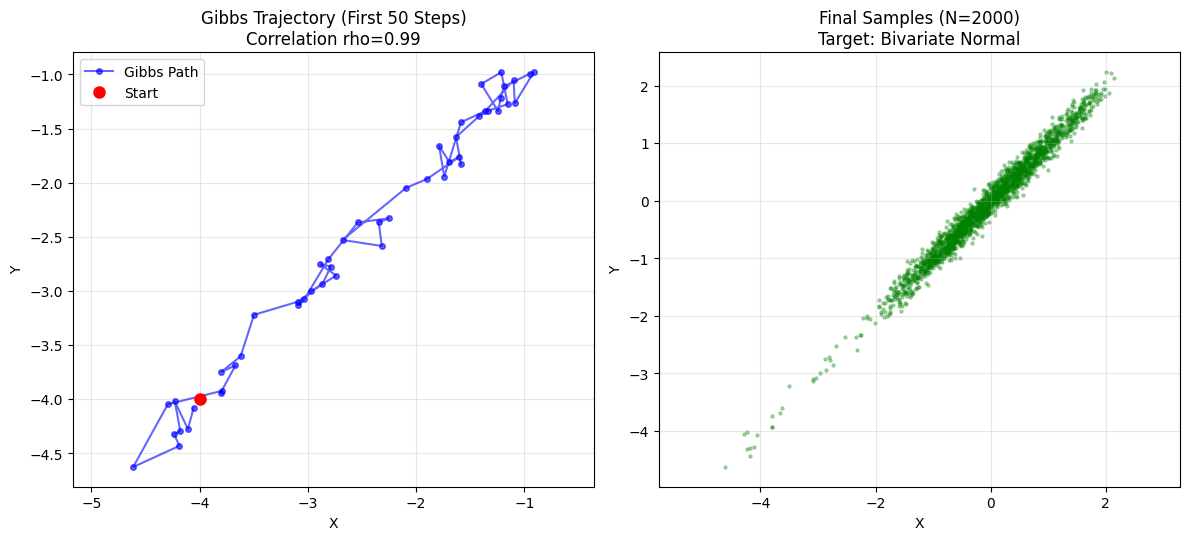
在上面的实验中,我们修改了相关值 rho。
- 设定 rho = 0 (无相关):
- 椭圆变成了一个 正圆。
- 小人可以在圆里随意跳跃,混合极快。
- 设定 rho = 0.99 (极强相关):
- 椭圆变成了一条 极细的线(峡谷)。
- 观察轨迹: 你会发现小人只能以此极小的碎步沿着对角线挪动。
- 原因: 当 $\rho=0.99$ 时,条件方差 $1-\rho^2$ 接近 0。这意味着 $P(x|y)$ 被锁死在 $y$ 附近极小的范围内。你虽然没有被拒绝(接受率100%),但你也走不远。
- 这就是 Gibbs Sampling 的软肋:在强相关分布中,收敛会变得非常慢。
Scan to Share
微信扫一扫分享