确定性优化(Deterministic optimization)
They are thought for convext function. If the function is not convext, we change to stochastic optimization.
| 算法 | 类别 | 利用信息 | 几何直觉 | 优点 | 缺点 | 对应 MCMC |
|---|---|---|---|---|---|---|
| 牛顿法 | 二阶 | 梯度 + 曲率 (Hessian) | 抛物面近似 (碗) | 收敛极快 | 计算 H 逆太贵 | 类似 Langevin (利用二阶) |
| 坐标下降法 | 零阶/一阶 | 单变量信息 | 沿坐标轴移动 | 简单,无需全梯度 | 强相关时收敛慢 | Gibbs Sampling |
| 最速下降法 | 一阶 | 梯度 | 切平面最陡方向 | 计算便宜,通用 | 容易震荡,收敛慢 | 类似 HMC / MCMC |
优化问题的定义 (Definition of Optimization Problem)
在数学层面,一个标准的优化问题通常被写成这种“八股文”格式:
$$\begin{aligned} & \underset{x}{\text{minimize}} & & f(x) \\ & \text{subject to} & & g_i(x) \le 0, \quad i = 1, \dots, m \\ & & & h_j(x) = 0, \quad j = 1, \dots, p \end{aligned}$$这里有三个主角:
- 决策变量 (Decision Variable, $x$):我们可以控制的旋钮(比如模型的参数权重)。
- 目标函数 (Objective Function, $f(x)$):我们的度量标准。通常是最小化“损失/成本”或最大化“收益/似然”。
- 注:最大化 $f(x)$ 等价于最小化 $-f(x)$,所以我们通常只研究最小化。
- 约束条件 (Constraints):
- 不等式约束 ($g_i \le 0$):比如“速度不能超过 100”。
- 等式约束 ($h_j = 0$):比如“能量必须守恒”。
目标函数 $f(x)$
为了能找到最低点,这个目标函数 $f(x)$ 必须遵守以下三条规则:
- 必须是“单值实数” (Scalar-Valued)
- 要求:不管输入 $x$ 是多少维的向量(比如你有100万个参数),$f(x)$ 输出的必须是一个单一的实数(Scalar)。
- 数学写法:$f: \mathbb{R}^n \to \mathbb{R}$
- 为什么?
- 因为优化问题的核心是 “比较”。我们需要能说出 $f(x_1) < f(x_2)$。如果 $f(x)$ 输出的是一个向量(比如“成本”和“时间”两个数),这就变成了“多目标优化”,那是另一个复杂的领域。在标准优化里,你必须把它们合成一个数(比如 $0.5 \times \text{成本} + 0.5 \times \text{时间}$)。
- 必须“有底” (Bounded Below)
- 这是为了保证 “最优解存在”。
- 要求:函数不能是无底洞。
- 反例:$f(x) = x$(定义域为全体实数)。
- 你想求最小化?我可以取 $-100, -10000, -\infty \dots$
- 你永远找不到最低点,因为根本没有最低点。算法会一直跑到内存溢出。
- 修正:通常我们要求存在一个实数 $M$,使得对于所有的 $x$,都有 $f(x) \ge M$。
- 为了“算法能跑”,通常还要更顺滑 (Smoothness):如果你想用牛顿法、梯度下降这些高级算法,函数 $f(x)$ 不能长得太随心所欲,它 需要满足连续性和可导性。
- 连续性 (Continuity) —— 路不能断
- 直觉:你在山上走,地形不能突然出现“悬崖断层”。
- 坏函数:阶梯函数(Step Function)。
- 比如 $x < 0$ 时 $f(x)=1$, $x \ge 0$ 时 $f(x)=0$。
- 这种函数很难优化,因为在断开的地方,你不知道该往哪迈步。
- 可导性 (Differentiability) —— 路不能有尖角
- 直觉:这是 “梯度下降” 的前提。
- 梯度(导数)代表坡度。如果函数有一个尖锐的折角,那一点是没有坡度的(导数不存在)。
- 坏函数:$f(x) = |x|$(绝对值函数)。
- 在 $x=0$ 这个尖尖的地方,导数没定义。
- 注:虽然它是凸函数,但标准的梯度下降在这里会失效(需要用次梯度 Sub-gradient)。
- 更坏的函数:$f(x)$ 处处不可导(比如股票走势图那样的锯齿)。这种只能用“零阶优化”(不看梯度的算法)硬搜。
- 二阶可导 (Twice Differentiability) —— 为了牛顿法
- 如果你想用牛顿法,函数不仅要有坡度(一阶导),还得有“曲率”(二阶导)。
- 这意味着地形不仅要平滑,而且弯曲的程度也要是平滑变化的,不能突变。
- 连续性 (Continuity) —— 路不能断
全局 vs. 局部
- 全局最优 (Global Optimum):整个定义域内最低的点。
- 局部最优 (Local Optimum):在一个小邻域内是最低的,但外面可能有更低的点。
大多数确定性算法(如梯度下降)只能保证找到局部最优。除非,这个函数具有一种特殊的性质——凸性(convex)。
凸函数(Convex Function)
凸函数是优化领域里的“好人”。如果你的优化问题是凸的(Convex Optimization),那么局部最优解 = 全局最优解。这是所有优化工程师梦寐以求的性质。
直观定义
想象一个碗。 如果你在函数图像上任意取两点连一条线段(弦),这条线段上的所有点都在函数图像的上方(或重合),那么它就是凸函数。
数学定义
函数 $f: \mathbb{R}^n \to \mathbb{R}$ 是凸的,当且仅当对于任意 $x, y$ 和任意 $\theta \in [0, 1]$,满足:
$$f(\theta x + (1-\theta)y) \le \theta f(x) + (1-\theta)f(y)$$- 左边 $f(\dots)$:表示我们在 $x$ 和 $y$ 之间找一点,看它的实际高度。
- 右边 $\dots f(\dots)$:表示 $x$ 和 $y$ 的连线(弦)在那一点的高度。
- $\le$ 号:意味着实际高度永远低于或等于弦的高度。
判定方法
一维情况 ($x$ 是实数):看二阶导数 $f''(x)$。如果对于所有的 $x$,都有 $f''(x) \ge 0$,那么它就是凸函数。
- 例子: $f(x) = x^2 \to f''(x) = 2 > 0$ (凸的)。
- 例子: $f(x) = -\log(x) \to f'(x) = -1/x \to f''(x) = 1/x^2 > 0$ (凸的)。
多维情况 ($x$ 是向量):看海森矩阵 (Hessian Matrix, $\nabla^2 f(x)$)。 如果对于所有的 $x$,海森矩阵都是 半正定 (Positive Semidefinite, PSD) 的(即所有特征值 $\ge 0$),那么它就是凸函数。
海森矩阵(Hessian Matrix)
海森矩阵是多元函数的二阶偏导数构成的方阵。它描述了函数的局部曲率(Curvature)。
数学定义:二阶导数的“完全体”
在高中数学里,对于单变量函数 $f(x)$,我们有:
- 一阶导 $f'(x)$:斜率。
- 二阶导 $f''(x)$:曲率(凹凸性)。$f''>0$ 开口向上,$f''<0$ 开口向下。
到了多变量函数 $f(x_1, x_2, \dots, x_n)$,二阶导数就不止一个了,而是一群。我们需要考虑所有变量两两之间的关系。于是我们就把它们排成一个 $n \times n$ 的矩阵,这就是海森矩阵 $\mathbf{H}$ (或者写成 $\nabla^2 f(x)$):
$$\mathbf{H} = \begin{bmatrix} \frac{\partial^2 f}{\partial x_1^2} & \frac{\partial^2 f}{\partial x_1 \partial x_2} & \cdots & \frac{\partial^2 f}{\partial x_1 \partial x_n} \\ \frac{\partial^2 f}{\partial x_2 \partial x_1} & \frac{\partial^2 f}{\partial x_2^2} & \cdots & \frac{\partial^2 f}{\partial x_2 \partial x_n} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial^2 f}{\partial x_n \partial x_1} & \frac{\partial^2 f}{\partial x_n \partial x_2} & \cdots & \frac{\partial^2 f}{\partial x_n^2} \end{bmatrix}$$- 对角线元素 ($\frac{\partial^2 f}{\partial x_i^2}$):表示在第 $i$ 个坐标轴方向上的弯曲程度。
- 非对角线元素 ($\frac{\partial^2 f}{\partial x_i \partial x_j}$):表示变量 $i$ 和变量 $j$ 之间的“纠缠”程度(混合偏导数)。通常情况下,矩阵是对称的(即 $H_{ij} = H_{ji}$)。
海森矩阵通过它的特征值 (Eigenvalues) 告诉我们脚下的地形长什么样。现在,想象你站在一个曲面上:
- 正定矩阵 (所有特征值 > 0):碗底 (Local Minimum)
- 无论你往哪个方向走,地势都是向上弯曲的。
- 这就是凸函数(严格凸)。
- 负定矩阵 (所有特征值 < 0):山顶 (Local Maximum)
- 无论往哪个方向走,地势都是向下弯曲的。
- 不定矩阵 (特征值有正有负):马鞍面 (Saddle Point)
- 往一个方向走是上坡(上凸),往另一个方向走是下坡(下凹)。
- 就像马鞍一样,或者是两座山之间的那个山口。这是优化中最头疼的地方,因为梯度在这里也是 0,很容易骗过算法。
半正定 (Positive Semidefinite, PSD)
可以把它类比为实数中的“非负数”($\ge 0$)。就像我们说一个数是非负的一样,说一个矩阵是“半正定”的,意味着它在某种意义上总是“大于或等于零”的。
核心定义
对于一个 $n \times n$ 的实对称矩阵 $A$,如果对于任意的非零向量 $x$($n$ 维列向量),都有:
$$x^T A x \ge 0$$那么我们就称矩阵 $A$ 是半正定的。这里的 $x^T A x$ 叫做二次型,你可以把它看作是一个能量函数或者地形的高度。
以一个 $2 \times 2$ 矩阵为例子。
$$A = \begin{pmatrix} 2 & 0 \\ 0 & 1 \end{pmatrix}$$几何直觉:看着像什么?
上面提到的二次型 $x^T A x$ 其实就是一个把向量 $x$ 映射成一个实数的函数。如果我们设向量 $x = \begin{pmatrix} u \\ v \end{pmatrix}$,那么:
$$x^T A x = \begin{pmatrix} u & v \end{pmatrix} \begin{pmatrix} 2 & 0 \\ 0 & 1 \end{pmatrix} \begin{pmatrix} u \\ v \end{pmatrix} = 2u^2 + 1v^2$$把 $z = 2u^2 + v^2$ 画在三维坐标系里,它就是一个椭圆抛物面。
- 形状:它像一个两边往上翘的碗。
- 高度:无论你取什么非零的 $(u, v)$,算出来的高度 $z$ 永远是正数。最低点在原点 $(0,0)$,高度为 0。
- 结论:因为所有地方(除了原点)都比 0 高,所以这个矩阵是正定的(当然也属于半正定)。
对比一下: 如果有一个方向是往下弯的(比如马鞍面),那它就不是半正定的。
特征值判定:数字说明了什么?
如果不画图,我们怎么知道这个碗是不是开口朝上呢?这就轮到 特征值 出场了。
对于对角矩阵 $A = \begin{pmatrix} 2 & 0 \\ 0 & 1 \end{pmatrix}$,它的特征值就在对角线上,非常明显:
- $\lambda_1 = 2$
- $\lambda_2 = 1$
判定规则:半正定矩阵的所有特征值都必须 $\ge 0$。(如果是正定矩阵,特征值必须严格 $> 0$)。
那么,为什么特征值能决定形状? 特征值其实代表了抛物面在主轴方向上的弯曲程度(也就是曲率)。
- $\lambda_1 = 2$:表示在 $u$ 轴方向上,碗壁比较陡峭(弯得厉害,向上)。
- $\lambda_2 = 1$:表示在 $v$ 轴方向上,碗壁稍微平缓一点(但也向上)。
只要所有方向都“向上弯”或者“平着”($\ge 0$),整个形状就一定是个“碗”或者“槽”,不会漏底。
如何求解非对角矩阵的特征值
对于非对角矩阵,我们通常使用 **特征方程(Characteristic Equation)**来求解特征值。核心思路是从特征值的定义出发:
$$A\mathbf{v} = \lambda\mathbf{v}$$这里,$A$ 是矩阵,$\mathbf{v}$ 是非零向量(特征向量),$\lambda$ 就是我们要找的特征值。 我们可以把这个等式变形为:
$$(A - \lambda I)\mathbf{v} = \mathbf{0}$$为了让这个方程有非零解(即 $\mathbf{v} \neq \mathbf{0}$),系数矩阵 $(A - \lambda I)$ 的行列式必须等于零。这就得到了我们的通用解法公式:
$$\det(A - \lambda I) = 0$$这里,$I$ 是单位矩阵 (Identity Matrix)。
以求解矩阵 $C = \begin{pmatrix} 1 & 2 \\ 2 & 1 \end{pmatrix}$ 特征值为例。
- 列出特征方程求解特征值的核心公式是:$$\det(C - \lambda I) = 0$$
- 代入矩阵将矩阵 $C$ 和单位矩阵 $I$ 代入公式。$$C - \lambda I = \begin{pmatrix} 1 & 2 \\ 2 & 1 \end{pmatrix} - \lambda \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} = \begin{pmatrix} 1-\lambda & 2 \\ 2 & 1-\lambda \end{pmatrix}$$
- 计算行列式对于 $2 \times 2$ 矩阵 $\begin{pmatrix} a & b \\ c & d \end{pmatrix}$,行列式是 $ad - bc$。这里 $a = 1-\lambda, d = 1-\lambda, b = 2, c = 2$。$$\det(C - \lambda I) = (1-\lambda)(1-\lambda) - (2 \times 2)$$
- 展开并化简方程展开上面的式子:$$(1 - 2\lambda + \lambda^2) - 4 = 0$$ $$\lambda^2 - 2\lambda - 3 = 0$$这就是这个矩阵的特征多项式。
- 求解一元二次方程我们要解方程 $\lambda^2 - 2\lambda - 3 = 0$。可以通过因式分解来做:我们要找两个数,乘积是 -3,和是 -2。这两个数是 -3 和 +1。$$(\lambda - 3)(\lambda + 1) = 0$$或者使用求根公式 $\lambda = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$:$$\lambda = \frac{2 \pm \sqrt{(-2)^2 - 4(1)(-3)}}{2} = \frac{2 \pm \sqrt{4 + 12}}{2} = \frac{2 \pm 4}{2}$$
- 最终结果解得两个特征值为:$\lambda_1 = \frac{2+4}{2} = 3, \lambda_2 = \frac{2-4}{2} = -1$
结论:矩阵 $C$ 的特征值是 3 和 -1。
import numpy as np
import matplotlib.pyplot as plt
# 1. 设置 x 和 y 的网格范围
x = np.linspace(-3, 3, 50)
y = np.linspace(-3, 3, 50)
X, Y = np.meshgrid(x, y)
# 2. 定义两个二次型函数
# 例子 1: 正定矩阵 A = [[2, 0], [0, 1]]
# z = 2x^2 + 1y^2
Z_positive = 2 * X**2 + 1 * Y**2
# 例子 2: 不定矩阵 B = [[1, 0], [0, -3]]
# z = 1x^2 - 3y^2
Z_indefinite = 1 * X**2 - 3 * Y**2
# 3. 创建绘图
fig = plt.figure(figsize=(14, 6))
# --- 绘制第一个图 (碗) ---
ax1 = fig.add_subplot(1, 2, 1, projection='3d')
ax1.plot_surface(X, Y, Z_positive, cmap='viridis', alpha=0.8, edgecolor='none')
ax1.set_title('Positive Definite (Bowl)\nEigenvalues: 2, 1')
ax1.set_xlabel('X axis')
ax1.set_ylabel('Y axis')
ax1.set_zlabel('Z value')
ax1.scatter(0, 0, 0, color='red', s=50, label='Global Min') # 标记最低点
# --- 绘制第二个图 (马鞍) ---
ax2 = fig.add_subplot(1, 2, 2, projection='3d')
ax2.plot_surface(X, Y, Z_indefinite, cmap='coolwarm', alpha=0.8, edgecolor='none')
ax2.set_title('Indefinite (Saddle)\nEigenvalues: 1, -3')
ax2.set_xlabel('X axis')
ax2.set_ylabel('Y axis')
ax2.set_zlabel('Z value')
ax2.scatter(0, 0, 0, color='green', s=50, label='Saddle Point') # 标记鞍点
plt.tight_layout()
plt.show()
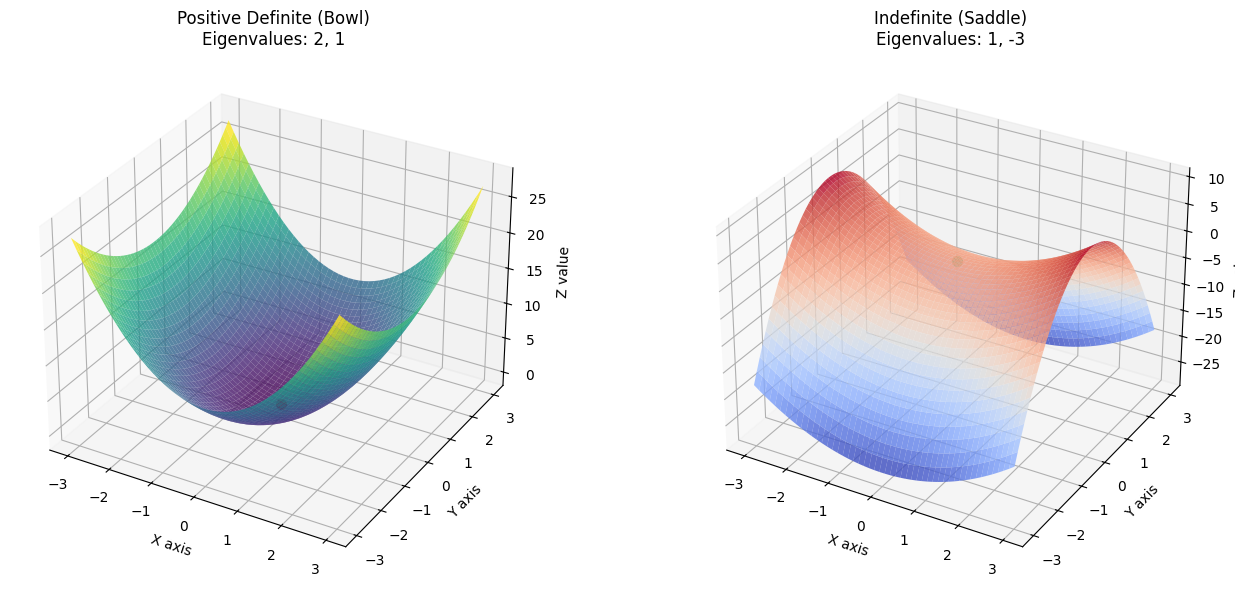
留意上图中的原点 $(0,0)$:
- 在 左图(碗) 中,如果你放一个小球在任意位置,它最终都会滚落到红色的最低点。
- 在 右图(马鞍) 中,如果你从 $X$ 轴方向走,那是上坡;但如果你从 $Y$ 轴方向走,那就是下坡。
牛顿法(Newton’s Method)
适用于 1 维
牛顿法是一种 二阶优化算法。
- 一阶算法(如梯度下降): 只利用梯度(坡度/斜率)信息,告诉我们往哪走会让函数值下降。
- 二阶算法(如牛顿法): 不仅利用梯度,还利用 二阶导数(曲率) 信息。它不仅知道坡有多陡,还知道坡的弯曲程度。
核心思想:二次近似 (Quadratic Approximation)**
牛顿法的核心逻辑是:用一个二次函数(抛物线/抛物面)去拟合当前位置的曲线,然后直接跳到这个抛物面的最低点。
步骤 1:二阶泰勒展开 (拟合)
我们在当前点 $x_k$ 附近,把复杂的目标函数 $f(x)$ 展开成一个二次多项式:
$$f(x) \approx f(x_k) + \nabla f(x_k)^T (x - x_k) + \frac{1}{2} (x - x_k)^T \mathbf{H}(x_k) (x - x_k)$$- 第一部分是平面(梯度)。
- 第二部分是弯曲(海森矩阵)。
步骤 2:求导找极值 (跳跃)
我们想找到这个近似抛物面的最低点。这就很简单了,对上面的式子求导,并令导数为 0:
$$\nabla f(x_k) + \mathbf{H}(x_k)(x - x_k) = 0$$步骤 3:得出更新公式
解上面的方程,把 $x$ 算出来,就是我们要去的下一个点 $x_{k+1}$:
$$\mathbf{x}_{k+1} = \mathbf{x}_k - \mathbf{H}^{-1}(x_k) \nabla f(x_k)$$这就是牛顿法的迭代公式。看,它比梯度下降多乘了一个 $\mathbf{H}^{-1}$(海森矩阵的逆)。
更新停止准则 (Stopping Criteria)
梯度判定:坡度变平了吗?
- 这是理论上最过硬的标准。最优点的必要条件是梯度为 0。
- 准则:当梯度的范数 (Norm) 小于某个阈值(比如 $10^{-6}$)时停止。
- 数学公式:$$||\nabla f(x_k)|| < \epsilon$$
- 直觉:如果你脚下的地已经平得像飞机场一样(坡度几乎没有了),那你大概率已经在谷底了。
步长判定:还在移动吗?
- 有时候梯度计算很贵,或者地形非常平坦,我们可以看 $x$ 的变化量。
- 准则:如果这一步更新的位置 $x_{k+1}$ 和上一步 $x_k$ 几乎重合,说明算法已经走不动了。
- 数学公式:$$||x_{k+1} - x_k|| < \epsilon$$
- 直觉:如果你迈一步只能前进 0.000001 毫米,那继续走的意义不大了。
函数值判定:收益还明显吗?
- 这是从“性价比”角度考虑。
- 准则:如果目标函数的值 $f(x)$ 几乎不再下降。
- 数学公式:$$|f(x_{k+1}) - f(x_k)| < \epsilon$$
- 直觉:如果折腾了一大顿,成本只降低了 1 分钱,这时候通常就会叫停(Diminishing returns)。
预算判定(强制):时间到了吗?
- 这是为了防止死循环或计算超时。
- 准则:达到预设的最大迭代次数 (Max Iterations)。
- 直觉:老板只给了 1000 块钱(计算资源),不管有没有找到最好的解,钱花完就得停。
优缺点
- ✅ 极速收敛:通常几步就能走到谷底(二次收敛速度)。
- ❌ 计算代价极高:计算海森矩阵 $\mathbf{H}$ 的逆矩阵需要 $O(n^3)$ 的复杂度。在高维问题中($n$ 很大)几乎不可用。因此,一般我们将其用在一维问题上。
- ❌ 对初值敏感:如果初始点离最优解太远,且函数非凸,牛顿法可能会飞到外太空去。
示例
示例一:手算
目标函数:$f(x) = x^2 - 4x + 4$ (这是一个开口向上的抛物线,最小值显然在 $x=2$)。
假设我们从 $x_0 = 10$ 这个很远的地方开始。
- 计算梯度 (一阶导):$g(x) = f'(x) = 2x - 4$在 $x_0=10$ 处,$g(10) = 2(10) - 4 = 16$。
- 计算海森 (二阶导):$h(x) = f''(x) = 2$注意:这里的二阶导是一个常数 $2$(这说明原函数本身就是个标准的二次函数)。
- 牛顿法更新:公式:$x_{new} = x_{old} - \frac{g(x)}{h(x)}$$$x_1 = 10 - \frac{16}{2} = 10 - 8 = 2$$
- 确定 $x=2$ 是不是最优值
- 方法一:验算梯度(最硬核的标准)
- 这是最直接的数学判断。最优点的定义就是 “斜率为 0 的点”。只要我们算出新位置的梯度(一阶导数)是 0,就说明我们到了一个平坦的地方(极值点)
- 。回顾我们的函数:$f'(x) = 2x - 4$
- 代入结果 $x=2$:$$f'(2) = 2(2) - 4 = 4 - 4 = 0$$
- ✅ 验证成功:斜率为 0,说明我们确实站在了谷底(或者山顶/鞍点)。
- 方法二:验算二阶导数(确认是谷底)
- 梯度为 0 也有可能是山顶(最大值)。要确定是最小值,我们要看海森(二阶导)。
- 回顾:$f''(x) = 2$
- 判断:$2 > 0$(正数)。
- 尝试“再走一步”(算法视角的验证)
- 可以告诉算法:“你在 $x=2$ 这个位置,再给我做一次牛顿法更新!”来看看会发生什么:
- 当前位置:$x_{old} = 2$
- 当前梯度:$g(2) = 0$
- 当前二阶导:$h(2) = 2$
- 牛顿法公式:$$x_{new} = x_{old} - \frac{g(x_{old})}{h(x_{old})} = 2 - \frac{0}{2} = 2 - 0 = 2$$
- ✅ 验证成功:算法走不动了。无论你让它再跑 100 轮,它都会死死钉在 $x=2$ 这个位置。这意味着收敛(Convergence)。
- 可以告诉算法:“你在 $x=2$ 这个位置,再给我做一次牛顿法更新!”来看看会发生什么:
- 方法一:验算梯度(最硬核的标准)
结果:惊不惊喜?只用了一步,我们就从 $10$ 直接跳到了 $2$(也就是全局最优解)。
示例二
这个例子让你直观地感受到牛顿法 (Newton’s Method) 的威力,特别是它的二阶收敛速度和停止准则。这里特意选择了一个非二次函数:
$$f(x, y) = x^4 + y^4$$import numpy as np
import matplotlib.pyplot as plt
# --- 1. 定义目标函数、梯度、海森矩阵 ---
# 目标函数: f(x, y) = x^4 + y^4 (最小值在 0,0)
def func(p):
x, y = p
return x**4 + y**4
# 一阶导数 (梯度 Gradient): [4x^3, 4y^3]
def gradient(p):
x, y = p
return np.array([4 * x**3, 4 * y**3])
# 二阶导数 (海森矩阵 Hessian): [[12x^2, 0], [0, 12y^2]]
def hessian(p):
x, y = p
return np.array([[12 * x**2, 0],
[0, 12 * y**2]])
# --- 2. 牛顿法核心算法 ---
def newton_optimization(start_point, tolerance=1e-6, max_iter=100):
path = [start_point]
x = np.array(start_point, dtype=float)
print(f"{'Iter':<5} | {'x':<20} | {'Grad Norm':<15}")
print("-" * 45)
for i in range(max_iter):
g = gradient(x)
H = hessian(x)
# --- 停止准则 1: 梯度足够小吗? ---
grad_norm = np.linalg.norm(g)
print(f"{i:<5} | {str(x):<20} | {grad_norm:.8f}")
if grad_norm < tolerance:
print(f"\n✅ 达到停止准则: 梯度范数 {grad_norm:.2e} < {tolerance}")
break
# --- 牛顿法更新 ---
# 公式: x_new = x - H^-1 * g
# 工程技巧: 尽量不要直接求逆矩阵 (inv),解线性方程组 (solve) 更快更稳
# H * step = g => step = H^-1 * g
try:
step = np.linalg.solve(H, g)
except np.linalg.LinAlgError:
print("⚠️ 海森矩阵不可逆(可能是奇异矩阵),停止迭代。")
break
x = x - step
path.append(x)
return np.array(path)
# --- 3. 运行算法 ---
start_pos = [2.0, 2.5] # 从 (2, 2.5) 开始
path_newton = newton_optimization(start_pos)
# --- 4. 可视化结果 ---
x_grid = np.linspace(-3, 3, 100)
y_grid = np.linspace(-3, 3, 100)
X, Y = np.meshgrid(x_grid, y_grid)
Z = X**4 + Y**4
plt.figure(figsize=(8, 7))
plt.contour(X, Y, Z, levels=30, cmap='gray_r', alpha=0.4) # 画等高线
plt.plot(path_newton[:, 0], path_newton[:, 1], 'o-', color='red', lw=2, label="Newton's Path")
# 标记起点和终点
plt.scatter(path_newton[0,0], path_newton[0,1], color='blue', s=100, label='Start')
plt.scatter(path_newton[-1,0], path_newton[-1,1], color='green', marker='*', s=200, zorder=5, label='Converged')
plt.title(f"Newton's Method Optimization on $f(x,y) = x^4 + y^4$")
plt.legend()
plt.grid(True, linestyle='--')
plt.show()
Iter | x | Grad Norm
---------------------------------------------
0 | [2. 2.5] | 70.21573898
1 | [1.33333333 1.66666667] | 20.80466340
2 | [0.88888889 1.11111111] | 6.16434471
3 | [0.59259259 0.74074074] | 1.82647251
4 | [0.39506173 0.49382716] | 0.54117704
5 | [0.26337449 0.32921811] | 0.16034875
6 | [0.17558299 0.21947874] | 0.04751074
7 | [0.11705533 0.14631916] | 0.01407726
8 | [0.07803688 0.09754611] | 0.00417104
9 | [0.05202459 0.06503074] | 0.00123586
10 | [0.03468306 0.04335382] | 0.00036618
11 | [0.02312204 0.02890255] | 0.00010850
12 | [0.01541469 0.01926837] | 0.00003215
13 | [0.01027646 0.01284558] | 0.00000953
14 | [0.00685097 0.00856372] | 0.00000282
15 | [0.00456732 0.00570915] | 0.00000084
✅ 达到停止准则: 梯度范数 8.36e-07 < 1e-06
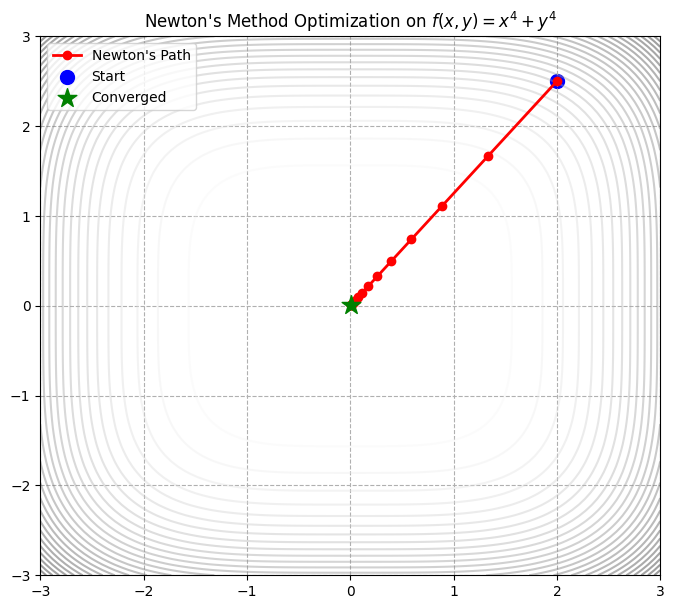
代码解析 (Highlights)
- 收敛速度:
- 你可以看到打印出来的 Grad Norm。注意看它下降的速度。
- 一开始可能比较慢,但一旦接近谷底,梯度范数会呈现断崖式下跌(比如从 0.1 直接变 0.0001)。这就是二次收敛的特征。
np.linalg.solve(H, g):- 虽然数学公式写的是 $\mathbf{H}^{-1} \mathbf{g}$,但在写代码时,永远不要调用
inv()(求逆) 除非万不得已。 - 解线性方程组 $Ax=b$ 比求 $A^{-1}$ 效率更高,数值误差更小。
- 虽然数学公式写的是 $\mathbf{H}^{-1} \mathbf{g}$,但在写代码时,永远不要调用
- 停止准则:
- 代码中用
grad_norm < tolerance作为一个硬性指标。你可以试着把 start_pos 改远一点,看看它需要多少步。
- 代码中用
坐标下降法(Simple Relaxation)
适用于 N 维
在连续优化算法的语境下,这通常指的是 Coordinate Descent (坐标下降法),或者在线性方程组求解中的 Gauss-Seidel 方法。这其实就是 Gibbs Sampling 的确定性版本!
坐标下降法是一种 “分而治之” 的策略。
- 牛顿法/梯度下降:是“全军出击”。每次更新时,所有变量 $(x_1, x_2, \dots, x_n)$ 一起动,沿着合力的方向走。
- 坐标下降 (Relaxation):是“单兵作战”。每次只允许一个变量动,其他变量全部被锁死(视为常数)。
几何直觉:想象你在一个城市里(曼哈顿),你只能沿着东西向(X轴)或者南北向(Y轴)的街道走,不能走斜线。你要去城市的最低点,只能先往东走一段,停下来,再往南走一段,如此循环。
算法流程(分而治之)
假设我们要最小化 $f(x_1, x_2, \dots, x_n)$。
- 初始化:随便选个起点 $x^{(0)}$。
- 循环(直到收敛):
- 更新 $x_1$:固定 $x_2, \dots, x_n$,找一个 $x_1$ 让 $f$ 最小。$$x_1^{(new)} = \underset{x_1}{\text{argmin}} \ f(x_1, x_2^{(old)}, \dots, x_n^{(old)})$$
- 此时 $f$ 退化成一个一维函数,我们就可以利用导数(例如牛顿法)来求解最小值了。
- 更新 $x_2$:固定 $x_1^{(new)}, x_3, \dots, x_n$,找一个 $x_2$ 让 $f$ 最小。
- …
- 更新 $x_n$:固定前面所有新的,找 $x_n$。
- 更新 $x_1$:固定 $x_2, \dots, x_n$,找一个 $x_1$ 让 $f$ 最小。$$x_1^{(new)} = \underset{x_1}{\text{argmin}} \ f(x_1, x_2^{(old)}, \dots, x_n^{(old)})$$
核心逻辑:每次只解决一个一维优化问题。
优缺点
优点
- 无需梯度:如果单变量优化很容易解(比如有解析解),你甚至不需要算梯度。
- 曼哈顿移动:轨迹是锯齿状(Zig-zag)的,只能沿着坐标轴走。
- 适用性:非常适合变量之间耦合度低,或者有 L1 正则化(Lasso)的情况。
缺点
- 变量强相关时极慢。想象一个斜向摆放的狭长山谷(变量 $x$ 和 $y$ 高度相关,比如 $f = (x-y)^2$),坐标下降法会非常痛苦。它想往谷底走,但因为不能走斜线,只能在两壁之间疯狂撞墙,每一步都只能前进一点点。
示例
基础示例
目标函数:$f(x, y) = x^2 + xy + y^2$这是一维碗状函数,但是 $xy$ 这一项让它的等高线变成了斜椭圆。
手动推导更新公式(为了代码写得快):
- 针对 $x$ 优化:把 $y$ 当常数。$f$ 对 $x$ 求导 $= 2x + y = 0 \implies x = -y/2$。
- 针对 $y$ 优化:把 $x$ 当常数。$f$ 对 $y$ 求导 $= x + 2y = 0 \implies y = -x/2$。
import numpy as np
import matplotlib.pyplot as plt
# 目标函数: f(x,y) = x^2 + xy + y^2
def func(p):
x, y = p
return x**2 + x*y + y**2
# --- 坐标下降法 (Simple Relaxation) ---
def coordinate_descent(start_point, n_cycles=10):
path = [start_point]
x, y = start_point
print(f"{'Step':<5} | {'x':<10} | {'y':<10} | {'Action'}")
print("-" * 45)
for i in range(n_cycles):
# 1. 固定 y, 优化 x
# 导数 2x + y = 0 => x = -y / 2
x_new = -y / 2
path.append([x_new, y]) # 记录路径
print(f"{i*2+1:<5} | {x_new:<10.4f} | {y:<10.4f} | Update x")
x = x_new # 更新当前x
# 2. 固定 x, 优化 y
# 导数 x + 2y = 0 => y = -x / 2
y_new = -x / 2
path.append([x, y_new]) # 记录路径
print(f"{i*2+2:<5} | {x:<10.4f} | {y_new:<10.4f} | Update y")
y = y_new # 更新当前y
return np.array(path)
# --- 运行 ---
start_pos = [2.0, 2.0]
path_cd = coordinate_descent(start_pos, n_cycles=5)
# --- 可视化 ---
x_grid = np.linspace(-2.5, 2.5, 100)
y_grid = np.linspace(-2.5, 2.5, 100)
X, Y = np.meshgrid(x_grid, y_grid)
Z = X**2 + X*Y + Y**2
plt.figure(figsize=(8, 7))
plt.contour(X, Y, Z, levels=20, cmap='viridis', alpha=0.5)
# 画出锯齿状路径
plt.plot(path_cd[:, 0], path_cd[:, 1], 'o-', color='red', lw=2, label="Coordinate Descent Path")
plt.scatter(0, 0, marker='*', s=200, color='gold', zorder=5, label="Global Min")
plt.title("Simple Relaxation (Coordinate Descent) on $x^2 + xy + y^2$")
plt.legend()
plt.grid(True, linestyle='--')
plt.show()
Step | x | y | Action
---------------------------------------------
1 | -1.0000 | 2.0000 | Update x
2 | -1.0000 | 0.5000 | Update y
3 | -0.2500 | 0.5000 | Update x
4 | -0.2500 | 0.1250 | Update y
5 | -0.0625 | 0.1250 | Update x
6 | -0.0625 | 0.0312 | Update y
7 | -0.0156 | 0.0312 | Update x
8 | -0.0156 | 0.0078 | Update y
9 | -0.0039 | 0.0078 | Update x
10 | -0.0039 | 0.0020 | Update y
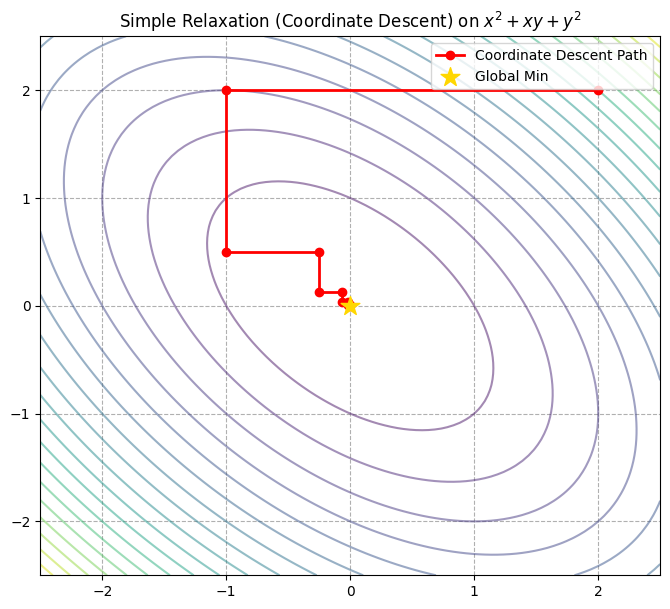
看上图:
- 直角转弯:你会发现路径完全由水平线和垂直线组成。这就是“曼哈顿距离”式的移动。
- 收敛:虽然每一步都是精准的(直接跳到当前维度最小值),但由于 $x$ 和 $y$ 互相牵制($xy$ 那个耦合项),它不能直接跳到原点,而是像走楼梯一样慢慢旋进去。
- 对比:如果是牛顿法,对于这个二次函数,它依然是一步就跳到原点 $(0,0)$。但牛顿法需要算矩阵逆,而这里我们只需要做除法
/2。
示例:变量强相关时极慢
场景设定:狭窄的斜谷 (The Narrow Diagonal Valley)
想象地形是一个非常狭窄、且斜着摆放的山谷。
- 谷底是一条斜线(比如 $y \approx -x$)。
- 要想走到最低点,你必须同时调整 $x$ 和 $y$(即走斜线)。
但坐标下降法是个“强迫症患者”,它每次只能动一个坐标:
- 它想往左下走,但只能先往左挪一点点,然后撞到了谷壁(函数值变高)。
- 它只好停下来,改为往下挪一点点,又撞到了谷壁。
- 于是它只能在两堵墙之间疯狂弹球,步长变得极短,仿佛在原地踏步。
数学构造
我们把上一个例子里的耦合项 $xy$ 的系数加大。上个例子是 $x^2 + xy + y^2$(系数 1),这次我们改成 1.9(接近 2)。
$$f(x, y) = x^2 + \mathbf{1.9}xy + y^2$$- 当这个中间系数接近 2 时,等高线会被压得极其扁平。
- 更新公式变化:
- 对 $x$ 求导 $= 2x + 1.9y = 0 \implies x = -0.95y$
- 对 $y$ 求导 $= 1.9x + 2y = 0 \implies y = -0.95x$
你看,每次更新,$x$ 只是变成了 $y$ 的 -0.95 倍。这意味着每次迭代,数值只缩小了 5%。这是一个极其缓慢的收敛过程。
import numpy as np
import matplotlib.pyplot as plt
# 这是一个"病态"函数,变量高度耦合
def func(p):
x, y = p
# 系数 1.9 让椭圆变得极其狭长
return x**2 + 1.9 * x * y + y**2
# --- 坐标下降法 ---
def coordinate_descent_bad_case(start_point, n_cycles=10):
path = [start_point]
x, y = start_point
for i in range(n_cycles):
# 1. Update x: 2x + 1.9y = 0 => x = -0.95y
x = -0.95 * y
path.append([x, y])
# 2. Update y: 1.9x + 2y = 0 => y = -0.95x
y = -0.95 * x
path.append([x, y])
return np.array(path)
# --- 运行对比 ---
start_pos = [4.0, 3.0] # 从远一点开始
# 我们跑个 20 轮,看看它能走多远
path_cd = coordinate_descent_bad_case(start_pos, n_cycles=20)
# --- 可视化 ---
x_grid = np.linspace(-5, 5, 100)
y_grid = np.linspace(-5, 5, 100)
X, Y = np.meshgrid(x_grid, y_grid)
Z = X**2 + 1.9*X*Y + Y**2
plt.figure(figsize=(10, 8))
# 画出非常扁平的等高线
plt.contour(X, Y, Z, levels=np.logspace(-1, 2, 20), cmap='magma', alpha=0.5)
# 画路径
plt.plot(path_cd[:, 0], path_cd[:, 1], '.-', color='red', lw=1, markersize=4, label="Coordinate Descent Path")
plt.scatter(0, 0, marker='*', s=200, color='gold', zorder=5, label="Global Min")
plt.scatter(start_pos[0], start_pos[1], color='blue', label='Start')
plt.title("The Weakness: Zig-zagging in a Narrow Valley\n$f(x,y) = x^2 + 1.9xy + y^2$")
plt.legend()
plt.grid(True, linestyle='--')
plt.show()
# 打印最后几步的值看看有没有到原点
print(f"Start: {start_pos}")
print(f"End (after 40 steps): {path_cd[-1]}")
print(f"True Min: [0, 0]")
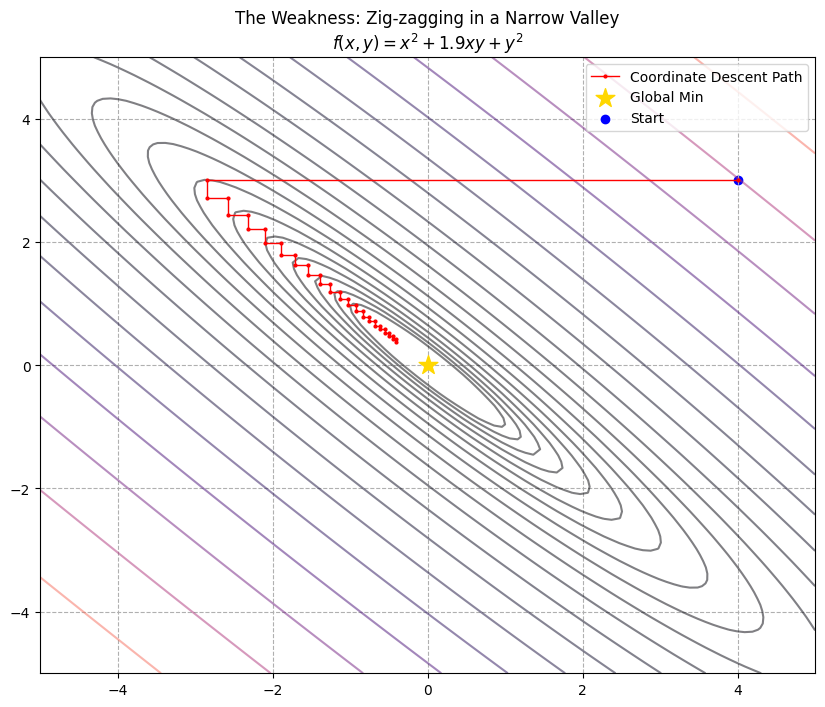
Start: [4.0, 3.0]
End (after 40 steps): [-0.40582786 0.38553647]
True Min: [0, 0]
上图是一张非常有冲击力的图:
- “缝纫机"效应:路径变成了密密麻麻的红色折线,像缝纫机的针脚一样紧密。
- 原地踏步:虽然我们跑了 20 轮(40 步更新),但你可以看打印出来的 End 坐标。它离原点 $(0,0)$ 可能还有很长一段距离。而在上一个例子里,5 轮就差不多到了。
- 直觉理解:这就好比你要把一个很宽的沙发搬进一个很窄的走廊。
- 如果是梯度下降(或者人搬沙发),我们会把沙发斜过来,顺着走廊的方向直接推过去。
- 坐标下降法就像是一个只能横着走或竖着走的机器人。它只能把沙发往左蹭 1 厘米,碰壁了;再往下蹭 1 厘米,又碰壁了。如此循环,效率极其低下。
最速下降法(Steepest Descent)
适用于 N 维
Steepest Descent 是一种 一阶优化算法。
- 直觉:想象你在山上,眼睛蒙着布。为了尽快下山,你用脚探一探四周,感觉到哪个方向向下倾斜得最厉害,你就往那个方向迈一步。
- 数学核心:
- 梯度 ($\nabla f$):指向函数增长最快(上坡最陡)的方向。
- 负梯度 ($-\nabla f$):指向函数下降最快(下坡最陡)的方向。
- 对比:
- 它不像 Coordinate Descent 那样只能走直角,它可以走任意方向。
- 它不像 Newton’s Method 那样能看到地形弯曲,它是个“近视眼”,只看脚下的坡度。
核心思想:贪婪下坡
我们在当前位置,环顾四周,寻找下坡最陡的方向。数学告诉我们,梯度的方向 $\nabla f(x)$ 是上坡最陡的,所以负梯度方向 $-\nabla f(x)$ 就是下坡最陡的。
所以核心公式非常简单,只有一步:
$$x_{k+1} = x_k - \alpha \nabla f(x_k)$$这里有两个关键角色:
- 方向 ($\nabla f(x_k)$):告诉我们要往哪里走。
- 步长 ($\alpha$, Learning Rate):告诉我们这一步迈多大。
在最古典的“最速下降法”定义中,$\alpha$ 是通过 线性搜索 (Line Search) 确定的(即在这个方向上走多远能让函数值降得最低,我就走多远)。但在现代机器学习中,我们通常把 $\alpha$ 设为一个固定的超参数。
步长 $\alpha$ 的选择 (Line Search)
在最简单的梯度下降中,$\alpha$ 是个常数。但在严谨的 “Steepest Descent” 定义中,我们通常需要进行 线性搜索 (Line Search) 来决定这一步走多远:
$$\alpha_k = \underset{\alpha > 0}{\text{argmin}} \ f(x_k - \alpha \nabla f(x_k))$$即:确定了方向后,我要在这个方向上走到最低点,然后再换方向。
优缺点
- 计算成本:低。算一次梯度很快。
- 路径形态:垂直锯齿 (Zig-zag)。
- 收敛速度:线性收敛 (Linear)。不快不慢。
- 致命弱点:对步长敏感 & 峡谷震荡。
“锯齿” 现象 (Zig-Zagging)
Steepest Descent 有一个著名的弱点。当它使用 精确线性搜索 时,相邻的两次迭代方向是正交(垂直)的。如果地形是一个狭长的椭圆峡谷,这种正交性会导致算法在峡谷两壁之间来回震荡,前进极其缓慢。这也正是为什么我们需要 Momentum(动量)等改进方法的原因。
示例
基础示例
为了展示 Steepest Descent 的特性,我们依然选用那个让坐标下降法头疼的狭长山谷类型的函数:
$$f(x, y) = x^2 + 10y^2$$注意:$y$ 方向的坡度是 $x$ 方向的 10 倍,这就是所谓的条件数差 (Ill-conditioned)。
import numpy as np
import matplotlib.pyplot as plt
# 目标函数: f(x,y) = x^2 + 10y^2
# 这是一个被拉长的椭圆碗
def func(p):
x, y = p
return x**2 + 10 * y**2
# 梯度: [2x, 20y]
def gradient(p):
x, y = p
return np.array([2 * x, 20 * y])
# --- Steepest Descent 算法 ---
def steepest_descent(start_point, learning_rate, n_iter=20):
path = [start_point]
p = np.array(start_point)
for _ in range(n_iter):
grad = gradient(p)
# 核心公式: p_new = p - lr * grad
p = p - learning_rate * grad
path.append(p)
return np.array(path)
# --- 运行对比 ---
start_pos = [8.0, 2.0]
# 1. 步长适中 (0.05)
path_good = steepest_descent(start_pos, learning_rate=0.05, n_iter=20)
# 2. 步长偏大 (0.09) - 接近震荡边缘
path_oscillate = steepest_descent(start_pos, learning_rate=0.09, n_iter=20)
# --- 可视化 ---
x_grid = np.linspace(-10, 10, 100)
y_grid = np.linspace(-4, 4, 100) # Y轴范围小一点,因为它是狭窄方向
X, Y = np.meshgrid(x_grid, y_grid)
Z = X**2 + 10*Y**2
plt.figure(figsize=(12, 6))
# 左图: 正常步长
plt.subplot(1, 2, 1)
plt.contour(X, Y, Z, levels=20, cmap='viridis', alpha=0.5)
plt.plot(path_good[:, 0], path_good[:, 1], 'o-', color='blue', label='LR=0.05')
plt.title("Good Learning Rate\n(Steady Descent)")
plt.legend()
plt.grid(True, linestyle='--')
# 右图: 震荡步长
plt.subplot(1, 2, 2)
plt.contour(X, Y, Z, levels=20, cmap='viridis', alpha=0.5)
plt.plot(path_oscillate[:, 0], path_oscillate[:, 1], 'o-', color='red', label='LR=0.09')
plt.title("Large Learning Rate\n(Zig-zag / Oscillation)")
plt.legend()
plt.grid(True, linestyle='--')
plt.show()
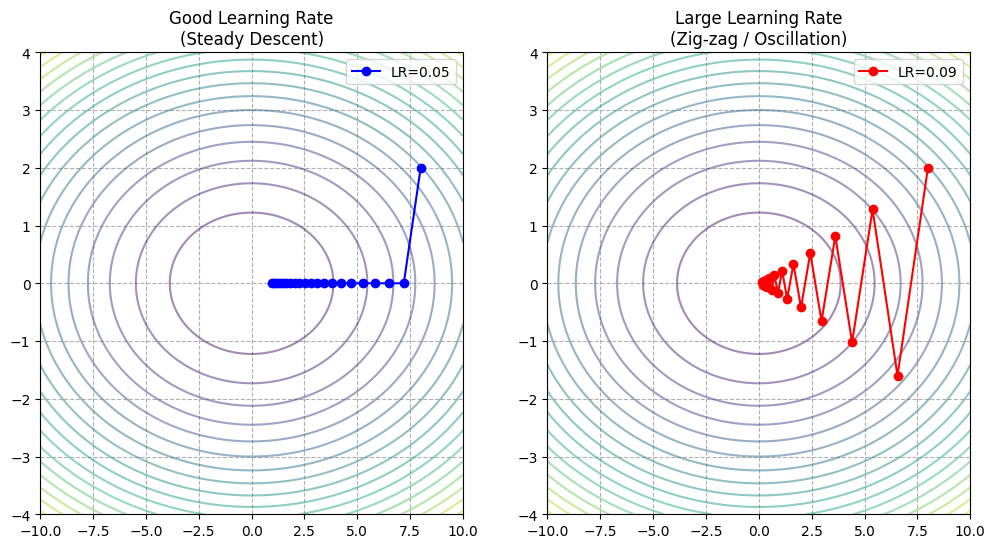
- 左图 (Good LR):
- 虽然它走了斜线,但你发现它并不是直奔圆心(最低点)。
- 因为它先要把陡峭方向 ($y$) 的高度降下来,然后再慢慢搞定平缓方向 ($x$)。
- 它的路径是弯曲的。
- 右图 (Large LR - 震荡):
- 请看红色的线。它在 $y$ 轴方向(陡峭方向)疯狂地跳来跳去。
- 它从峡谷的北壁直接跳到了南壁,又跳回北壁。
- 虽然它在 $x$ 轴方向上确实在慢慢前进,但大量的能量被浪费在了 $y$ 轴的反复横跳上。
- 这就是 Steepest Descent 最大的痛点:面对不同方向坡度差异大的地形(Ill-conditioned),它非常容易震荡,收敛变慢。
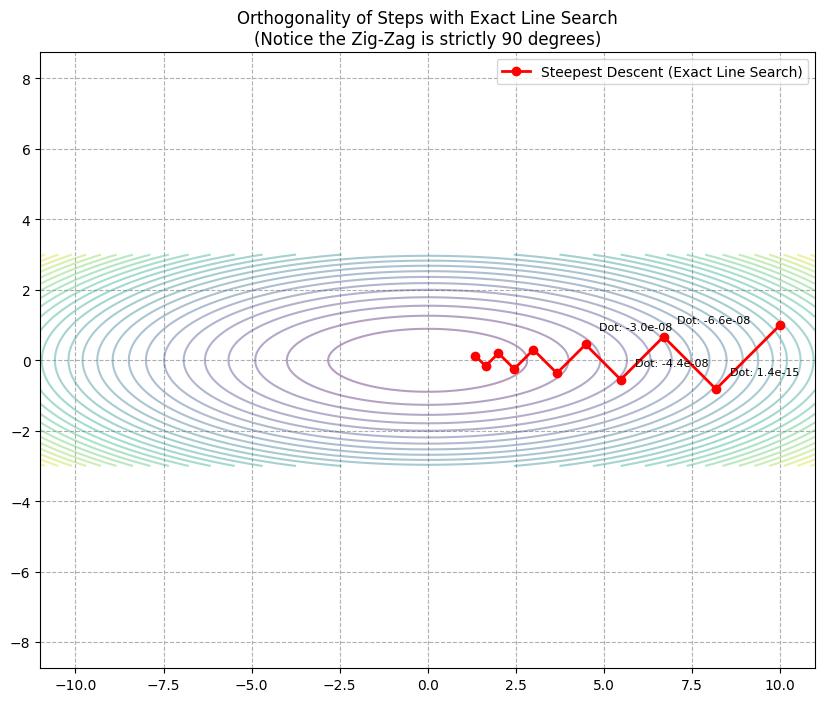
示例:精确线性搜索
只有当使用“精确线性搜索 (Exact Line Search)”来确定步长时,相邻的两次迭代路径才会严格垂直。
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import minimize_scalar
# 目标函数: f(x,y) = x^2 + 10y^2
def func(p):
x, y = p
return x**2 + 10 * y**2
# 梯度
def gradient(p):
x, y = p
return np.array([2 * x, 20 * y])
# --- 带有精确线性搜索的最速下降法 ---
def steepest_descent_exact_line_search(start_point, n_iter=10):
path = [start_point]
x_k = np.array(start_point)
for _ in range(n_iter):
grad = gradient(x_k)
# 定义一个关于 alpha (步长) 的一元函数
# 我们要找到 alpha 使得 f(x_k - alpha * grad) 最小
def line_obj(alpha):
return func(x_k - alpha * grad)
# 使用优化算法找到在这个方向上的最优 alpha
res = minimize_scalar(line_obj)
best_alpha = res.x
# 更新位置
x_new = x_k - best_alpha * grad
path.append(x_new)
# 检查是否收敛(避免除零错误)
if np.linalg.norm(x_new - x_k) < 1e-6:
break
x_k = x_new
return np.array(path)
# --- 运行 ---
start_pos = [10.0, 1.0] # 选一个容易观察的角度
path_exact = steepest_descent_exact_line_search(start_pos, n_iter=10)
# --- 可视化 ---
x_grid = np.linspace(-11, 11, 100)
y_grid = np.linspace(-3, 3, 100)
X, Y = np.meshgrid(x_grid, y_grid)
Z = X**2 + 10*Y**2
plt.figure(figsize=(10, 8))
plt.contour(X, Y, Z, levels=30, cmap='viridis', alpha=0.4)
# 画路径
plt.plot(path_exact[:, 0], path_exact[:, 1], 'o-', color='red', lw=2, label='Steepest Descent (Exact Line Search)')
# 标注直角
for i in range(len(path_exact)-2):
p1 = path_exact[i]
p2 = path_exact[i+1]
p3 = path_exact[i+2]
# 计算向量
v1 = p2 - p1
v2 = p3 - p2
# 验证点积是否为 0 (即垂直)
dot_product = np.dot(v1, v2)
# 为了显示直观,我们只标注前几个明显的转角
if i < 4:
plt.annotate(f"Dot: {dot_product:.1e}", xy=p2, xytext=(10, 10), textcoords='offset points', fontsize=8)
plt.title("Orthogonality of Steps with Exact Line Search\n(Notice the Zig-Zag is strictly 90 degrees)")
plt.axis('equal') # 这一步很关键!如果不设为 equal,坐标轴比例不同,直角看起来就不像直角了
plt.legend()
plt.grid(True, linestyle='--')
plt.show()
示例:三个算法大比拼
把这三个算法放在同一个“竞技场”里,理解它们性格差异的最好方式。为了让比赛更精彩,我们选择一个 **“既有偏斜、又有耦合”**的地形:
$$f(x, y) = x^2 + 1.5xy + 2y^2$$地形分析:这是一个椭圆碗,但是它是斜着放的(因为有 $1.5xy$ 这个耦合项)。
- 这对 Coordinate Descent 是噩梦:因为不能走斜线,它必须画无数个直角楼梯。
- 这对 Steepest Descent 是挑战:因为它容易震荡。
- 这对 Newton’s Method 是送分题:因为它是二次面,牛顿法应该能一眼看穿底牌,一步到位。
import numpy as np
import matplotlib.pyplot as plt
# --- 1. 定义竞技场 (目标函数) ---
# f(x, y) = x^2 + 1.5xy + 2y^2
def func(p):
x, y = p
return x**2 + 1.5*x*y + 2*y**2
def gradient(p):
x, y = p
return np.array([2*x + 1.5*y, 1.5*x + 4*y])
def hessian(p):
# 二阶导全是常数
return np.array([[2, 1.5],
[1.5, 4]])
# --- 2. 选手一: Steepest Descent (小步慢跑) ---
def steepest_descent(start, lr=0.15, steps=20):
path = [start]
x = np.array(start)
for _ in range(steps):
grad = gradient(x)
x = x - lr * grad
path.append(x)
return np.array(path)
# --- 3. 选手二: Coordinate Descent (走楼梯) ---
def coordinate_descent(start, steps=10):
path = [start]
x, y = start
for _ in range(steps):
# 优化 x: d/dx = 2x + 1.5y = 0 -> x = -0.75y
x = -0.75 * y
path.append([x, y])
# 优化 y: d/dy = 1.5x + 4y = 0 -> y = -0.375x
y = -0.375 * x
path.append([x, y])
return np.array(path)
# --- 4. 选手三: Newton's Method (瞬间移动) ---
def newton_method(start, steps=5):
path = [start]
x = np.array(start)
H = hessian(x)
H_inv = np.linalg.inv(H) # 这里直接求逆,因为是常数矩阵
for _ in range(steps):
grad = gradient(x)
# 核心: x = x - H^-1 * g
x = x - H_inv @ grad
path.append(x)
# 对于二次函数,理论上一步就到了,但为了画图我们多跑几次(虽然都在原地)
if np.linalg.norm(grad) < 1e-6: break
return np.array(path)
# --- 5. 比赛开始 & 可视化 ---
start_pos = [8.0, -6.0] # 从远处出发
path_sd = steepest_descent(start_pos)
path_cd = coordinate_descent(start_pos)
path_newton = newton_method(start_pos)
# 作图
x_grid = np.linspace(-9, 9, 100)
y_grid = np.linspace(-9, 9, 100)
X, Y = np.meshgrid(x_grid, y_grid)
Z = X**2 + 1.5*X*Y + 2*Y**2
plt.figure(figsize=(10, 9))
plt.contour(X, Y, Z, levels=30, cmap='gray_r', alpha=0.3)
# 绘制路径
plt.plot(path_sd[:,0], path_sd[:,1], 'o-', color='red', label='Steepest Descent (Gradient)')
plt.plot(path_cd[:,0], path_cd[:,1], '.-', color='orange', label='Coordinate Descent (Staircase)')
plt.plot(path_newton[:,0], path_newton[:,1], 'x--', color='blue', lw=2, markersize=12, label="Newton's Method (Direct)")
# 标记起点终点
plt.scatter(start_pos[0], start_pos[1], color='black', s=100, label='Start')
plt.scatter(0, 0, marker='*', s=300, color='gold', zorder=10, label='Global Min')
plt.title("Deterministic Optimization Showdown\n$f(x,y) = x^2 + 1.5xy + 2y^2$")
plt.legend()
plt.axis('equal')
plt.grid(True, linestyle='--')
plt.show()
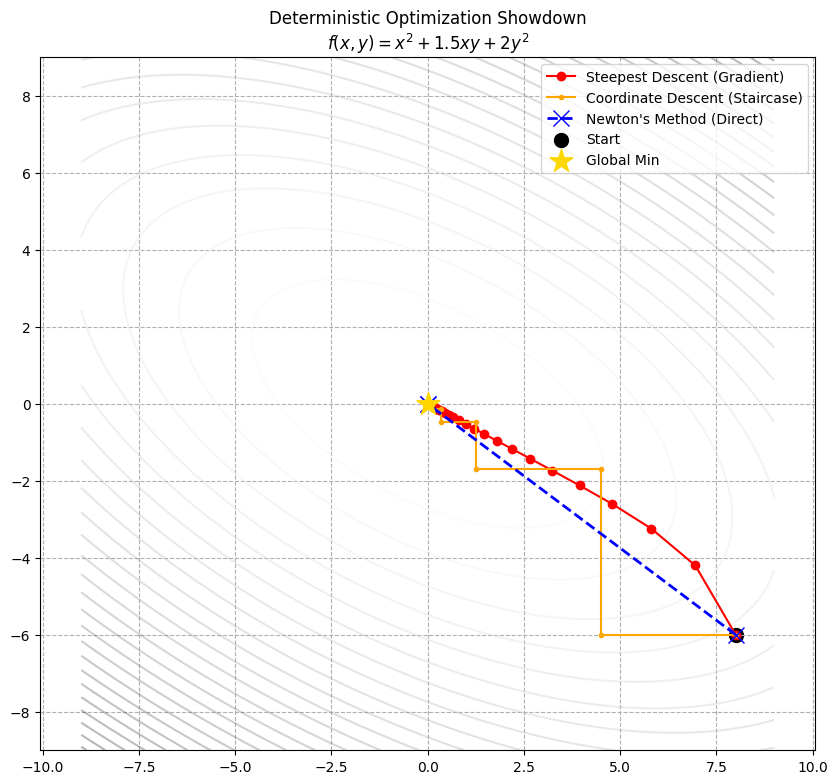
上面一张极其清晰的对比图:
- Newton’s Method (蓝线):
- 表现:直接画了一条直线,一步命中红心(金色的星星)。
- 原因:它拥有“上帝视角”(曲率信息)。它看穿了这个函数是个二次碗,计算出了精确的底坐标。
- 代价:入场费最贵(要算矩阵逆)。
- Steepest Descent (红线):
- 表现:走了一条平滑的曲线,虽然有点绕弯(因为它垂直于等高线走),但方向感还不错,稳步逼近中心。
- 原因:它只看局部斜率。虽然不如牛顿法直,但比只能走直角的坐标下降法灵活。
- 代价:性价比高,中规中矩。
- Coordinate Descent (橙线):
- 表现:经典的楼梯形状。
- 原因:由于 $1.5xy$ 这一项的存在,变量 $x$ 和 $y$ 是耦合的。
- 当你想优化 $x$ 时,不得不考虑 $y$;
- 当你动了 $x$ 后,$y$ 的最佳位置又变了。
- 这导致它只能在这两个变量之间来回拉扯,效率最低。
Scan to Share
微信扫一扫分享