这里以图像分割为例
贝叶斯图像分割的基石——似然与先验的博弈
在计算机视觉中,图像分割 (Image Segmentation) 的目标是给图片中的每一个像素打上标签(例如:属于前景还是背景) 。这里,我们将观测到的图像记为 $Y$ ($y_{ij} \in \mathbb{R}$),将要找的标签(Mask)记为 $L$ ($l_{ij} \in \{1, 2\}$)。
如果用贝叶斯的视角来看待这个问题,我们要寻找的是 后验概率 (Posterior),即在已知观测图像 $Y$ 的情况下,真实标签为 $L$ 的概率。
根据贝叶斯定理,后验概率 (Posterior) 可以写成:
$$p(x|y) = \frac{L(y|x)p(x)}{const}$$换成我们这里的变量就是:
$$p(L|Y) \propto P(Y|L) \cdot P(L)$$这个公式把一个极其困难的问题,拆成了两个可以分别解决的部分:
- 似然 (Likelihood) $P(Y|L)$:如果真实的标签真的是 $L$,那么生成眼前这幅含噪图像 $Y$ 的概率有多大 ?
- 先验 (Prior) $P(L)$:在我们还没看到图像之前,凭常识认为标签 $L$ 应该长什么样?
我们的终极目标是找到一个 $L$ ,使得似然和先验的乘积最大化,这就是所谓的 MAP (Maximum A Posteriori, 最大后验估计) 。
Python 示例:构建我们的“测试场”
在探讨如何求解之前,我们必须先用代码把这个“观测数据 ”和“真实标签 ”给造出来。
假设训练样本满足高斯分布:$y_{ij} | l_{ij}=1 \sim N[\mu_1, \sigma_1^2]$ 和 $y_{ij} | l_{ij}=2 \sim N[\mu_2, \sigma_2^2]$
下面这段代码将生成我们的 Ground Truth (真实标签) 以及带有高斯噪声的观测图像。
import numpy as np
import matplotlib.pyplot as plt
# ==========================================
# 1. 模拟真实世界 (Ground Truth)
# ==========================================
# 假设一张 50x50 的图像
rows, cols = 50, 50
true_L = np.ones((rows, cols)) # 背景标签为 1
# 画一个内部的正方形作为前景 (标签为 2)
true_L[15:35, 15:35] = 2
# ==========================================
# 2. 模拟观测过程 (Likelihood Generation)
# ==========================================
# 我们从训练样本中得知了不同标签的颜色分布参数 (均值 mu 和方差 sigma)
# 背景 (标签1) 偏暗,前景 (标签2) 偏亮
mu_1, sigma_1 = 0.0, 1.0
mu_2, sigma_2 = 3.0, 1.0
# 根据真实标签,加入高斯噪声生成观测图像 Y
Y = np.zeros_like(true_L, dtype=float)
# 给标签为 1 的像素赋予 N(mu_1, sigma_1) 的颜色值
Y[true_L == 1] = np.random.normal(mu_1, sigma_1, np.sum(true_L == 1))
# 给标签为 2 的像素赋予 N(mu_2, sigma_2) 的颜色值
Y[true_L == 2] = np.random.normal(mu_2, sigma_2, np.sum(true_L == 2))
# ==========================================
# 3. 可视化我们生成的数据
# ==========================================
fig, axes = plt.subplots(1, 2, figsize=(10, 5))
axes[0].imshow(true_L, cmap='gray')
axes[0].set_title("Ground Truth Mask (L)\nLabel 1(Black), Label 2(White)")
axes[0].axis('off')
axes[1].imshow(Y, cmap='viridis')
axes[1].set_title("Noisy Observation (Y)\nWhat the computer sees")
axes[1].axis('off')
plt.tight_layout()
plt.show()
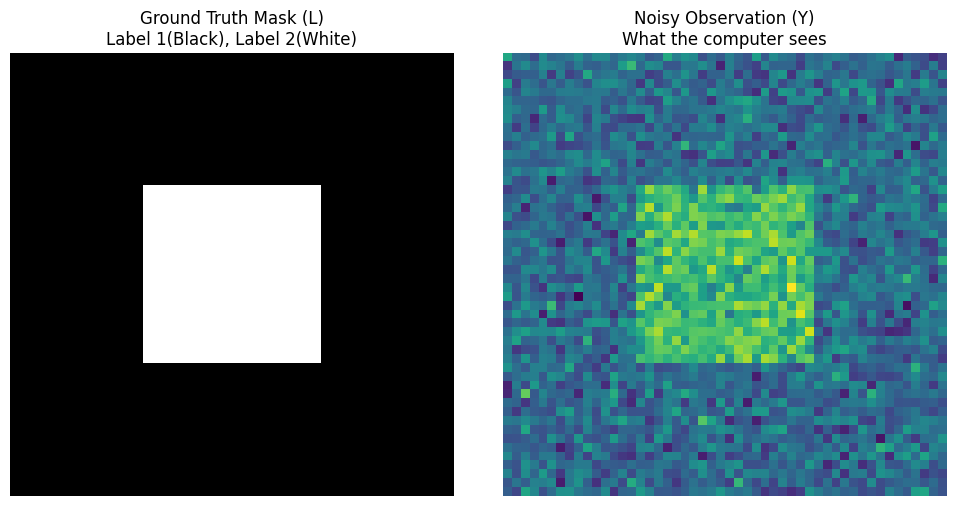
你会看到左边是完美的黑白正方形(上帝视角 $L$),而右边是布满噪点的彩色图像(凡人视角 $Y$)。 现在的任务是:计算机只拥有右图 $Y$ 和高斯参数,它该如何逆向推导出左图 $L$ 呢?
传统分类法——假设“绝对独立”带来的灾难
在真正引入贝叶斯 MRF 之前,我们有必要先看看“前人”是怎么做的,以及他们为什么失败了。这能让我们更深刻地体会到 MRF 的伟大。
传统方法 (Traditional Method) 进行了一个在图像处理中非常致命的假设:绝对独立 (Assume they’re independent)。
它假设每一个像素的标签 $l_i$ 都是自己管自己的,和它旁边的像素毫无关系:
$$P(\underline{L}) = \prod_i P(l_i)$$“各人自扫门前雪”的分类逻辑
因为假设了像素之间绝对独立,先验概率 $P(L)$ 就变成了一个常数或者完全不起作用。计算机在分类时,只会盯着当前这一个像素的颜色看 (The classification only considers itself)。
它的逻辑非常简单粗暴:
- 看看当前像素的值 $y_{ij}$。
- 算一下它属于标签 1(背景)的高斯概率 $P(y_{ij}|l_{ij}=1)$。
- 算一下它属于标签 2(前景)的高斯概率 $P(y_{ij}|l_{ij}=2)$。
- 谁的概率大,就把它归为哪一类。(这就是纯粹的极大似然估计 MLE)
Python 示例:实现传统分类并见证“灾难”
我们承接上一节生成的观测数据 Y,用几行代码来实现这个传统方法。
# ==========================================
# 承接上一节的变量: Y, mu_1, sigma_1, mu_2, sigma_2
# ==========================================
# 我们要找的传统方法分类结果 L_traditional
L_traditional = np.ones_like(Y)
# 1. 计算每个像素属于标签 1 (背景) 的似然概率
# 依据正态分布公式 N(mu_1, sigma_1^2)
likelihood_1 = np.exp(-0.5 * ((Y - mu_1) / sigma_1)**2) / sigma_1
# 2. 计算每个像素属于标签 2 (前景) 的似然概率
# 依据正态分布公式 N(mu_2, sigma_2^2)
likelihood_2 = np.exp(-0.5 * ((Y - mu_2) / sigma_2)**2) / sigma_2
# 3. 简单粗暴的比较:如果属于前景的概率更大,就把标签设为 2
L_traditional[likelihood_2 > likelihood_1] = 2
# ==========================================
# 可视化传统方法的灾难结果
# ==========================================
fig, axes = plt.subplots(1, 3, figsize=(12, 4))
axes[0].imshow(true_L, cmap='gray')
axes[0].set_title("Ground Truth")
axes[0].axis('off')
axes[1].imshow(Y, cmap='viridis')
axes[1].set_title("Noisy Observation (Y)")
axes[1].axis('off')
axes[2].imshow(L_traditional, cmap='gray')
axes[2].set_title("Traditional Method\n(Noisy & Isolated pixels)")
axes[2].axis('off')
plt.tight_layout()
plt.show()
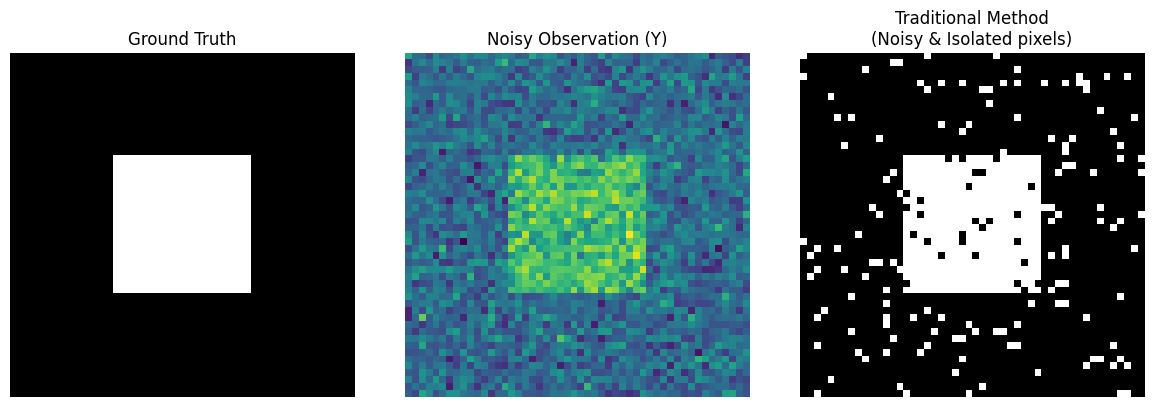
注意上面的第三张图(Traditional Method):它虽然勉强凑出了一个正方形的轮廓,但正方形里面全是黑色的“麻子”,外面的背景里也全是白色的“雪花” 。
为什么会这样呢?
因为高斯噪声会让某些背景像素的值突然变得很高,传统方法“只见树木不见森林”,一看数值高,立马把它错认为前景。它完全没有 “物理世界是连续的,一个白点周围如果全是黑点,那它大概率是个噪点” 这种常识。
贝叶斯 MRF 方法——引入“空间常识” (Modeling the Homogeneity)
上面的运行结果告诉我们,做图像分割绝对不能“只看自己”。真实的物理世界是连续的:一个像素如果是前景,那它周围的像素大概率也是前景。
因此,我们 “不再假设绝对独立 (Not Assume independency anymore)”!我们要用贝叶斯方法结合 MRF,把“空间常识”教给计算机。
似然函数:依然各司其职
在贝叶斯公式 $P(L|Y) \propto P(Y|L) P(L)$ 中,对于前半部分的似然函数 $P(Y|L)$,我们仍然保持独立假设:生成图像颜色的过程,是各个像素在高斯分布下独立生成的。
$$L(\underline{Y}|\underline{L}) = \prod_i P(y_i|l_i)$$先验概率的进化:同质性建模 (Modeling the Homogeneity)
魔法发生在后半部分的先验概率 $P(L)$ 上。既然像素标签不再独立,我们要如何用数学描述“它们靠得很近”?
一个绝佳的方案:把它定义为一个 Gibbs 分布!
$$p(\underline{l}) = A e^{-E(\underline{l})}$$这里的核心是吉布斯能量 (Gibbs Energy) $E(L)$。我们要设计一个惩罚机制:
- 如果我和我的邻居标签一样(同质),能量就很低,系统很开心。
- 如果我和我的邻居标签不一样(差异),系统就会施加一个 “差异惩罚 (penalty for diff)”。
利用邻居定义的“团 (Clique)”,我们可以写出这个惩罚公式:
$$U_c(l_c) = \alpha |l_i - l_j|$$这里的 $\alpha$ 是一个极其关键的超参数,它代表了 “你有多希望图像保持平滑 (how strong you want the homogeneity)”。$\alpha$ 越大,计算机就越不敢随便把一个像素标记为和周围不同的异类。
后验概率的最终形态
现在,把似然和先验乘起来,我们就得到了下面这个终极公式:
$$Pr(\underline{L}|\underline{Y}) \propto \prod_i \frac{1}{\sqrt{2\pi\sigma(l_i)^2}} e^{-\frac{1}{2\sigma(l_i)^2}(y_i - \mu(l_i))^2} \cdot e^{-\sum_c \alpha|l_i - l_j|}$$这个公式看着很长,但如果你对它取负对数 (-log),它就会变成一个非常优雅的“能量最小化”问题。
对于任意一个像素 $i$,它取某个标签 $l_i$ 的总能量等于:
总能量 = 数据项 (似然) + 平滑项 (先验)
Python 示例:用代码写出“总能量”探测器
为了给下一节的优化做准备,我们要先把这个“算能量”的函数写出来。这可是 MRF 的灵魂探测器。
# ==========================================
# 承接之前的变量:
# Y (观测图像)
# mu_1, sigma_1 (标签 1 背景的高斯参数)
# mu_2, sigma_2 (标签 2 前景的高斯参数)
# ==========================================
def get_pixel_energy(padded_L, Y, r, c, label_candidate, alpha):
"""
计算点 (r, c) 假设取值为 label_candidate 时的总吉布斯能量
padded_L: 当前打好 padding 的标签图 (为了方便找邻居)
"""
# 1. 数据项 (Data Term, 源自似然函数)
# 取负对数后: (y - mu)^2 / (2*sigma^2) + log(sigma)
y_val = Y[r-1, c-1]
if label_candidate == 1:
energy_data = 0.5 * ((y_val - mu_1) / sigma_1)**2 + np.log(sigma_1)
else:
energy_data = 0.5 * ((y_val - mu_2) / sigma_2)**2 + np.log(sigma_2)
# 2. 平滑项 (Smoothness Term, 源自先验 MRF)
# 对应公式: alpha * sum(|l_i - l_j|)
# 找出上下左右四个邻居
neighbors = [padded_L[r-1, c], padded_L[r+1, c],
padded_L[r, c-1], padded_L[r, c+1]]
# 计算当前候选标签与邻居标签的差异惩罚
energy_smooth = alpha * sum([abs(label_candidate - n) for n in neighbors])
# 3. 返回总能量 (能量越低,说明这个候选标签越靠谱)
return energy_data + energy_smooth
# 我们来随便测试一个点
# 假设用传统方法得到的 L_traditional 给它加上 padding
padded_L_test = np.pad(L_traditional, 1, mode='edge')
# 测试坐标 (25, 25) 属于标签 1 和标签 2 的能量 (假设 alpha=1.2)
e1 = get_pixel_energy(padded_L_test, Y, 25, 25, label_candidate=1, alpha=1.2)
e2 = get_pixel_energy(padded_L_test, Y, 25, 25, label_candidate=2, alpha=1.2)
print(f"坐标(25, 25) 变为背景(1)的能量: {e1:.2f}")
print(f"坐标(25, 25) 变为前景(2)的能量: {e2:.2f}")
print("结论:系统会更倾向于能量较低的那个标签!")
坐标(25, 25) 变为背景(1)的能量: 7.23
坐标(25, 25) 变为前景(2)的能量: 1.25
结论:系统会更倾向于能量较低的那个标签!
寻找 MAP 的终极武器——模拟退火与 Gibbs 采样
在上一节,我们成功写出了“总能量”的计算公式。系统总能量越低,代表后验概率越大,这个图像分割的结果就越完美。
但是,面对一张 的图像,哪怕每个像素只有两个标签(1 或 2),总共也有 $2^{2500}$ 种可能的组合!我们不可能穷举所有的标签组合去寻找能量最低的那一个。
那么,要如何在这个天文数字级别的解空间里找到最优解呢?
模拟退火 (Simulated Annealing, SA) 配合 Gibbs 采样器 (Gibbs Sampler)。
内层引擎:Gibbs 采样器 (Gibbs Sampler)
如果我们想同时更新所有像素,系统会直接崩溃。Gibbs 采样的核心智慧是:每次只盯着一个像素看,假装其他所有像素都是固定不动的。
而且得益于 MRF 的马尔可夫性,在更新当前像素时,我们 “只看邻居” (only neighbors)。
- 算一下当前像素变成标签 1 的能量 $E_1$。
- 算一下当前像素变成标签 2 的能量 $E_2$。
- 利用吉布斯公式把能量转化为概率,然后掷骰子决定它最终变成谁。
外层指挥官:模拟退火 (Simulated Annealing)
为了防止 Gibbs 采样陷入局部死胡同(比如被一块顽固的噪点卡住),我们需要引入“温度 $T$”。 “SA 需要通过 Gibbs 采样来进行采样 (the S.A. requires a sampling done by a Gibbs Sample)”。
- 高温期:系统非常活跃,即使某个标签会让能量变高(变差),也有一定概率被接受。这让算法有能力跳出“麻子”陷阱。
- 降温期:随着迭代进行,系统逐渐“冷却”,越来越趋向于只接受能让能量降低(变好)的标签。最终冻结在完美的 MAP(最大后验估计)状态。
Python 示例:见证奇迹的时刻!
现在,我们要把前面所有的代码积木拼装在一起。我们要初始化一个起点 $L_0$ (Init $L_0$),然后启动这台强大的贝叶斯 MRF 引擎!
# ==========================================
# 承接之前的变量:
# true_L (完美标签), Y (含噪图像), L_traditional (传统方法结果)
# get_pixel_energy() 函数
# ==========================================
def mrf_bayesian_segmentation(Y, initial_L, alpha=1.2, iter_max=15, T_init=3.0, T_end=0.1):
"""
使用 模拟退火 + Gibbs 采样 寻找图像分割的最大后验估计 (MAP)
"""
rows, cols = Y.shape
# 1. 初始化起点 (Init L0)
# 为了加快收敛,我们直接拿传统方法的结果作为起点,而不是瞎猜
L = np.copy(initial_L)
# 计算几何降温系数
tau = -np.log(T_end / T_init) / (iter_max - 1)
print("🚀 开始启动贝叶斯 MRF 优化引擎...")
# 外层循环:模拟退火 (SA)
for it in range(iter_max):
T = T_init * np.exp(-tau * it) # 当前温度
# 给图像加一圈 Padding,方便处理边界像素的邻居
padded_L = np.pad(L, 1, mode='edge')
# 内层循环:Gibbs Sampler 扫描全图
for r in range(1, rows + 1):
for c in range(1, cols + 1):
# 计算取标签 1 和标签 2 时的局部总能量
E_1 = get_pixel_energy(padded_L, Y, r, c, label_candidate=1, alpha=alpha)
E_2 = get_pixel_energy(padded_L, Y, r, c, label_candidate=2, alpha=alpha)
# 利用吉布斯公式,将能量差转化为概率
# P(L=1) = exp(-E_1/T) / (exp(-E_1/T) + exp(-E_2/T))
# 为防止指数溢出,化简为 Logistic 形式:
prob_1 = 1.0 / (1.0 + np.exp((E_1 - E_2) / T))
# 掷骰子!(根据概率进行采样)
if np.random.rand() < prob_1:
padded_L[r, c] = 1
else:
padded_L[r, c] = 2
# 剥去 padding,更新整张图的标签
L = padded_L[1:-1, 1:-1]
print(f"迭代 {it+1}/{iter_max} 完成 | 当前温度 T = {T:.2f}")
return L
# 运行 MRF 分割算法 (惩罚系数 alpha 设为 1.2)
L_mrf = mrf_bayesian_segmentation(Y, initial_L=L_traditional, alpha=1.2)
# ==========================================
# 终极可视化大比拼
# ==========================================
fig, axes = plt.subplots(1, 4, figsize=(16, 4))
axes[0].imshow(true_L, cmap='gray')
axes[0].set_title("1. Ground Truth (God's perspective)")
axes[0].axis('off')
axes[1].imshow(Y, cmap='viridis')
axes[1].set_title("2. Noisy Y (From a mortal's perspective)")
axes[1].axis('off')
axes[2].imshow(L_traditional, cmap='gray')
axes[2].set_title("3. Traditional (I don't care my neighbors)")
axes[2].axis('off')
axes[3].imshow(L_mrf, cmap='gray')
axes[3].set_title("4. Bayesian MRF (Modeling the Homogeneity)")
axes[3].axis('off')
plt.tight_layout()
plt.show()
🚀 开始启动贝叶斯 MRF 优化引擎...
迭代 1/15 完成 | 当前温度 T = 3.00
迭代 2/15 完成 | 当前温度 T = 2.35
迭代 3/15 完成 | 当前温度 T = 1.85
迭代 4/15 完成 | 当前温度 T = 1.45
迭代 5/15 完成 | 当前温度 T = 1.14
迭代 6/15 完成 | 当前温度 T = 0.89
迭代 7/15 完成 | 当前温度 T = 0.70
迭代 8/15 完成 | 当前温度 T = 0.55
迭代 9/15 完成 | 当前温度 T = 0.43
迭代 10/15 完成 | 当前温度 T = 0.34
迭代 11/15 完成 | 当前温度 T = 0.26
迭代 12/15 完成 | 当前温度 T = 0.21
迭代 13/15 完成 | 当前温度 T = 0.16
迭代 14/15 完成 | 当前温度 T = 0.13
迭代 15/15 完成 | 当前温度 T = 0.10
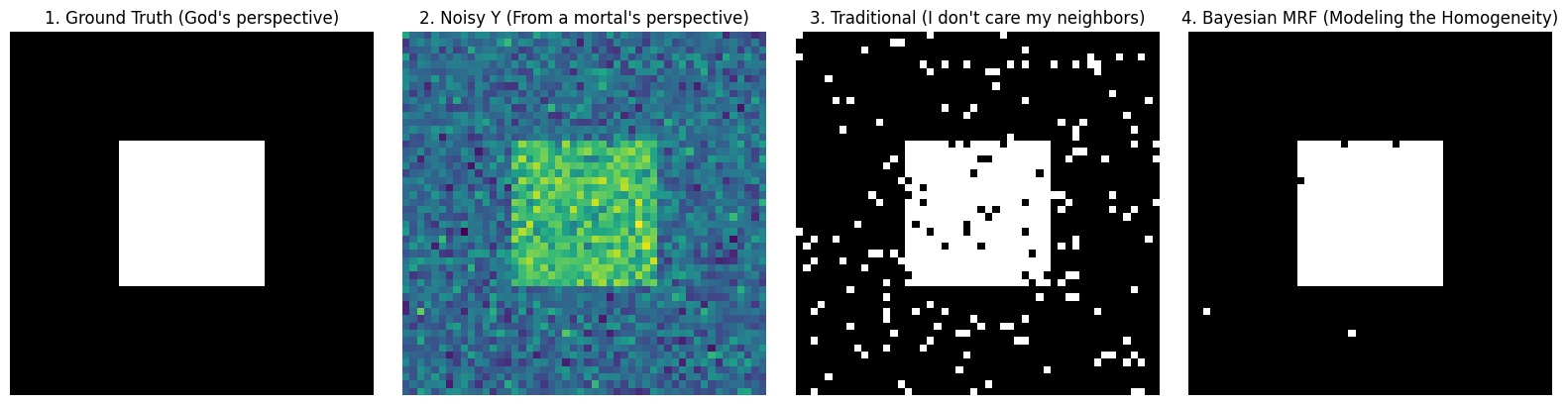
仔细看看上面的图:
- 图 3(传统方法):因为它假设像素绝对独立,所以被高斯噪声彻底欺骗了,画面里全是误分类的“雪花点”。
- 图 4(贝叶斯 MRF):奇迹发生了!在惩罚系数 施加的“同质性先验”和模拟退火算法的步步逼近下,系统硬生生把那些孤立的噪点一个个“洗掉”了。它不仅完美恢复了正方形的清晰边界,甚至找回了那份干净、平滑的视觉美感。
这,就是贝叶斯统计与马尔可夫随机场(MRF)交织出的巅峰之作!
终极实战——从“黑猫”图像分割看透贝叶斯 MRF
在前几节中,我们推导了高深的公式,并用极简的代码演示了原理。现在,是时候打真正的硬仗了。
这个实战的目标是从一张充满噪点的图片中,把一只“黑猫”(前景,标签设为 1)从背景(标签设为 2)中抠出来。
在真实的图像中,背景和前景的颜色并不是非黑即白的,它们服从高斯分布。我们根据训练样本(训练数据)来计算每个类别的均值和标准差
- 黑猫的颜色均值较暗 $\mu_1 = 19$,方差 $\sigma_1 = 23$;
- 而背景较亮 $\mu_2 = 209$,方差 $\sigma_2 = 29$。
我们尝试图像分割的三种方法:
方法一:朴素的极大似然估计 (Maximum Likelihood)
这是最简单的做法。它完全忽略了像素间的空间关系。对于每一个像素,它只计算:如果这个像素属于黑猫,高斯概率是多少?属于背景,高斯概率又是多少?谁大选谁。
- 预期结果:图像中会充满星星点点的“雪花”噪点。
方法二:MRF + 模拟退火 + Gibbs 采样 (Stochastic)
它把像素的局部马尔可夫性(MRF)考虑了进去。根据代码中的公式,像素 $x_i$ 的条件概率 $p_T(x_i | x_{-i}, y)$ 被转换为一个极其优雅的能量函数:
$$E(x_i) = \log(\sigma_{x_i}) + \frac{(y_i - \mu_{x_i})^2}{2\sigma_{x_i}^2} + \alpha \sum_{j \in \text{neighbors}} |x_i - x_j|$$- 第一项和第二项:是数据项 (Likelihood),惩罚不符合高斯分布的颜色。
- 第三项:是平滑项 (Prior),通过惩罚系数 $\alpha$ (代码中设为惊人的 30),强烈要求当前像素必须和周围邻居保持一致。
然后,利用模拟退火从高温降到低温,配合 Gibbs 采样掷骰子,最终求得完美解。
方法三:简单松弛法 (Simple Relaxation / ICM)
模拟退火虽然好,但由于要掷骰子(随机采样),速度比较慢。
因此,工业界常用的妥协方案之一是:简单松弛法 (Simple Relaxation)(在学术界通常被称为 ICM, Iterated Conditional Modes)。 它的计算公式和方法二完全一样,但它不掷骰子!在更新每个像素时,它直接贪婪地选择那个让能量最低(概率最大)的标签。迭代几次后,一旦图像不再变化,立刻停止。
Python 实战:三大方法代码大比拼
下面代码中,先自动生成一只带有高斯噪声的“合成黑猫”,然后分别用这三种方法对它进行分割。
⚠️ 代码核心看点:
注意看 MRF_Gibbs_SA 函数中的对数-指数求和技巧 (Log-Sum-Exp Trick)。当能量值很高时,直接算 $e^{-\text{Energy}}$ 会导致计算机数值下溢(变成 0)。我们减去了最大值 lnA = -max(...) 来进行数值正则化。这是非常宝贵的工程经验!
import numpy as np
import matplotlib.pyplot as plt
# ==========================================
# 0. 数据准备:生成“合成黑猫”带噪图像
# ==========================================
rows, cols = 80, 80
true_L = np.ones((rows, cols), dtype=int) * 2 # 背景标签设为 2
# 画一只“抽象的黑猫”在中间 (标签设为 1)
true_L[20:60, 30:50] = 1
true_L[15:20, 30:35] = 1 # 左耳
true_L[15:20, 45:50] = 1 # 右耳
# 真实的高斯分布参数 (参照 MATLAB 设定)
mu_x = {1: 100.0, 2: 180.0} # 1:黑猫(暗), 2:背景(亮)
sigma_x = {1: 30.0, 2: 30.0}
# 加上高斯噪声生成观测图像 Y
Y = np.zeros_like(true_L, dtype=float)
for r in range(rows):
for c in range(cols):
label = true_L[r, c]
Y[r, c] = np.random.normal(mu_x[label], sigma_x[label])
# 限制像素值在 0~255
Y = np.clip(Y, 0, 255)
# ==========================================
# 境界一:朴素极大似然估计 (No MRF)
# ==========================================
def maximum_likelihood(Y):
L_ml = np.zeros_like(Y, dtype=int)
# 对于每个点,算算属于 1 和 2 的似然能量 (只看数据项)
for r in range(rows):
for c in range(cols):
# 能量 = log(sigma) + (y - mu)^2 / (2*sigma^2)
E1 = np.log(sigma_x[1]) + (Y[r, c] - mu_x[1])**2 / (2 * sigma_x[1]**2)
E2 = np.log(sigma_x[2]) + (Y[r, c] - mu_x[2])**2 / (2 * sigma_x[2]**2)
L_ml[r, c] = 1 if E1 < E2 else 2 # 谁能量低(概率大)选谁
return L_ml
# ==========================================
# 境界二:MRF + 模拟退火 + Gibbs 采样
# ==========================================
def mrf_simulated_annealing(Y, initial_L, alpha=30, iter_max=50, Tin=100, Tend=0.01):
L = np.copy(initial_L)
tau = -np.log(Tend / Tin) / (iter_max - 1)
for it in range(iter_max):
T = Tin * np.exp(-tau * it)
padded_L = np.pad(L, 1, mode='edge')
for r in range(1, rows + 1):
for c in range(1, cols + 1):
neighbors = [padded_L[r-1, c], padded_L[r+1, c], padded_L[r, c-1], padded_L[r, c+1]]
pt_xi = {}
for k in [1, 2]:
# 总能量 = 数据项 + 平滑项 (alpha * 差异)
E_data = np.log(sigma_x[k]) + (Y[r-1, c-1] - mu_x[k])**2 / (2 * sigma_x[k]**2)
E_smooth = alpha * sum([abs(k - n) for n in neighbors])
# Gibbs 概率指数部分
pt_xi[k] = - (1.0 / T) * (E_data + E_smooth)
# [工程技巧] 数值正则化:防止指数溢出
max_pt = max(pt_xi[1], pt_xi[2])
p1 = np.exp(pt_xi[1] - max_pt)
p2 = np.exp(pt_xi[2] - max_pt)
# 归一化转为概率并掷骰子
prob_1 = p1 / (p1 + p2)
padded_L[r, c] = 1 if np.random.rand() < prob_1 else 2
L = padded_L[1:-1, 1:-1]
return L
# ==========================================
# 境界三:简单松弛法 (Simple Relaxation)
# ==========================================
def simple_relaxation(Y, initial_L, alpha=30, iter_max=50):
L = np.copy(initial_L)
for it in range(iter_max):
L_prec = np.copy(L)
padded_L = np.pad(L, 1, mode='edge')
for r in range(1, rows + 1):
for c in range(1, cols + 1):
neighbors = [padded_L[r-1, c], padded_L[r+1, c], padded_L[r, c-1], padded_L[r, c+1]]
E = {}
for k in [1, 2]:
E_data = np.log(sigma_x[k]) + (Y[r-1, c-1] - mu_x[k])**2 / (2 * sigma_x[k]**2)
E_smooth = alpha * sum([abs(k - n) for n in neighbors])
# 松弛法不需要除以温度 T
E[k] = E_data + E_smooth
# [核心差异] 不掷骰子,直接贪心选择能量最低的标签
padded_L[r, c] = 1 if E[1] < E[2] else 2
L = padded_L[1:-1, 1:-1]
# 提前停止机制:如果图像不再发生变化,说明收敛了
if np.sum(np.abs(L_prec - L)) == 0:
print(f"简单松弛法在第 {it+1} 次迭代时提前收敛!")
break
return L
# 运行对比实验
print("1. 正在计算极大似然估计...")
L_ml = maximum_likelihood(Y)
print("2. 正在运行 MRF 模拟退火...")
L_sa = mrf_simulated_annealing(Y, initial_L=L_ml, alpha=1.5)
print("3. 正在运行 MRF 简单松弛法...")
L_sr = simple_relaxation(Y, initial_L=L_ml, alpha=1.5)
# 可视化结果
fig, axes = plt.subplots(1, 5, figsize=(18, 4))
titles = ["1. Ground Truth", "2. Noisy Y", "3. Maximum Likelihood", "4. MRF + SA (Stochastic)", "5. MRF + SR (Deterministic)"]
images = [true_L, Y, L_ml, L_sa, L_sr]
for ax, img, title in zip(axes, images, titles):
ax.imshow(img, cmap='gray' if title != "2. Noisy Y" else 'viridis')
ax.set_title(title)
ax.axis('off')
plt.tight_layout()
plt.show()
1. 正在计算极大似然估计...
2. 正在运行 MRF 模拟退火...
3. 正在运行 MRF 简单松弛法...
简单松弛法在第 3 次迭代时提前收敛!
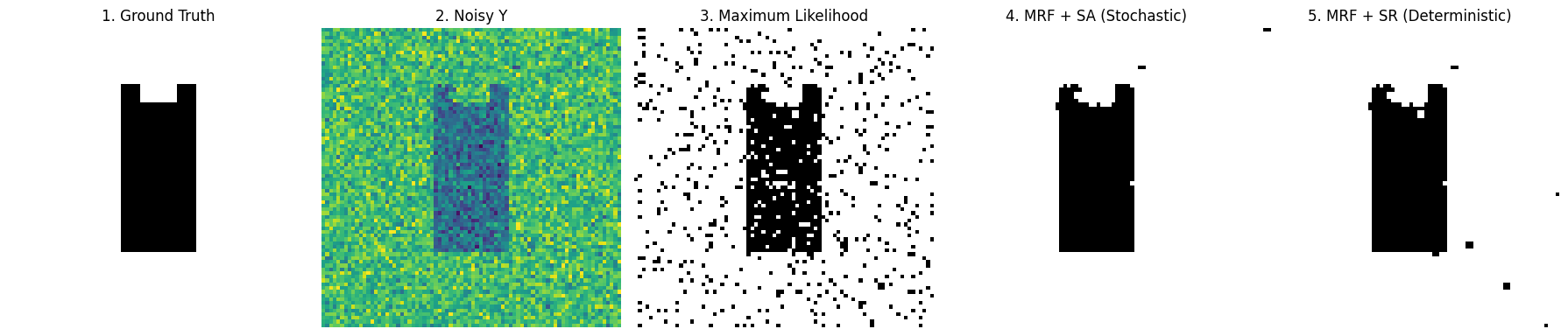
看看上面 5 张对比图
- 图 3 (极大似然):像一张劣质的黑白报纸,全是白色的噪点。这就是抛弃空间先验的代价。
- 图 4 (模拟退火 SA):完美还原了黑猫的形状。因为它经过了高温的洗礼,成功跳出了局部最优的陷阱。
- 图 5 (简单松弛 SR):速度极快,也能还原轮廓。但由于它太贪心(不接受变差的结果),图像边缘往往不如 SA 那样平滑,偶尔会卡在死胡同里出不来。
终极彩蛋:工业界的黄金搭档——“随机粗调”与“确定性精调”
在跑完上面的代码后,你可能会有一个疑问:既然模拟退火 (SA) 那么厉害,为什么我们还需要 ICM(简单松弛法)?
这就触及到了算法工程界的一个核心痛点:Stochastic(随机算法)通常只能得到“近似最优解”,而无法做到“绝对最优”。
为什么 SA 只能“近似”?
- 模拟退火在理论上确实能找到全局最优,但前提是“时间无限长,降温无限慢”。
- 在实际写代码时,为了让程序在几秒钟内跑完,我们的降温步数(
iter_max)通常是有限的,降温系数也是妥协过的。这就导致在迭代的最后,温度 $T$ 并没有真正降到绝对的 0。 - 只要 $T > 0$,Gibbs 采样就永远存在“掷骰子”的随机性。它可能会在全局最优解的附近反复横跳(Jittering),给你一个 $99\%$ 接近完美的解,但就是没法彻底锁死在那个绝对的最底端。
为什么 ICM 是“危险的快刀”?
- ICM(简单松弛法)是确定性的 (Deterministic)。它不掷骰子,极其贪婪:只要能让能量下降,它就毫不犹豫地走过去;一旦无路可走,它就立刻停下。
- 它的优点是收敛极快,且能达到绝对的局部最优;缺点是视野极窄,如果初始点选得不好,它会瞬间掉进错误的“局部死胡同”里出不来。
终极奥义:混合双打 (Stochastic + Deterministic)
既然它们各有优缺点,为什么不把它们结合起来呢?这就诞生了 MRF 优化的终极范式:先用 SA 粗调,再用 ICM 精调。
这就好比打高尔夫球:
- 第一杆(模拟退火 SA):大力出奇迹。利用它的随机性和跳跃能力,跨越各种局部陷阱,把球打到离洞口非常近的果岭上(找到近似最优解)。
- 第二杆(简单松弛 ICM):精准推杆。把 SA 得到的近似解作为起点,利用它贪婪、确定性的特点,一杆进洞,消除最后那一丁点随机噪点,稳稳落入能量最低点(锁定绝对最优解)。
Python 实战:完成这套“混合连招”
在代码实现上,这套连招极其简单,只需要把 SA 的输出结果,当作 ICM 的输入起点即可。
# ==========================================
# 终极连招:Hybrid Optimization (SA -> ICM)
# ==========================================
print("🚀 Step 1: 启动模拟退火 (SA) 进行全局粗调...")
# 稍微跑一跑 SA,不需要跑太多次,把大面积的噪点洗掉,找到大致的坑底
L_approx_opt = mrf_simulated_annealing(Y, initial_L=L_ml, alpha=5.0, iter_max=30)
print("🎯 Step 2: 启动简单松弛法 (ICM) 进行局部精调...")
# 把 SA 的结果 (L_approx_opt) 直接喂给 ICM 作为初始起点 (initial_L)
L_absolute_opt = simple_relaxation(Y, initial_L=L_approx_opt, alpha=5.0, iter_max=20)
print("✅ 优化完成!我们得到了绝对的最优分割 MAP。")
🚀 Step 1: 启动模拟退火 (SA) 进行全局粗调...
🎯 Step 2: 启动简单松弛法 (ICM) 进行局部精调...
简单松弛法在第 1 次迭代时提前收敛!
✅ 优化完成!我们得到了绝对的最优分割 MAP。
原理解析: 因为 SA 已经帮 ICM 排除了所有的“错误陷阱”,并把它送到了全局最优解的门口。此时启动 ICM,它那贪婪且确定性的下坡能力,会像重力一样,将图像中最后残余的几颗因 SA 随机性导致的“躁动像素”彻底压平,瞬间达成 $100\%$ 的收敛。
这,才是解决复杂非凸优化问题时,真正的大师级手法!
Scan to Share
微信扫一扫分享