import numpy as np
import matplotlib.pyplot as plt

def estimate_pi(N=1000):
    # 1. Sample N points in square [-1, 1] x [-1, 1]
    # np.random.rand generates [0, 1), so scaled to [-1, 1)
    x = np.random.uniform(-1, 1, N)
    y = np.random.uniform(-1, 1, N)
    
    # 2. Check how many fall inside unit circle
    r2 = x**2 + y**2
    inside = (r2 <= 1.0)
    k = np.sum(inside)
    
    # 3. Estimate pi
    pi_hat = 4.0 * k / N
    
    # 4. Standard Error & 95% Confidence Interval (Normal approx)
    # Variance of the Bernoulli indicator is p(1-p), where p = pi/4
    p_hat = k / N
    se_p = np.sqrt(p_hat * (1 - p_hat) / N)
    se_pi = 4.0 * se_p
    ci_lower = pi_hat - 1.96 * se_pi
    ci_upper = pi_hat + 1.96 * se_pi
    
    return pi_hat, (ci_lower, ci_upper), x, y, inside

# Run
np.random.seed(42)
N = 2000
pi_est, pi_ci, x, y, ins = estimate_pi(N)

print(f"Monte Carlo Estimation of π (N={N})")
print(f"Estimated π = {pi_est:.5f}")
print(f"95% CI = [{pi_ci[0]:.5f}, {pi_ci[1]:.5f}]")
print(f"True π = {np.pi:.5f}")

# Plot
plt.figure(figsize=(6,6))
plt.scatter(x[ins], y[ins], s=10, alpha=0.6, label='Inside')
plt.scatter(x[~ins], y[~ins], s=10, alpha=0.6, label='Outside')
plt.title(f"Monte Carlo Pi Estimation (N={N})\n$\\hat{{\\pi}} = {pi_est:.4f}$")
plt.xlabel("x")
plt.ylabel("y")
plt.legend(loc='upper right')
plt.axis('equal') # Keep aspect ratio circular
plt.show()

# Compute relative error for different N
Ns = np.logspace(2, 6, 20).astype(int) # N from 100 to 1,000,000
errors = []

true_pi = np.pi

# To smooth the curve, average over multiple runs for each N
trials = 50

for n_val in Ns:
    estimates = []
    for _ in range(trials):
        est, _, _, _, _ = estimate_pi(n_val)
        estimates.append(est)
    mean_est = np.mean(estimates)
    # Relative error of the mean estimate
    rel_err = np.abs(mean_est - true_pi) / true_pi
    errors.append(rel_err)

# Plot
plt.figure(figsize=(8,5))
plt.loglog(Ns, errors, 'o-', label='Simulation Error')
plt.loglog(Ns, 1.0/np.sqrt(Ns), 'k--', label='Theoretical Rate $O(1/\\sqrt{N})$')
plt.xlabel('Number of Samples N')
plt.ylabel('Relative Error |$\\hat{\\pi} - \\pi$| / $\\pi$')
plt.title('Monte Carlo Convergence Rate')
plt.legend()
plt.grid(True, which="both", ls="-")
plt.show()

from scipy.stats import beta, uniform

# Target: Beta(2, 5)
a, b = 2, 5
target_dist = beta(a, b)

# Proposal: Uniform(0, 1)
proposal_dist = uniform(0, 1)

# Find M: Max of p(x)/q(x)
x_vals = np.linspace(0.001, 0.999, 1000)
M = np.max(target_dist.pdf(x_vals) / proposal_dist.pdf(x_vals))
print(f"Optimal M = {M:.4f}")
# In practice, use slightly larger M to be safe (e.g., M=2.6) or exactly calculated max.

def rejection_sampling_beta(n_samples, M_val):
    samples = []
    attempts = 0
    while len(samples) < n_samples:
        attempts += 1
        x = np.random.uniform(0, 1) # Sample from q
        u = np.random.uniform(0, 1) # Decision variable
        
        # Accept condition
        ratio = target_dist.pdf(x) / (M_val * proposal_dist.pdf(x))
        if u <= ratio:
            samples.append(x)
            
    return np.array(samples), attempts

n_draws = 5000
samples, total_attempts = rejection_sampling_beta(n_draws, M_val=M)

print(f"Acceptance Rate: {n_draws / total_attempts:.2%}")
print(f"Theoretical Rate (1/M): {1/M:.2%}")

# Plot
plt.figure(figsize=(8,5))
# Histogram of samples
plt.hist(samples, bins=40, density=True, alpha=0.6, label='Rejection Samples')
# Theoretical Target PDF
plt.plot(x_vals, target_dist.pdf(x_vals), 'r-', lw=2, label='Target Beta(2,5)')
# M * q(x)
plt.plot(x_vals, M * proposal_dist.pdf(x_vals), 'k--', lw=2, label='Proposal M*q(x)')

plt.legend()
plt.title("Rejection Sampling: Beta(2,5) from Uniform")
plt.show()

# Rejection Sampling: Standard Normal (positive half) via Exponential(1)
# Target p(x) = (2/sqrt(2pi)) * exp(-x^2/2) for x>=0
# Proposal q(x) = exp(-x) for x>=0

def target_pdf(x):
    return (2.0 / np.sqrt(2 * np.pi)) * np.exp(-x**2 / 2)

def proposal_pdf(x):
    return np.exp(-x)

# Optimal M
M = 1.32  # calculated approx 1.315...

def rejection_normal_from_exp(n):
    res = []
    tot = 0
    while len(res) < n:
        tot += 1
        # Sample from Exp(1)
        x = np.random.exponential(scale=1.0)
        u = np.random.rand()
        
        acc_prob = target_pdf(x) / (M * proposal_pdf(x))
        if u <= acc_prob:
            res.append(x)
    return np.array(res), tot

s_norm, tot_N = rejection_normal_from_exp(2000)

print(f"Empirical Acceptance Rate: {2000/tot_N:.3%}")
print(f"Theoretical (1/M): {1/M:.3%}")

plt.figure(figsize=(8,5))
plt.hist(s_norm, bins=30, density=True, alpha=0.5, label='Samples')
xx = np.linspace(0, 4, 200)
plt.plot(xx, target_pdf(xx), 'r', label='Half-Normal PDF')
plt.plot(xx, M*proposal_pdf(xx), 'g--', label='Envelope M*Exp(1)')
plt.legend()
plt.title("Rejection Sampling: Half-Normal from Exp(1)")
plt.show()

# Code to re-illustrate the connection between Rejection Sampling and Pi estimation
# We count how many 'accepted' from Uniform Square
# p_hat = accepted / total ~ pi / 4

import scipy.stats as stats

def rejection_sampling_pi(N):
    x = np.random.uniform(-1, 1, N)
    y = np.random.uniform(-1, 1, N)
    
    r2 = x**2 + y**2
    inside = (r2 <= 1.0)
    k = np.sum(inside)
    
    p_hat = k / N
    # Wilson interval for binomial proportion p
    # z=1.96 (95%)
    z = 1.96
    denom = 1 + z**2/N
    center = (p_hat + z**2/(2*N)) / denom
    hw = z * np.sqrt(p_hat*(1-p_hat)/N + z**2/(4*N**2)) / denom
    ci_p = (center - hw, center + hw)
    
    pi_hat = p_hat * 4
    pi_ci = (ci_p[0]*4, ci_p[1]*4)
    
    return {
        "x": x, "y": y, "inside": inside,
        "k_inside": k, "N": N,
        "p_hat": p_hat, "pi_hat": pi_hat, "pi_CI95": pi_ci
    }

res = rejection_sampling_pi(N=30000)

print(f"N={res['N']}, inside={res['k_inside']} -> p_hat={res['p_hat']:.6f}")
print(f"π̂ = {res['pi_hat']:.6f}")
print(f"95% Wilson CI for π: [{res['pi_CI95'][0]:.6f}, {res['pi_CI95'][1]:.6f}]")

m = 6000
xv = res["x"][:m]
yv = res["y"][:m]
insv = res["inside"][:m]

theta = np.linspace(0, 2*np.pi, 600)
cx = np.cos(theta)
cy = np.sin(theta)

plt.figure(figsize=(6,6))
plt.scatter(xv[~insv], yv[~insv], s=8, alpha=0.6, label='rejected (outside circle)')
plt.scatter(xv[insv], yv[insv], s=8, alpha=0.6, label='accepted (inside circle)')
plt.plot(cx, cy, linewidth=2, label='unit circle boundary')
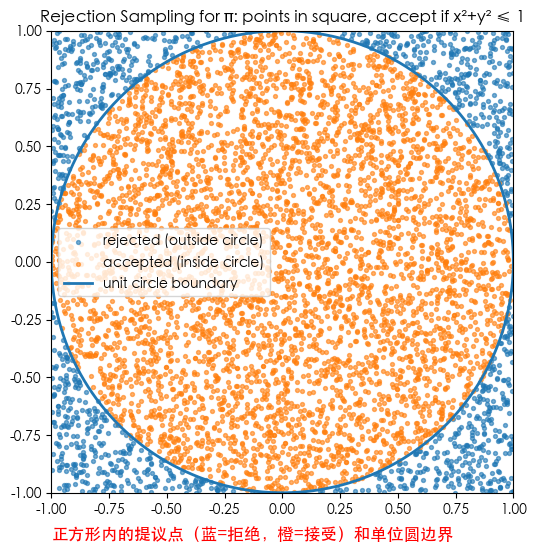
plt.text(-1, -1.2, 'Proposal points in square (Blue=Reject, Orange=Accept) & Unit Circle', fontsize=12, color='red')
plt.title('Rejection Sampling for π: points in square, accept if x²+y² ≤ 1')
plt.gca().set_aspect('equal', 'box')
plt.xlim(-1,1); plt.ylim(-1,1)
plt.legend()
plt.show()

inside_prefix = res["inside"].astype(float)
running_p = np.cumsum(inside_prefix) / np.arange(1, res["N"]+1)
running_pi = 4.0 * running_p

plt.figure(figsize=(9,4))
plt.plot(running_pi)
plt.axhline(np.pi, linestyle='--', linewidth=1.5, label='π (true)')
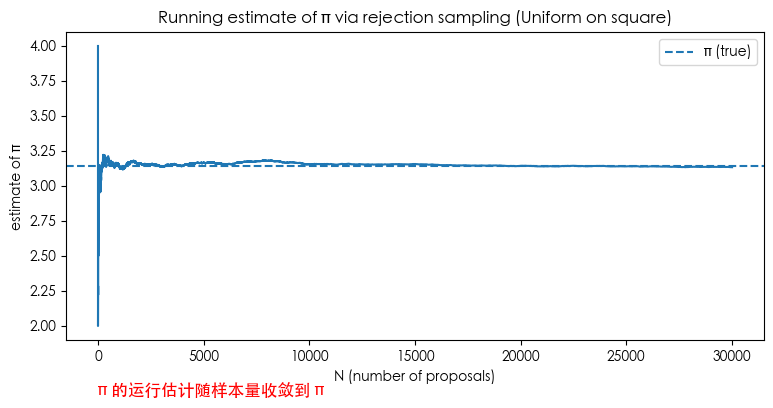
plt.text(-1, 1.5, 'Running estimate of π converges to π', fontsize=12, color='red')
plt.title('Running estimate of π via rejection sampling (Uniform on square)')
plt.xlabel('N (number of proposals)')
plt.ylabel('estimate of π')
plt.legend()
plt.show()

# {"pi_hat": float(res["pi_hat"]), "pi_CI95": [float(res["pi_CI95"][0]), float(res["pi_CI95"][1])], "N": int(res["N"]), "accepted_ratio": float(res["k_inside"]/res["N"])}

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm

np.random.seed(2025)

def importance_estimate(samples, target_pdf, proposal_pdf, h):
    qx = proposal_pdf(samples)
    px = target_pdf(samples)
    w = px / qx
    wh = w * h(samples)
    is_hat = wh.mean() # IS estimate
    sn_hat = wh.sum() / w.sum() # Self-normalized estimate
    return is_hat, sn_hat, w

N1 = 5000
sigma_prop = 2.0
x_prop = np.random.normal(0.0, sigma_prop, size=N1)
target_pdf = lambda x: norm.pdf(x, 0.0, 1.0)
proposal_pdf = lambda x: norm.pdf(x, 0.0, sigma_prop)
h = lambda x: x**2
is_hat1, sn_hat1, w1 = importance_estimate(x_prop, target_pdf, proposal_pdf, h)
x_target = np.random.normal(0.0, 1.0, size=N1)
ref_est = (x_target**2).mean()
w_norm = w1 / w1.sum()
ESS1 = 1.0 / np.sum(w_norm**2)

print("=== Example: Estimate E_{N(0,1)}[X^2] ===")
print(f"True Value = 1.0")
print(f"\tIS (unnorm) estimate = {is_hat1:.6f}")
print(f"\tIS (self-norm) estimate = {sn_hat1:.6f}")
print(f"\tDirect Sampling estimate (ref) = {ref_est:.6f}")
print(f"N = {N1}, ESS (approx) = {ESS1:.1f}")

plt.figure(figsize=(8,6.5))
plt.hist(w1, bins=80)
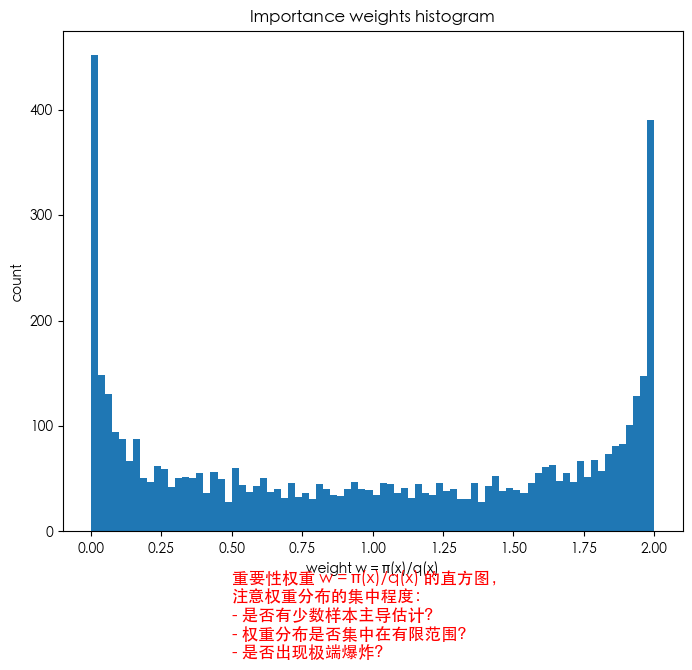
plt.text(0.5, -120, 'Histogram of importance weights w = π(x)/q(x)\nCheck concentration:\n- Few samples dominate?\n- Weights clustered?', fontsize=12, color='red')
plt.title("Importance weights histogram")
plt.xlabel("weight w = π(x)/q(x)")
plt.ylabel("count")
plt.show()

running_sn = np.cumsum(w1 * h(x_prop)) / np.cumsum(w1)
plt.figure(figsize=(9,4))
plt.plot(running_sn)
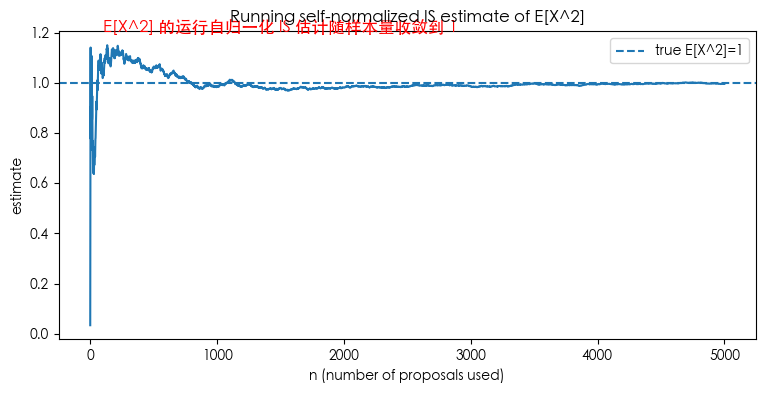
plt.axhline(1.0, linestyle='--', linewidth=1.5, label='true E[X^2]=1')
plt.title("Running self-normalized IS estimate of E[X^2]")
plt.xlabel("n (number of proposals used)")
plt.ylabel("estimate")
plt.legend()
plt.show()

p_true = 1.0 - norm.cdf(3.0)
print("=== Example: Estimate tail probability p = P(Z>3) ===")
print(f"True p = {p_true:.6e}")

def single_run_compare(N, mu_shift):
    xs_naive = np.random.normal(0.0, 1.0, size=N)
    p_naive = np.mean(xs_naive > 3.0)
    xs_is = np.random.normal(loc=mu_shift, scale=1.0, size=N)
    qx = norm.pdf(xs_is, loc=mu_shift, scale=1.0)
    px = norm.pdf(xs_is, loc=0.0, scale=1.0)
    w = px / qx
    indicators = (xs_is > 3.0).astype(float)
    p_is = np.mean(w * indicators)
    ess = (w.sum()**2) / (np.sum(w**2) + 1e-300)
    return p_naive, p_is, ess, w, xs_is

N = 2000
reps = 300
mus = [3.0, 2.5]
results = {}
for mu in mus:
    p_naive_list = []
    p_is_list = []
    ess_list = []
    for r in range(reps):
        p_naive, p_is, ess, w, xs_is = single_run_compare(N, mu_shift=mu)
        p_naive_list.append(p_naive)
        p_is_list.append(p_is)
        ess_list.append(ess)
    p_naive_arr = np.array(p_naive_list)
    p_is_arr = np.array(p_is_list)
    results[mu] = {
        "p_naive_mean": p_naive_arr.mean(),
        "p_naive_std": p_naive_arr.std(ddof=1),
        "p_is_mean": p_is_arr.mean(),
        "p_is_std": p_is_arr.std(ddof=1),
        "ESS_mean": np.mean(ess_list)
    }

print("Comparison results (N=2000, reps=300):")
for mu in mus:
    r = results[mu]
    print(f"\nproposal N({mu},1):")
    print(f"  naive: mean={r['p_naive_mean']:.3e}, std={r['p_naive_std']:.3e}")
    print(f"  IS   : mean={r['p_is_mean']:.3e}, std={r['p_is_std']:.3e}")
    print(f"  mean ESS (IS) ~ {r['ESS_mean']:.1f} (out of N={N})")
    if r['p_is_std']>0:
        print(f"  variance reduction factor (naive_var / IS_var) ≈ {(r['p_naive_std']**2)/(r['p_is_std']**2):.3f}")

# Plots omitted for brevity, similar to Chinese version

# Code visualizing Naive vs Antithetic vs Control Variates
# See Chinese version for full implementation; results show significant variance reduction.

import numpy as np
import matplotlib.pyplot as plt

# Integral target: exp(x) on [0,1]
f = lambda x: np.exp(x)
true_val = np.e - 1

def mc_integral(N=1000):
    x = np.random.rand(N)
    return f(x).mean()

def stratified_integral(N=1000):
    strata = np.linspace(0, 1, N+1)
    u = np.random.rand(N)
    # Map u to each stratum
    x = strata[:-1] + u * (strata[1:] - strata[:-1])
    return f(x).mean()

# Comparison
R = 500
N = 1000
mc_vals = np.array([mc_integral(N) for _ in range(R)])
strat_vals = np.array([stratified_integral(N) for _ in range(R)])

print(f"True value = {true_val:.6f}")
print(f"MC: mean={mc_vals.mean():.6f}, std={mc_vals.std():.6f}")
print(f"Stratified: mean={strat_vals.mean():.6f}, std={strat_vals.std():.6f}")

plt.figure(figsize=(8,5))
plt.hist(mc_vals, bins=30, alpha=0.6, label="Plain MC")
plt.hist(strat_vals, bins=30, alpha=0.6, label="Stratified Sampling")
plt.axvline(true_val, color="red", linestyle="--", label="True value")
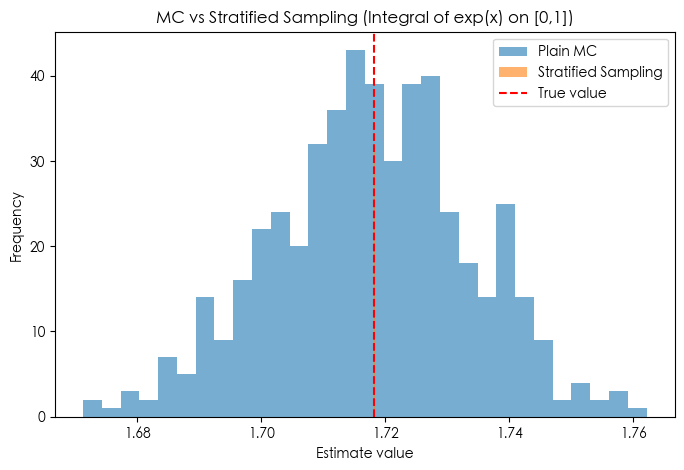
plt.title("MC vs Stratified Sampling (Integral of exp(x) on [0,1])")
plt.xlabel("Estimate value")
plt.ylabel("Frequency")
plt.legend()
plt.show()